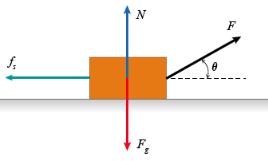
Two-dimensional dynamics often involves solving for two unknown quantities in two separate equations describing the total force. The block in (Figure 1) has a mass m = 10kg and is being pulled by a force F on a table with a coefficient of static friction μs = 0.3 Four forces act on it:

The applied force F (directed θ = 30 ^∘ above the horizontal).

The force of gravity Fg=mg (directly down, where g = 9.8m/s ² ).

The normal force N (directly up).

The force of static friction fs (directly left, opposing any potential motion).

If we want to find the size of the force necessary to just barely overcome static friction (in which case fs=μsN), we use the condition that the sum of the forces in both directions must be 0. Using some basic trigonometry, we can write this condition out for the forces in both the horizontal and vertical directions, respectively, as:

Fcosθ − μsN = 0

Fsinθ + N − mg = 0

In order to find the magnitude of force F, we have to solve a system of two equations with both F and the normal force N unknown. Use the methods we have learned to find an expression for F in terms of m, g, θ, and μs (no N).

F.