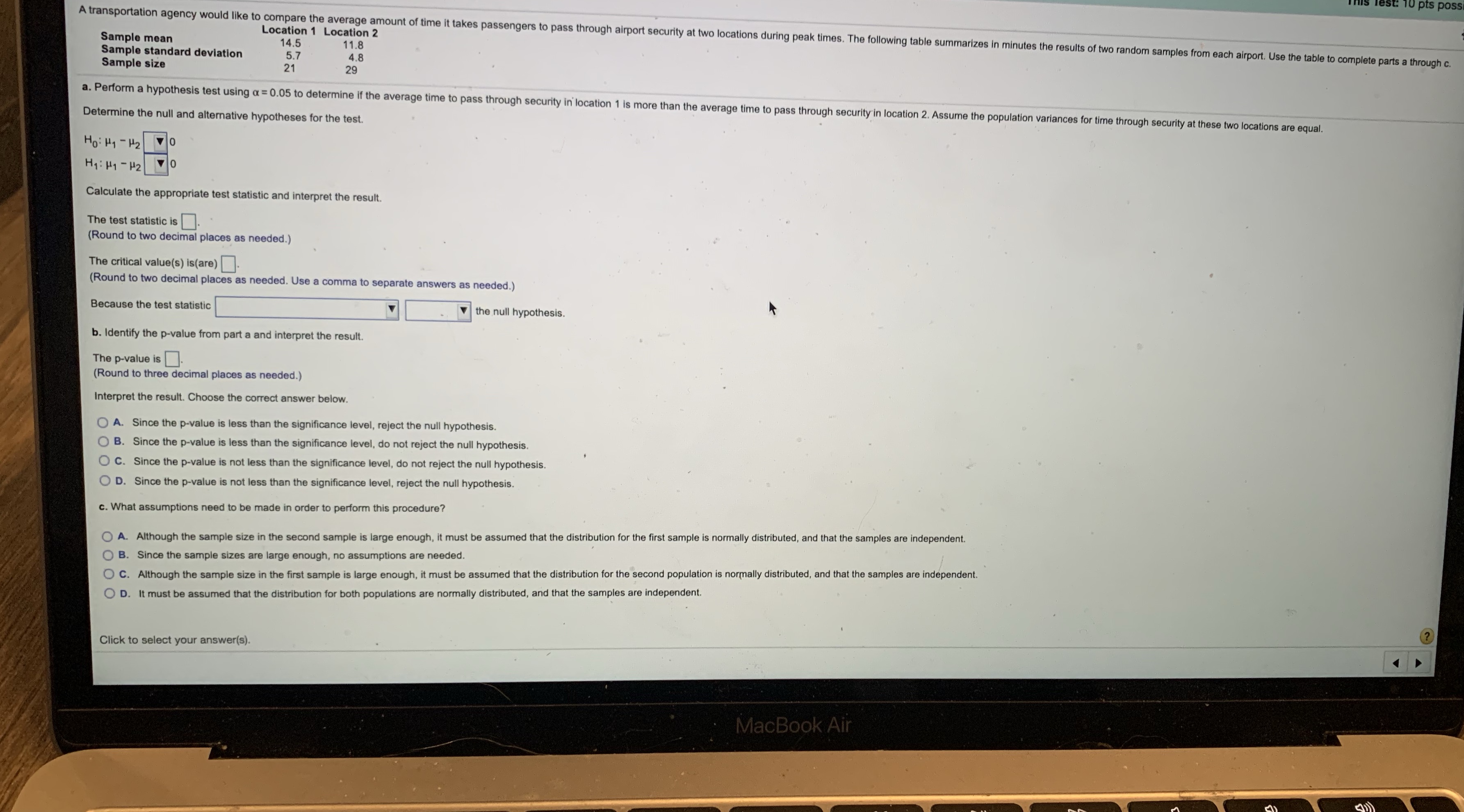
U pts poss Location 1 Location 2 A transportation agency would like to compare the average amount of time it takes passengers to pass through airport security at two locations during peak times. The following table summarizes in minutes the results of two random samples from each airport. Use the table to complete parts a through c. Sample mean 14.5 11.8 Sample standard deviation 5.7 4.8 Sample size 21 29 a. Perform a hypothesis test using a = 0.05 to determine if the average time to pass through security in location 1 is more than the average time to pass through security in location 2. Assume the population variances for time through security at these two locations are equal. Determine the null and alternative hypotheses for the test. HO : Hy - H2 VO Hy : H1 - H2 VO Calculate the appropriate test statistic and interpret the result. The test statistic is. (Round to two decimal places as needed.) The critical value(s) is(are). (Round to two decimal places as needed. Use a comma to separate answers as needed.) Because the test statistic V the null hypothesis. b. Identify the p-value from part a and interpret the result. The p-value is. (Round to three decimal places as needed.) Interpret the result. Choose the correct answer below. O A. Since the p-value is less than the significance level, reject the null hypothesis. O B. Since the p-value is less than the significance level, do not reject the null hypothesis. O C. Since the p-value is not less than the significance level, do not reject the null hypothesis. O D. Since the p-value is not less than the significance level, reject the null hypothesis. c. What assumptions need to be made in order to perform this procedure? O A. Although the sample size in the second sample is large enough, it must be assumed that the distribution for the first sample is normally distributed, and that the samples are independent. O B. Since the sample sizes are large enough, no assumptions are needed. O C. Although the sample size in the first sample is large enough, it must be assumed that the distribution for the second population is normally distributed, and that the samples are independent. O D. It must be assumed that the distribution for both populations are normally distributed, and that the samples are independent. ? Click to select your answer(s). MacBook Air