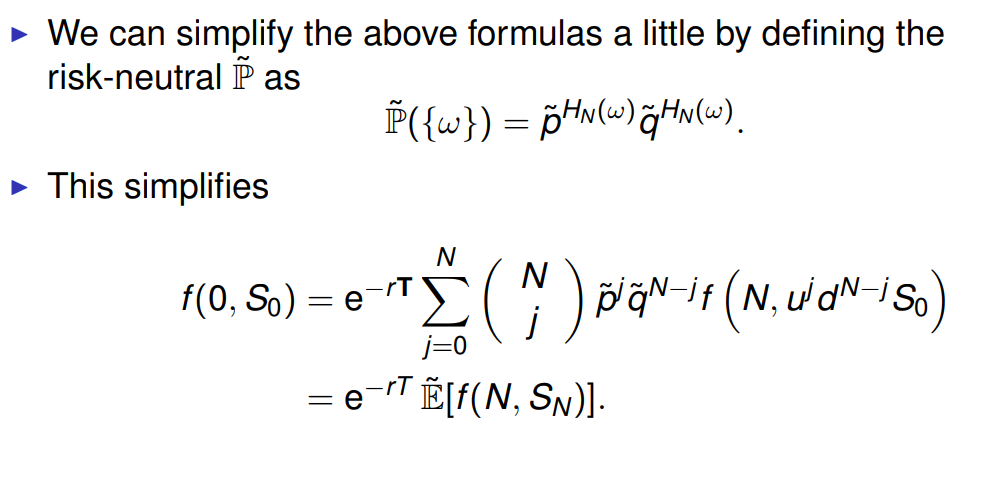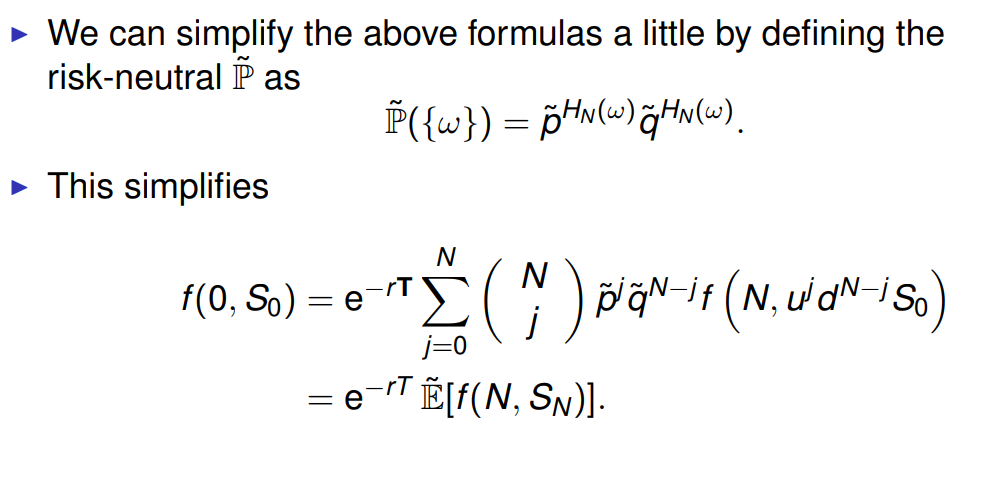


u-erat u-d. u-d 1 Let p= erat -d = 1 - = 1. The prices of the contingent claim on the tree are given by f(H) = e-rat [pfz(HH) + f2(HT)], f(T) = e [pfz(HT) + f2(TT)], fo = e-rat [pf1(H) +f(T)]. -r 2. The replicating portfolio of the contingent claim: = f2(HH) f2(HT) 1 f2(HH) f2(HT) A1(H) = S2(HH) S2(HT) uso u d f2(HT) f2(TT) 1 f2(HT) f2(TT) 41(T) = S2(HT) S2(TT) dSo u- d f4(H) f(T) 1 f1(H) f(T) = Si(H) S(T) So u d 21(H) =e-rat ufz(HT) dfz(HH) u d 41(T) = e-rat ufz(TT) dfz(HT) 9 u - d ?, Xo = e-rat ufy (T) dfy (H) u d Theorem Let the payoff of the contingent claim with maturity at period N be given as a function of stock price f(N, Sn). Then its no arbitrage price in a N-period recombinant binomial model is N N e @N-14 (N, WdN-iso) j=0 We can simplify the above formulas a little by defining the risk-neutral as P({w}) = Hr(w)Hn(w). This simplifies N f(0,5) = er n=18 (N, WON=iSo ) j=0 e- E[f(N, SN)]. As part of the multi-period binomial model, we have also shown that f(1, uSo) = e-r(N-1)AT E (^; - " ) rn-1-74 (N, Wqw-t-luso) More generally f(n, Sn(w1..wn)) = e-'(N-NAT N-n L (^; ")@gm-n-1 (N, Wqw-n-i Solw.n) Problem 1. This problem concerns the pricing of a European option in a two-period multiplicative binomial tree market. Suppose the present stock price is So = 50, the time interval is AT = 0.5 years, and the multiplicative factors are u = 1.2, d=0.8 (so the stock price 0.5 years from now is either uS, or dSo, and the stock price 1 year from now is either u-So, udSo, or dSo). Assume the risk-free rate is constant and is 4% per year. a) Find the no arbitrage price of a European put with strike 45 and maturity 1 year. b) Verify that the formula derived in class for the price of a derivative security in a general N-period tree matches the price from part a). c) Describe the trading strategy that replicates this option, using stock and the risk-free bond. u-erat u-d. u-d 1 Let p= erat -d = 1 - = 1. The prices of the contingent claim on the tree are given by f(H) = e-rat [pfz(HH) + f2(HT)], f(T) = e [pfz(HT) + f2(TT)], fo = e-rat [pf1(H) +f(T)]. -r 2. The replicating portfolio of the contingent claim: = f2(HH) f2(HT) 1 f2(HH) f2(HT) A1(H) = S2(HH) S2(HT) uso u d f2(HT) f2(TT) 1 f2(HT) f2(TT) 41(T) = S2(HT) S2(TT) dSo u- d f4(H) f(T) 1 f1(H) f(T) = Si(H) S(T) So u d 21(H) =e-rat ufz(HT) dfz(HH) u d 41(T) = e-rat ufz(TT) dfz(HT) 9 u - d ?, Xo = e-rat ufy (T) dfy (H) u d Theorem Let the payoff of the contingent claim with maturity at period N be given as a function of stock price f(N, Sn). Then its no arbitrage price in a N-period recombinant binomial model is N N e @N-14 (N, WdN-iso) j=0 We can simplify the above formulas a little by defining the risk-neutral as P({w}) = Hr(w)Hn(w). This simplifies N f(0,5) = er n=18 (N, WON=iSo ) j=0 e- E[f(N, SN)]. As part of the multi-period binomial model, we have also shown that f(1, uSo) = e-r(N-1)AT E (^; - " ) rn-1-74 (N, Wqw-t-luso) More generally f(n, Sn(w1..wn)) = e-'(N-NAT N-n L (^; ")@gm-n-1 (N, Wqw-n-i Solw.n) Problem 1. This problem concerns the pricing of a European option in a two-period multiplicative binomial tree market. Suppose the present stock price is So = 50, the time interval is AT = 0.5 years, and the multiplicative factors are u = 1.2, d=0.8 (so the stock price 0.5 years from now is either uS, or dSo, and the stock price 1 year from now is either u-So, udSo, or dSo). Assume the risk-free rate is constant and is 4% per year. a) Find the no arbitrage price of a European put with strike 45 and maturity 1 year. b) Verify that the formula derived in class for the price of a derivative security in a general N-period tree matches the price from part a). c) Describe the trading strategy that replicates this option, using stock and the risk-free bond