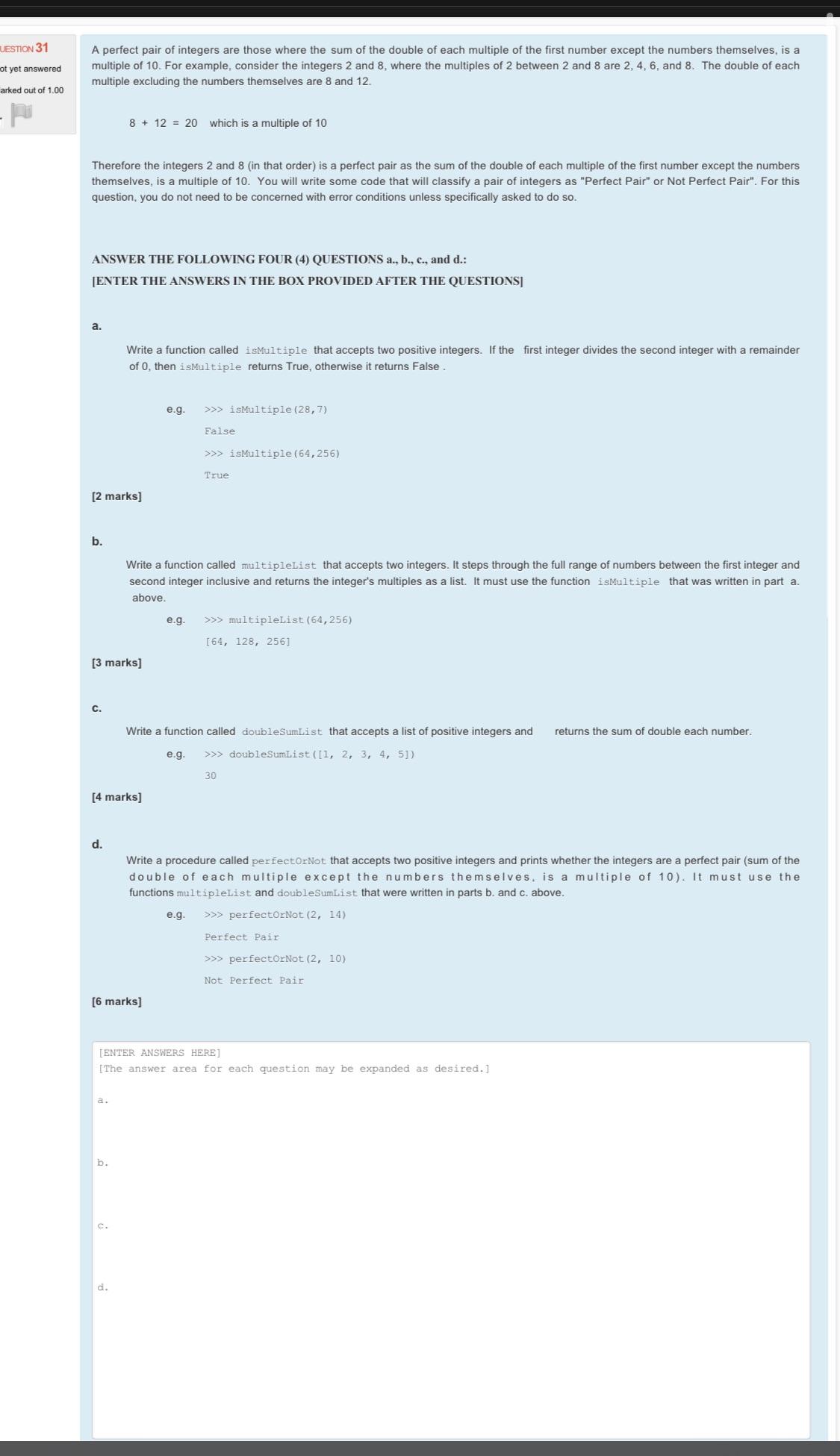
UESTION 31 ot yet answered arked out of 1.00 A perfect pair of integers are those where the sum of the double of each multiple of the first number except the numbers themselves, is a multiple of 10. For example, consider the integers 2 and 8, where the multiples of 2 between 2 and 8 are 2, 4, 6, and 8. The double of each multiple excluding the numbers themselves are 8 and 12. - 81220 which is a multiple of 10 Therefore the integers 2 and 8 (in that order) is a perfect pair as the sum of the double of each multiple of the first number except the numbers themselves, is a multiple of 10. You will write some code that will classify a pair of integers as "Perfect Pair" or Not Perfect Pair". For this question, you do not need to be concerned with error conditions unless specifically asked to do so. ANSWER THE FOLLOWING FOUR (4) QUESTIONS a., b., c., and d.: [ENTER THE ANSWERS IN THE BOX PROVIDED AFTER THE QUESTIONS] a. Write a function called isMultiple that accepts two positive integers. If the first integer divides the second integer with a remainder of 0, then isMultiple returns True, otherwise it returns False. [2 marks] e.g. >>> isMultiple (28,7) False >>> isMultiple (64,256) True b. Write a function called multipleList that accepts two integers. It steps through the full range of numbers between the first integer and second integer inclusive and returns the integer's multiples as a list. It must use the function isMultiple that was written in part a. above. e.g. >>> multipleList (64,256) [3 marks] C. [64, 128, 256] Write a function called doubleSumList that accepts a list of positive integers and [4 marks] d. e.g. >>> doubleSumList ([1, 2, 3, 4, 5]) 30 returns the sum of double each number. Write a procedure called perfectOrNot that accepts two positive integers and prints whether the integers are a perfect pair (sum of the double of each multiple except the numbers themselves, is a multiple of 10). It must use the functions multipleList and doubleSumList that were written in parts b. and c. above. e.g. >>> perfectOrNot (2, 14) Perfect Pair >>> perfectOrNot (2, 10) Not Perfect Pair [6 marks] [ENTER ANSWERS HERE] [The answer area for each question may be expanded as desired.] a. b. d.