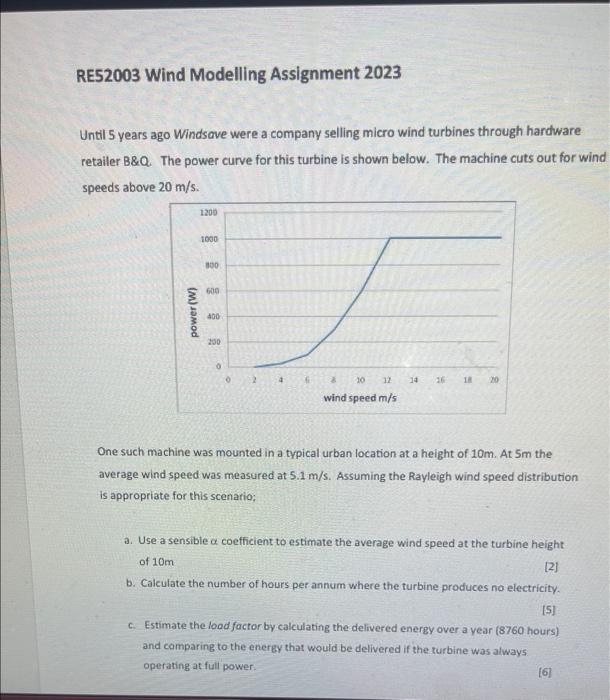
Until 5 years ago Windsave were a company selling micro wind turbines through hardware retailer B&Q. The power curve for this turbine is shown below. The machine cuts out for wind speeds above 20m/s. One such machine was mounted in a typical urban location at a height of 10m. At 5m the average wind speed was measured at 5.1m/s. Assuming the Rayleigh wind speed distribution is appropriate for this scenario; a. Use a sensible coefficient to estimate the average wind speed at the turbine height of 10m [2] b. Calculate the number of hours per annum where the turbine produces no electricity. [5] c. Estimate the lood factor by calculating the delivered energy over a year ( 8760 hours) and comparing to the enerey that would be delivered if the turbine was always operating at full power. [6] d. Estimate the return on investment over the expected lifetime of 15 years if the total outlay is 3500, and a feed in tariff of 34.5/kWh is payable. Assume a load factor of 0.13 (this might not agree with your calculated value), and a domestic electricity tariff of 16.0p/kWh. For small domestic turbines it is assumed (this is not metered) that 50% of RE42002 Wind and Marine Energy July 2022 generated electricity is consumed by the household, and 50% is exported to the grid. State clearly any other factors or assumptions made. [7] TOTAL =20 MARKS Rayleigh distribution function f(u)=2u2uexp[4(uu)2] Cumulative distribution function F(u)=1exp[4(uu)2] Where u is the wind speed, and u is the average wind speed at the turbine height. NOTES: 1. You will need to generate a table with a column for the wind speeds starting at 3m/s and incrementing in 1m/s steps to 20m/s. 2. You will next need a column with the calculated values of ffu) corresponding to each wind speed. 3. Since the analysis is over a calendar year you should take the f(u) values at each wind speed and multiply by 8760 hours to obtain values for the total energy generated (kW or MWh) at each wind speed. 4. Sum all of the values obtained in (3) to get the expected annual energy output 5. As a check that your f(u) values are consistent you should sum the entries obtained in (2) and make sure these add up to one. 6. In part (b) you should use the cumulative function F(u) to obtain the probabilities that the wind speed is either below the cut-in or above the cut-out values