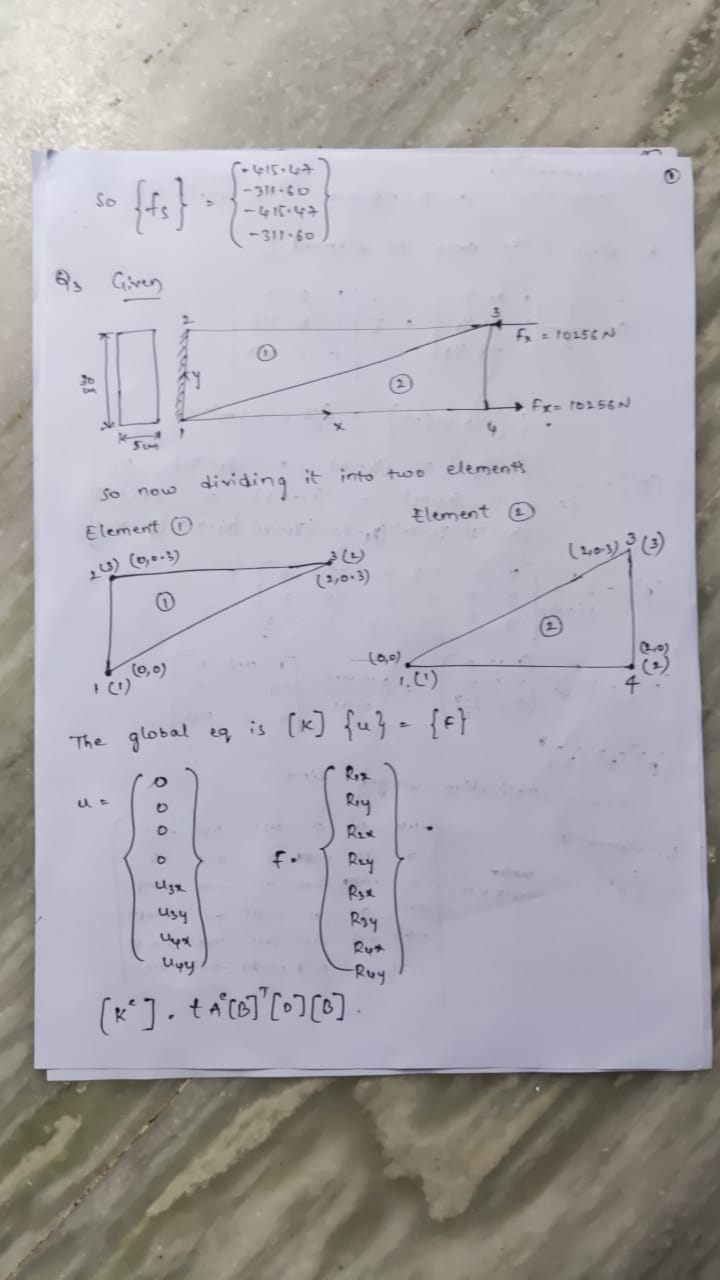
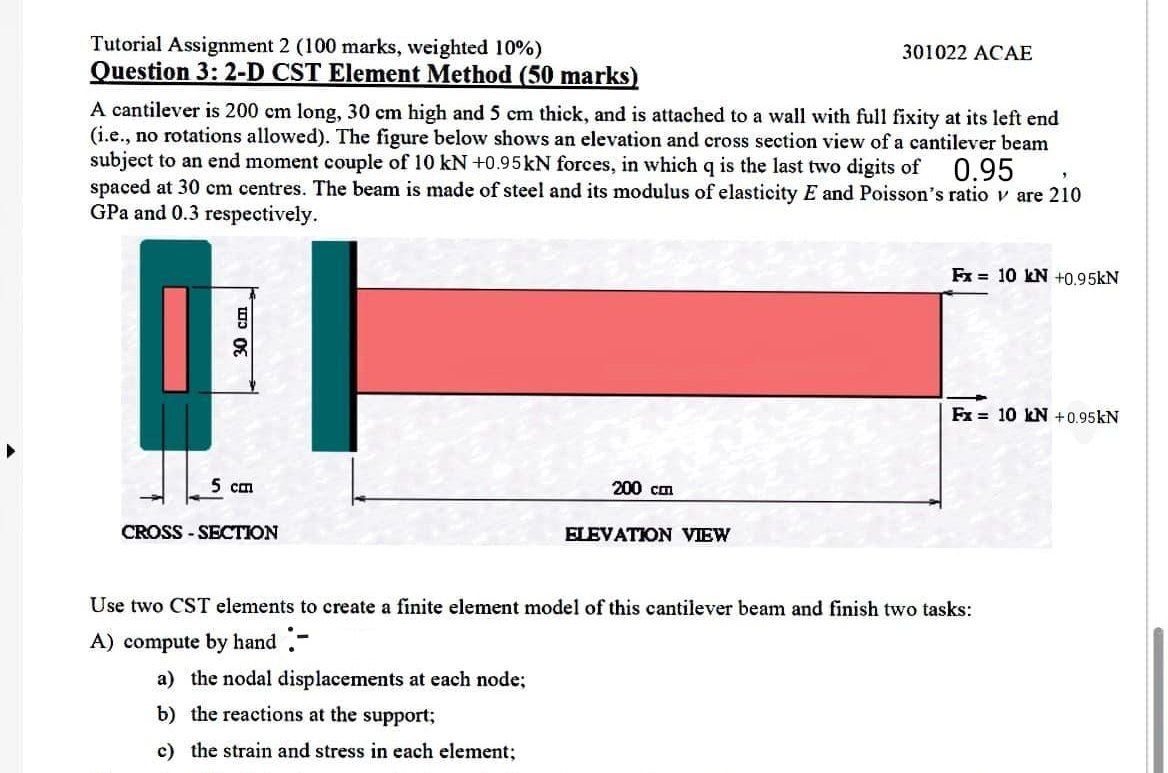
upon solving there equations in matrix form we get U gx = 144 43. 53 x 10, U zy = 9099. 46 * 107 4ux = 160#9. 25 X 10 Huy = 9906 . 006 x 10 7 m stresses in each element 3 for element 1 D JYL for stress in element 1 (4: 33 x 10- 14 1:19 * 10 -14 9:55x10-13 for element ?) upon calculation we get F4- 35 X 10#13 - 1.59 *10- 12 1 . 02 8 x 10 - /2\f- 4:15-64 so ffs ) -311-40 - 415.47 -311.60 2 , Given Fo = 10156N O (2 fx= 10156N 4 so now dividing it into two elements Element 1 Element 2 03 ) (0 , 0 -3 ) 3 ( 2 ) (403) 3 (3) ( 2/ 0. 3) 2 (0, 0) (0, 0 ) . 1. ( ") 4 The global eq is [ k) fu - for O U = 0 Rex Rey Ugx usy Rgy Rut upy Ruy ( * ' ] . t ACB] [ .] [B ]so for element 1 ( 24 , , 4, ) = 10, 0) ( 312, 42 ) = ( 2, 0. 3) (x3, 4, ) = (0, 0.3) for Area of element " A = M1 2 42= 2 1 ( 03) ( 2) ] = 0.3 m2 (B] . ( 4 1- 4 , ) 0 ( 43 - 4, ) ( 4 ,- 4 2 ) 0 ( X , - 34 ) ( * *3-312) (42-43) (x,-M3) (43- 4.) (#2-2:) (4,-42) ( B ] 0:3 - 0 + 3 6 . 6 - 1 2 0: 3 -013 ( D ] . - 210 * 10 D. 3 D.5 0:91 D D 0. 35 so for element stiffness matrix. 1.4 - 1 +4 10.2 D D 8+18 [K ( ] : 9.615 * 10 -0:18 0109 -0+ 09 6:18 - 0:21 O 0:0315 01 21-0.0315 -1:4 0.18 -0109 0.49 -0.39 -610315-0.39 4:0315 for element ( 2 ) ( X 1 , 4 . ) = (0. 0) ( 2 2, 42 ) = (210) 123, 43/ ( 2, 0.3) Area up on solving we get 013 mTutorial Assignment 2 (100 marks, weighted 10%) 301022 ACAE Question 3: 2-D CST Element Method (50 marks) A cantilever is 200 cm long, 30 cm high and 5 cm thick, and is attached to a wall with full fixity at its left end (i.e., no rotations allowed). The figure below shows an elevation and cross section view of a cantilever beam subject to an end moment couple of 10 kN +0.95kN forces, in which q is the last two digits of 0.95 spaced at 30 cm centres. The beam is made of steel and its modulus of elasticity E and Poisson's ratio v are 210 GPa and 0.3 respectively. Fx = 10 kN +0.95kN 30 cm Fx = 10 KN +0.95kN 5 cm 200 cm CROSS - SECTION ELEVATION VIEW Use two CST elements to create a finite element model of this cantilever beam and finish two tasks: A) compute by hand - a) the nodal displacements at each node; b) the reactions at the support; c) the strain and stress in each element