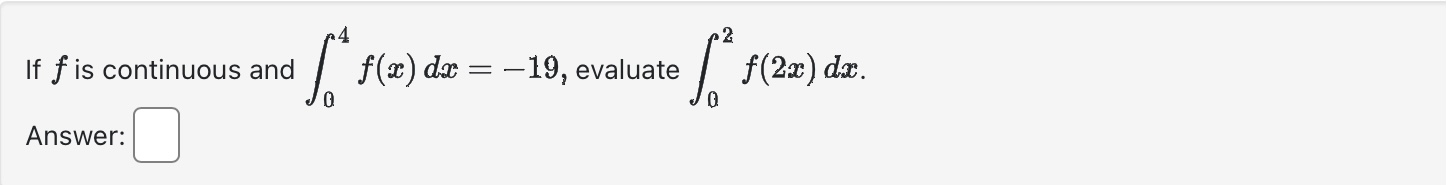
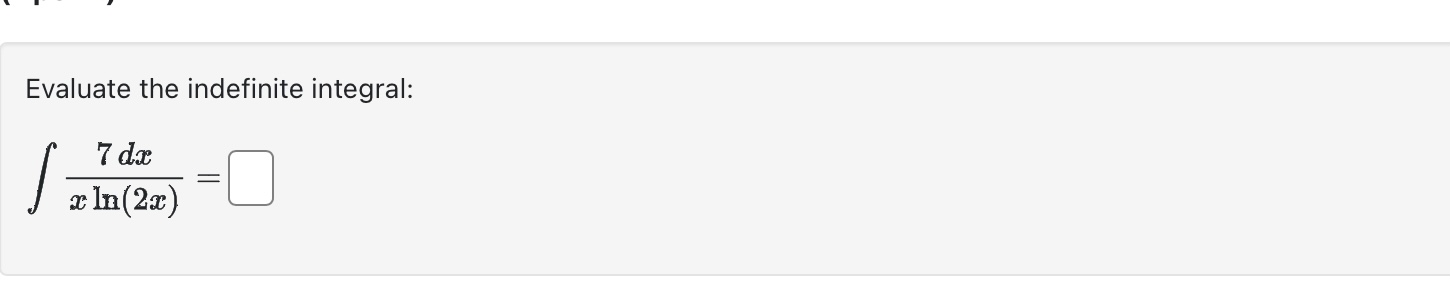
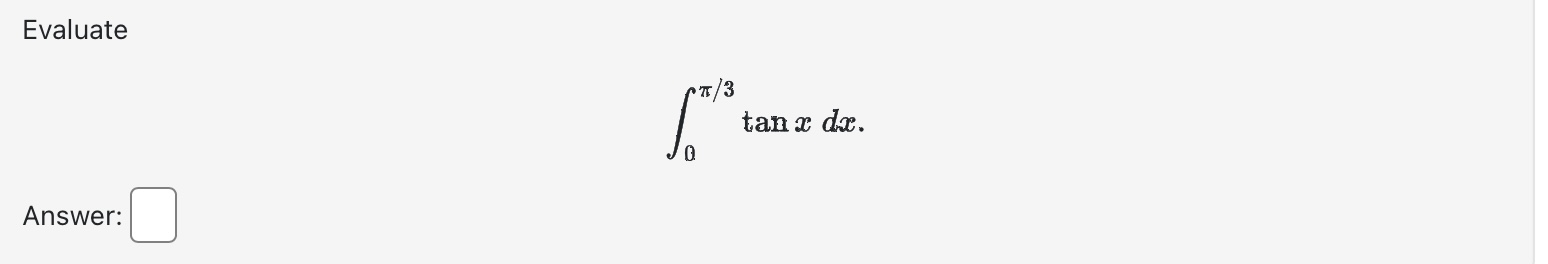
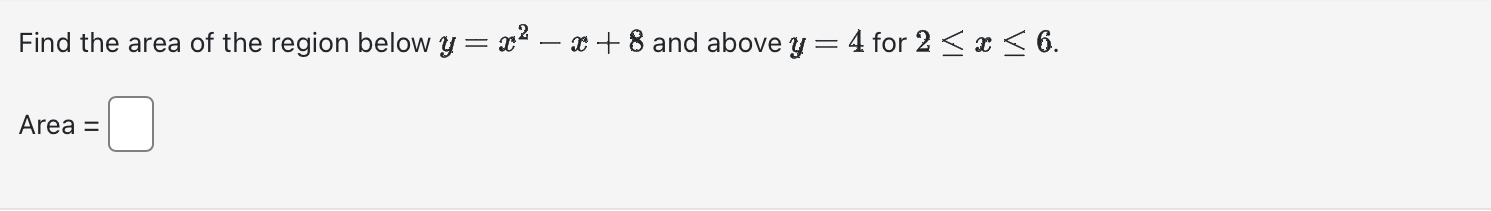
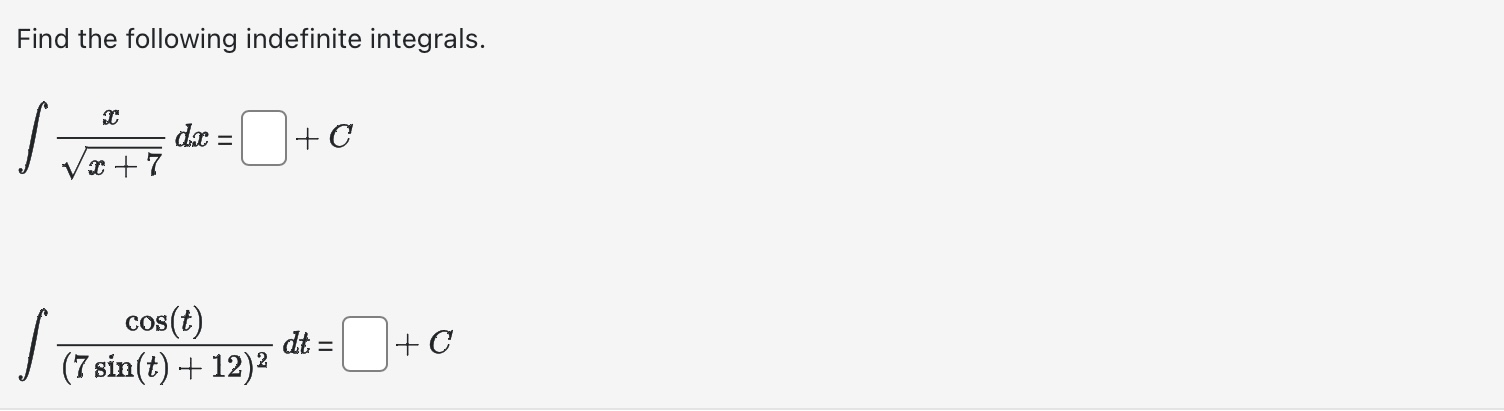
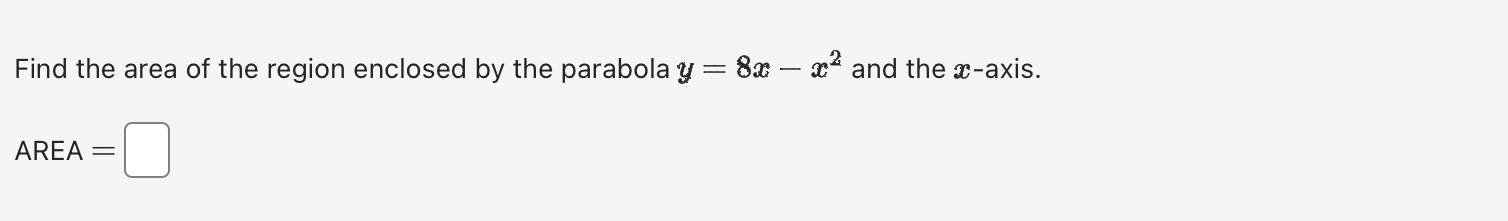
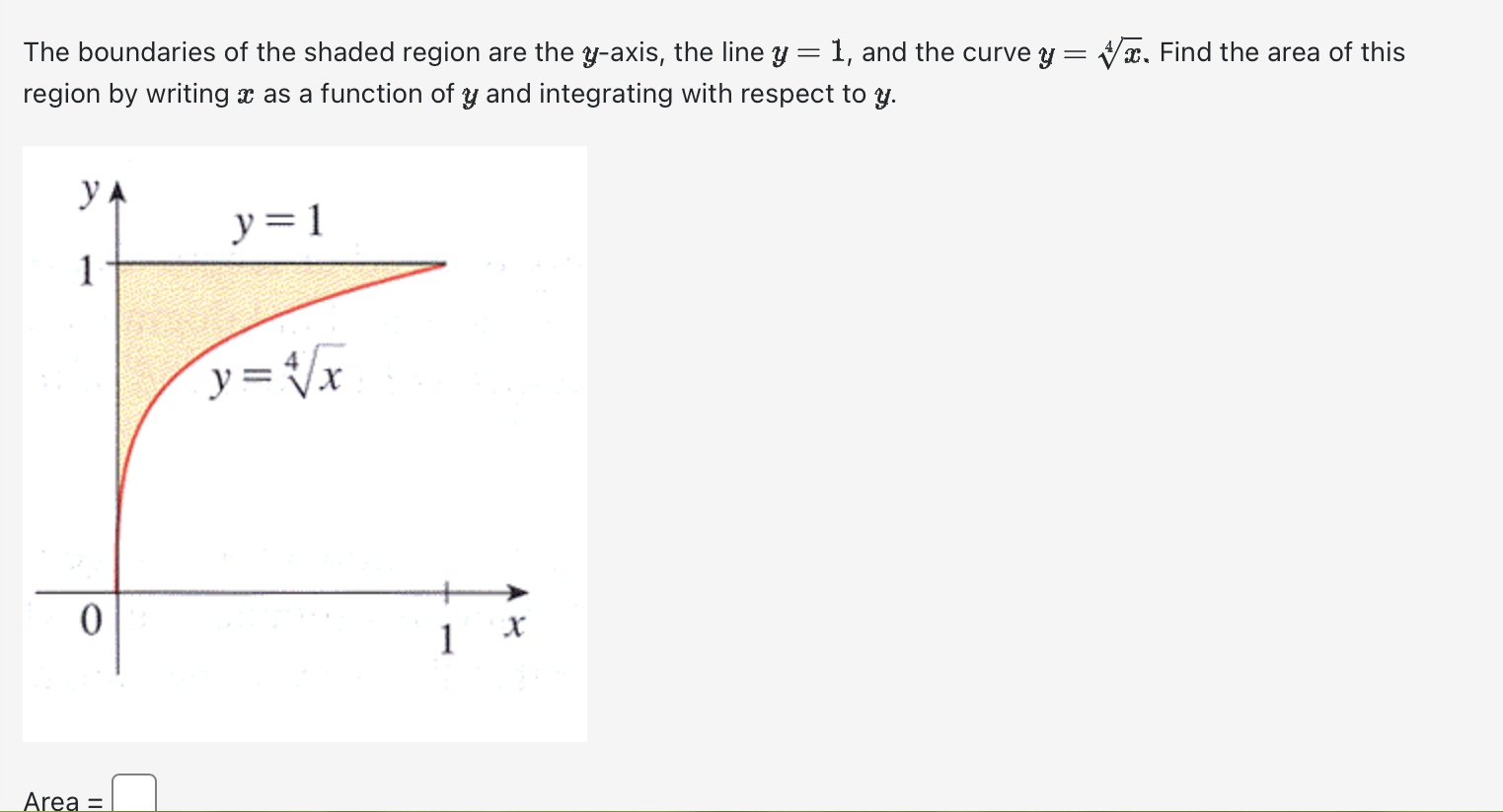
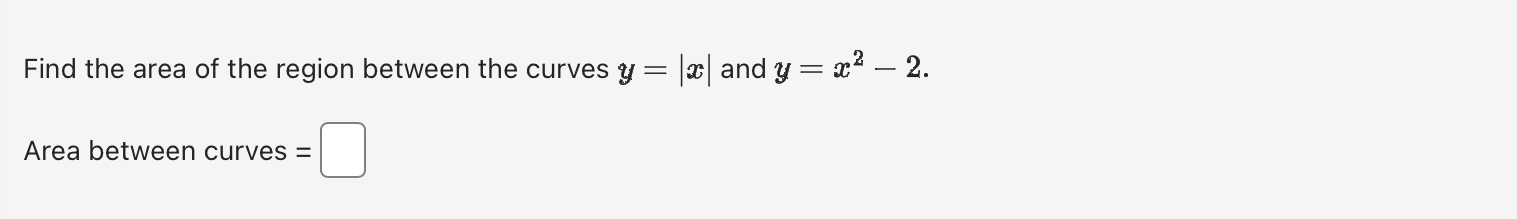
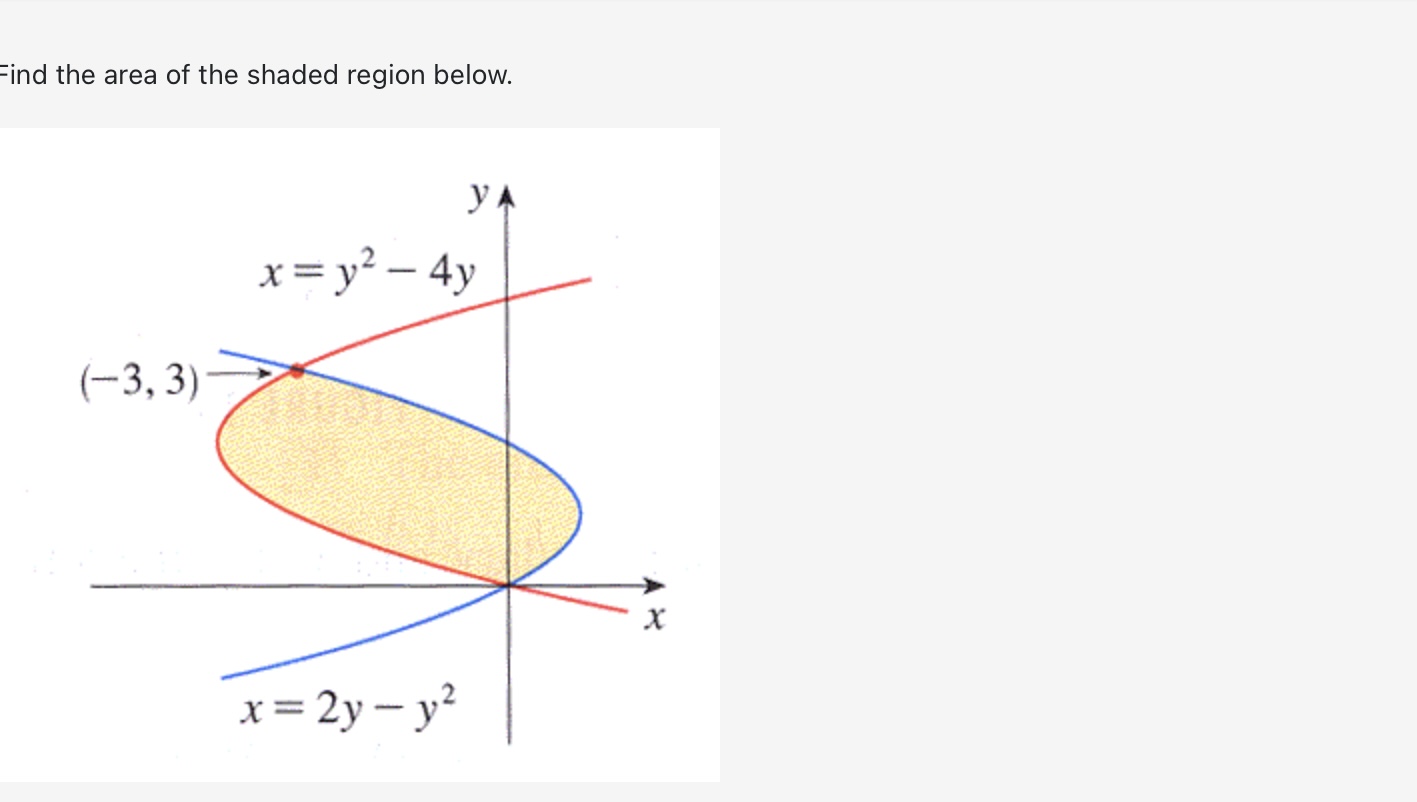
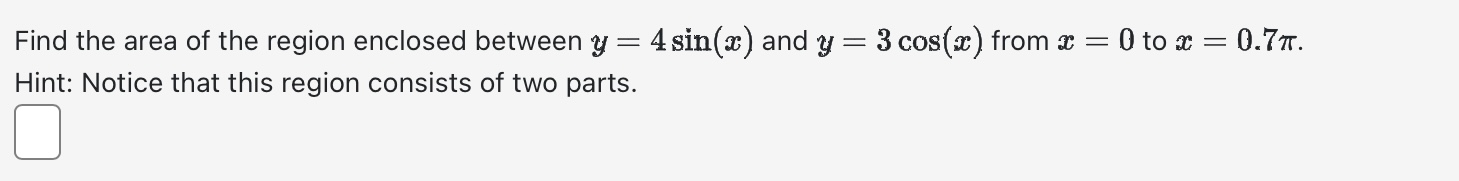
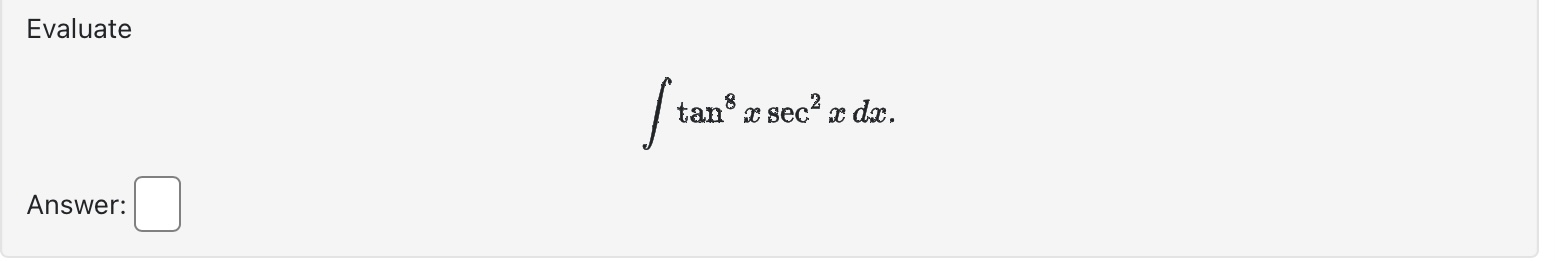
Use calculus to find the area of the triangle with the vertices (0, 5), (2, -2), and (5, 1). Area between curves = Evaluate the integral using an appropriate substitution. r8+1 r9 + 9r dx =+c Evaluate the integral using an appropriate substitution. sin (-5) 4x S dx 0+ + C Evaluate the definite integral: 1 2-5 da=0 2e8t dx e 4x If f is continuous and Answer: [*f(x) dr = -19, evaluate 2 f* f(2x) dx. Evaluate the indefinite integral: 7 dx / x In (2x) Evaluate Answer: 0. T/3 tan x dx. Find the area of the region below y = x - x + 8 and above y = 4 for 2 < x < 6. Area = Find the following indefinite integrals. +0 dx = x + 7 | cos(t) (7 sin(t) + 12) + C = 0 +c dt = Find the area of the region enclosed by the parabola y - AREA = 8 and the x-axis. Evaluate the integral (by interpreting it as the area between two curves) 4 S|VZ|2 x + 2 0 x dx Evaluate the definite integral. P/2 -/2 sin(x) cos(x) dx = = The boundaries of the shaded region are the y-axis, the line y = 1, and the curve y region by writing a as a function of y and integrating with respect to y. 1 0 Area = y = 1 y = 4/x 1 . Find the area of this Find the area of the region between the curves y = || and y = x 2. Area between curves = Find the area of the shaded region below. (-3,3) x = y - 4y x=2y-y X Evaluate the integral | 6 cot (2) In(sin(2)) da Note: Use an upper-case "C" for the constant of integration. Consider the area between the graphs x + y= 21 and x + 9 = y. This area can be computed in two different ways using integrals First of all it can be computed as a sum of two integrals where a = (x) = g(x) = = =0c=0 C - Alternatively this area can be computed as a single integral [ where a = h(y) Either way we find that the area is and and ["F(x) dx + ["0(1) de g(x) dx h(y) dy Evaluate the integral by any method. Lv xe 7x dx = Find the area of the region enclosed between y = 4 sin(x) and y = 3 cos(x) from x = = 0 to x= 0.7t. Hint: Notice that this region consists of two parts. Evaluate Answer: I tan x sec x dx. a