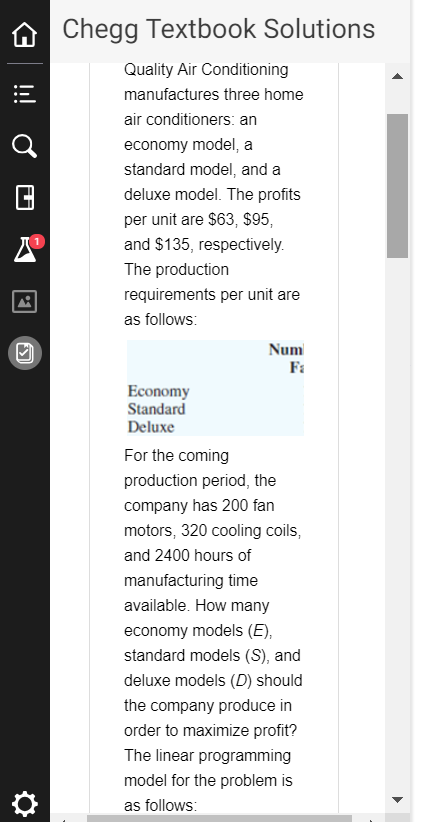
Use Excel, attach print-outs, explain answers

Use Excel, attach print-outs, explain answers

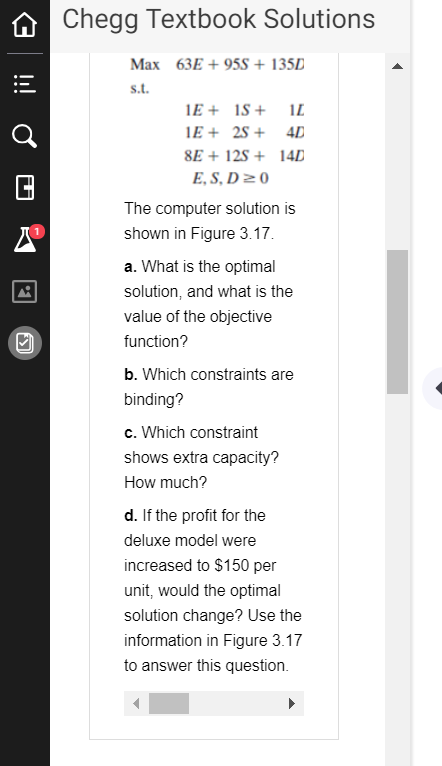
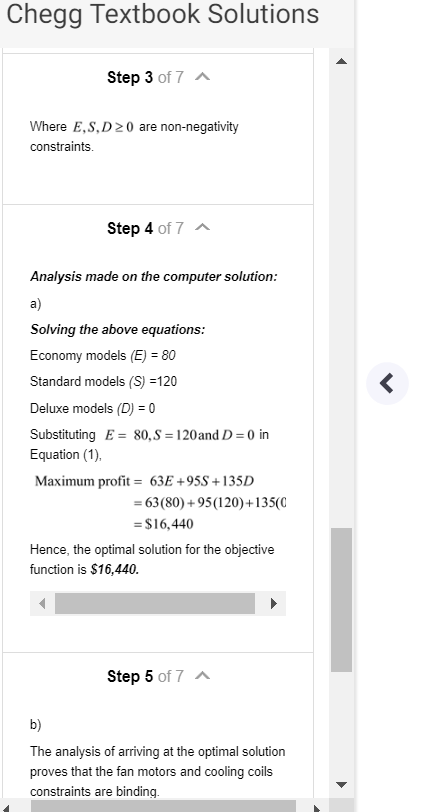
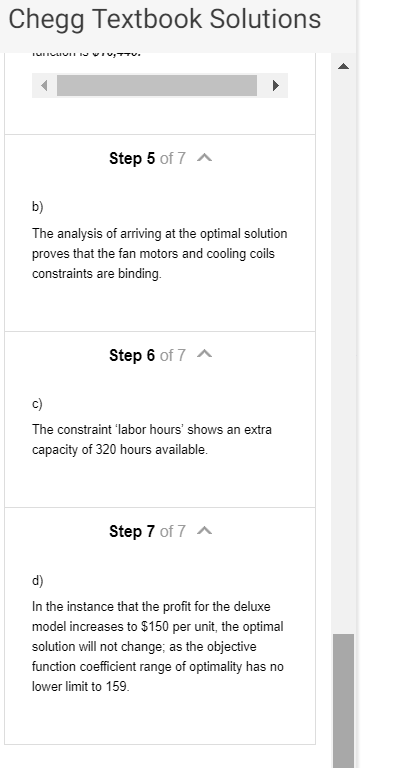
Chegg Textbook Solutions Quality Air Conditioning manufactures three home air conditioners: an economy model, a standard model, and a deluxe model. The profits per unit are $63, $95, and $135, respectively The production requirements per unit are as follows Num Economy Standard Deluxe For the coming production period, the company has 200 farn motors, 320 cooling coils and 2400 hours of manufacturing time available. How many economy models (E) standard models (S), and deluxe models (D) should the company produce in order to maximize profit? The linear programming model for the problem is as follows Chegg Textbook Solutions Max 63E +95S+135D s.t. ES+1 8E 12S14D E. S.D20 The computer solution is shown in Figure 3.17 a. What is the optimal solution, and what is the value of the objective function? b. Which constraints are binding? c. Which constraint shows extra capacity? How much? d. If the profit for the deluxe model were increased to $150 per unit, would the optimal solution change? Use the information in Figure 3.17 to answer this question Chegg Textbook Solutions Step 3 of 7 Where E,S,D20 are non-negativity constraints Step 4 of 7 Analysis made on the computer solution: a) Solving the above equations: Economy models (E)- Standard models (S)-120 Deluxe models (D)0 Substituting E-80,S 120and D-0 in Equation (1) Maximum profit- 63E+95S+135D 63(80+95(120)+135(0 = $ 16,440 Hence, the optimal solution for the objective function is $16,440. Step 5 of 7 b) The analysis of arriving at the optimal solution proves that the fan motors and cooling coils constraints are binding Chegg Textbook Solutions Step 5 of 7 b) The analysis of arriving at the optimal solution proves that the fan motors and cooling coils constraints are binding. Step 6 of 7 c) The constraint 'labor hours' shows an extra capacity of 320 hours available Step 7 of 7 d) In the instance that the profit for the deluxe model increases to $150 per unit, the optimal solution will not change; as the objective function coefficient range of optimality has no lower limit to 159 swer - iven -that max 63t953 t 135 D a) optima Soltion -the Objective unction, economy mde kie) so Standlard oodels (s - 12o Delene O 63080) +43sCo) tHence,-the optimal Solutian -or -the objacttve unction 16:440 he- proves the motos, coolino -times are not naiesis of arivin at the optima Solurtion tors , coolina cols, manufacturin ng manufacturing -im nor binding Fa motoss, coolingcos ae nen bi y and -there having no extra capaci tu manufacturng-time is or ndin and extra copocity 32o hours d) Th-the instance -that tha picfit -t the model 'incrases -to fi5o per unit the optimal Solution soin not hange as the objective unt Coefticient range f optimaliry has na wer to 159 allowable ocase u Chegg Textbook Solutions Quality Air Conditioning manufactures three home air conditioners: an economy model, a standard model, and a deluxe model. The profits per unit are $63, $95, and $135, respectively The production requirements per unit are as follows Num Economy Standard Deluxe For the coming production period, the company has 200 farn motors, 320 cooling coils and 2400 hours of manufacturing time available. How many economy models (E) standard models (S), and deluxe models (D) should the company produce in order to maximize profit? The linear programming model for the problem is as follows Chegg Textbook Solutions Max 63E +95S+135D s.t. ES+1 8E 12S14D E. S.D20 The computer solution is shown in Figure 3.17 a. What is the optimal solution, and what is the value of the objective function? b. Which constraints are binding? c. Which constraint shows extra capacity? How much? d. If the profit for the deluxe model were increased to $150 per unit, would the optimal solution change? Use the information in Figure 3.17 to answer this question Chegg Textbook Solutions Step 3 of 7 Where E,S,D20 are non-negativity constraints Step 4 of 7 Analysis made on the computer solution: a) Solving the above equations: Economy models (E)- Standard models (S)-120 Deluxe models (D)0 Substituting E-80,S 120and D-0 in Equation (1) Maximum profit- 63E+95S+135D 63(80+95(120)+135(0 = $ 16,440 Hence, the optimal solution for the objective function is $16,440. Step 5 of 7 b) The analysis of arriving at the optimal solution proves that the fan motors and cooling coils constraints are binding Chegg Textbook Solutions Step 5 of 7 b) The analysis of arriving at the optimal solution proves that the fan motors and cooling coils constraints are binding. Step 6 of 7 c) The constraint 'labor hours' shows an extra capacity of 320 hours available Step 7 of 7 d) In the instance that the profit for the deluxe model increases to $150 per unit, the optimal solution will not change; as the objective function coefficient range of optimality has no lower limit to 159 swer - iven -that max 63t953 t 135 D a) optima Soltion -the Objective unction, economy mde kie) so Standlard oodels (s - 12o Delene O 63080) +43sCo) tHence,-the optimal Solutian -or -the objacttve unction 16:440 he- proves the motos, coolino -times are not naiesis of arivin at the optima Solurtion tors , coolina cols, manufacturin ng manufacturing -im nor binding Fa motoss, coolingcos ae nen bi y and -there having no extra capaci tu manufacturng-time is or ndin and extra copocity 32o hours d) Th-the instance -that tha picfit -t the model 'incrases -to fi5o per unit the optimal Solution soin not hange as the objective unt Coefticient range f optimaliry has na wer to 159 allowable ocase u