use java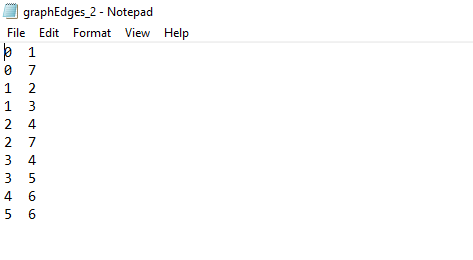

import java.io.*;

import java.util.*;

class Node{

private int data;

private Node nextNodePtr;

public Node(){}

public void setData(int d){

data = d;

}

public int getData(){

return data;

}

public void setNextNodePtr(Node nodePtr){

nextNodePtr = nodePtr;

}

public Node getNextNodePtr(){

return nextNodePtr;

}

}

class List{

private Node headPtr;

public List(){

headPtr = new Node();

headPtr.setNextNodePtr(null);

}

public Node getHeadPtr(){

return headPtr;

}

public boolean isEmpty(){

if (headPtr.getNextNodePtr() == null)

return true;

return false;

}

public void insert(int data){

Node currentNodePtr = headPtr.getNextNodePtr();

Node prevNodePtr = headPtr;

while (currentNodePtr != null){

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr.getNextNodePtr();

}

Node newNodePtr = new Node();

newNodePtr.setData(data);

newNodePtr.setNextNodePtr(null);

prevNodePtr.setNextNodePtr(newNodePtr);

}

public void insertAtIndex(int insertIndex, int data){

Node currentNodePtr = headPtr.getNextNodePtr();

Node prevNodePtr = headPtr;

int index = 0;

while (currentNodePtr != null){

if (index == insertIndex)

break;

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr.getNextNodePtr();

index++;

}

Node newNodePtr = new Node();

newNodePtr.setData(data);

newNodePtr.setNextNodePtr(currentNodePtr);

prevNodePtr.setNextNodePtr(newNodePtr);

}

public int read(int readIndex){

Node currentNodePtr = headPtr.getNextNodePtr();

Node prevNodePtr = headPtr;

int index = 0;

while (currentNodePtr != null){

if (index == readIndex)

return currentNodePtr.getData();

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr.getNextNodePtr();

index++;

}

return -1; // an invalid value indicating

// index is out of range

}

public void modifyElement(int modifyIndex, int data){

Node currentNodePtr = headPtr.getNextNodePtr();

Node prevNodePtr = headPtr;

int index = 0;

while (currentNodePtr != null){

if (index == modifyIndex){

currentNodePtr.setData(data);

return;

}

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr.getNextNodePtr();

index++;

}

}

public void deleteElementAtIndex(int deleteIndex){

Node currentNodePtr = headPtr.getNextNodePtr();

Node prevNodePtr = headPtr;

Node nextNodePtr = headPtr;

int index = 0;

while (currentNodePtr != null){

if (index == deleteIndex){

nextNodePtr = currentNodePtr.getNextNodePtr();

break;

}

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr.getNextNodePtr();

index++;

}

prevNodePtr.setNextNodePtr(nextNodePtr);

}

public void deleteElement(int deleteData){

Node currentNodePtr = headPtr.getNextNodePtr();

Node prevNodePtr = headPtr;

Node nextNodePtr = headPtr;

while (currentNodePtr != null){

if (currentNodePtr.getData() == deleteData){

nextNodePtr = currentNodePtr.getNextNodePtr();

break;

}

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr.getNextNodePtr();

}

prevNodePtr.setNextNodePtr(nextNodePtr);

}

public void IterativePrint(){

Node currentNodePtr = headPtr.getNextNodePtr();

while (currentNodePtr != null){

System.out.print(currentNodePtr.getData()+" ");

currentNodePtr = currentNodePtr.getNextNodePtr();

}

System.out.println();

}

public int countList(){

Node currentNodePtr = headPtr.getNextNodePtr();

int countElements = 0;

while (currentNodePtr != null){

//System.out.print(currentNodePtr.getData()+" ");

countElements++;

currentNodePtr = currentNodePtr.getNextNodePtr();

}

return countElements;

}

}

class Queue{

private int array[];

private int maxSize; // useful to decide if resizing (doubling the array size) is needed

private int endOfQueue; // same as endOfArray

public Queue(int size){

array = new int[size];

maxSize = size;

endOfQueue = -1;

}

public boolean isEmpty(){

if (endOfQueue == -1)

return true;

return false;

}

public void resize(int s){

int tempArray[] = array;

array = new int[s];

for (int index = 0; index

array[index] = tempArray[index];

}

maxSize = s;

}

public void enqueue(int data){ // same as insert 'at the end'

if (endOfQueue == maxSize-1)

resize(2*maxSize);

array[++endOfQueue] = data;

}

public int peek(){

if (endOfQueue >= 0)

return array[0];

else

return -1000000;// an invalid value indicating

// queue is empty

}

public int dequeue(){

if (endOfQueue >= 0){

int returnVal = array[0];

for (int index = 0; index

array[index] = array[index+1];

endOfQueue--;

// the endOfQueue is decreased by one

return returnVal;

}

else

return -1000000; // an invalid value indicating

// queue is empty

}

}

class Graph{

private int numNodes;

private List[] adjacencyList;

private int[] levelNumbers;

private int[] predecessorList;

Graph(int n){

numNodes = n;

adjacencyList = new List[numNodes];

levelNumbers = new int[numNodes];

predecessorList = new int[numNodes];

for (int id = 0; id

adjacencyList[id] = new List();

}

public void addEdge(int u, int v){

adjacencyList[u].insert(v);

adjacencyList[v].insert(u);

}

public List getNeighborList(int id){

return adjacencyList[id];

}

public int getLevelNumber(int id){

return levelNumbers[id];

}

public int getPredecessor(int id){

return predecessorList[id];

}

public void RunBFS(int startNodeID){

boolean[] visitedNodes = new boolean[numNodes];

for (int id = 0; id

levelNumbers[id] = -1;

visitedNodes[id] = false;

predecessorList[id] = -1;

}

levelNumbers[startNodeID] = 0;

visitedNodes[startNodeID] = true;

Queue FIFOQueue = new Queue(1);

FIFOQueue.enqueue(startNodeID);

while (!FIFOQueue.isEmpty()){

int firstNodeID = FIFOQueue.dequeue();

int neighborListSize = adjacencyList[firstNodeID].countList();

for (int index = 0; index

int neighborID = adjacencyList[firstNodeID].read(index);

if (!visitedNodes[neighborID]){

visitedNodes[neighborID] = true;

FIFOQueue.enqueue(neighborID);

levelNumbers[neighborID] = levelNumbers[firstNodeID] + 1;

predecessorList[neighborID] = firstNodeID;

}

}

}

}

}

class Graph_BFS_ShortestPaths_Solution{

public static void main(String[] args){

try{

Scanner input = new Scanner(System.in);

String graphEdgesFilename;

System.out.print("Enter the file name for the edges of the graph: ");

graphEdgesFilename = input.next();

int numNodes;

System.out.print("Enter number of nodes: ");

numNodes = input.nextInt();

Graph graph = new Graph(numNodes);

FileReader fr = new FileReader(graphEdgesFilename);

BufferedReader br = new BufferedReader(fr);

String line = null;

while ( (line = br.readLine() ) != null){

StringTokenizer stk = new StringTokenizer(line);

int uNodeID = Integer.parseInt(stk.nextToken());

int vNodeID = Integer.parseInt(stk.nextToken());

graph.addEdge(uNodeID, vNodeID);

}

graph.RunBFS(0);

// Add code here

}

catch(Exception e){e.printStackTrace();}

}

}

Project 8: Use the Results of Breadth First Search to Extract the Shortest Paths from a Particular Vertex to the Rest of the Vertices in an Undirected Graph Due: April 19, 2018: by 1 PM (in Canvas) The objective of this project is to use the Breadth First Search (BFS) algorithm to determine the shortest paths (and print them) from a particular vertex to the rest of the vertices in the graph. You are given the code for running the BFS algorithm starting from a particular vertex (say, vertex 0). The Graph class has member variables to keep track of the predecessor vertex for every vertex (in the form of the predecessorList array) on the BFS tree rooted at the starting vertex. The code given for the BFS algorithm also updates the entries in the predecessorList array as part of the traversal. Your task in this project would be to use the results (like the entries in the predecessorList array) of running the BFS algorithm starting from vertex 0 and write an iterative or recursive function that would print the actual shortest paths (sequence of edges) from vertex 0 to the rest of the vertices in the graph. You could add the iterative or recursive function as part of the Graph class and access it from the mairn function. Your main function can also print the predecessor for every vertex in the BFS tree rooted at vertex 0, as shown in the sample output. A sample output (printing the predecessor entries and the shortest paths from vertex 0) for an example graph is shown below ter the file nane for the edges of the graph: graphEdges 2.txt nter nunber of nodes: 8 decessor List Entries edecessor of 1 decessor of 1 3 edecessor of 2 1 edecessor of 3 1 edecessor of 42 redecessor of 5 3 redecessor of 6 4 decessor of 7:0 2 4 hortest Patha fron Uertex B 13 - 1-2 46 Submission (as one Word or PDF document) (1) The entire code, including the function added to the Graph class to print the shortest paths from the starting vertex (0) to the rest of the vertices in the graph. (2) Do this manually: Draw a graph of 10 or more vertices, run the BFS algorithm on the graph (and identify the tree edges that connect a vertex to its predecessor vertex) and list down the predecessor for each vertex in the graph. The predecessor for the root vertex (0) is set as-1 and every other vertex should have a valid entry for its predecessor vertex in the BFS tree rooted at vertex 0. Using the tree edges, also list the shortest paths from vertex 0 to every other vertex in the graph (as shown in the sample screenshot above) (3) Construct the edge list file for the test graph of 10 or more vertices created in part-2 and input the edge list file and the number of vertices to the code developed in part-1 and generate the output (for the list and the shortest paths from vertex 0) similar to the one shown in screenshot. The outputs in part-2 and part-3 are expected to match, if ties (arising while deciding to visit a neighbor vertex) are broken in favor of vertices with lower ID. Project 8: Use the Results of Breadth First Search to Extract the Shortest Paths from a Particular Vertex to the Rest of the Vertices in an Undirected Graph Due: April 19, 2018: by 1 PM (in Canvas) The objective of this project is to use the Breadth First Search (BFS) algorithm to determine the shortest paths (and print them) from a particular vertex to the rest of the vertices in the graph. You are given the code for running the BFS algorithm starting from a particular vertex (say, vertex 0). The Graph class has member variables to keep track of the predecessor vertex for every vertex (in the form of the predecessorList array) on the BFS tree rooted at the starting vertex. The code given for the BFS algorithm also updates the entries in the predecessorList array as part of the traversal. Your task in this project would be to use the results (like the entries in the predecessorList array) of running the BFS algorithm starting from vertex 0 and write an iterative or recursive function that would print the actual shortest paths (sequence of edges) from vertex 0 to the rest of the vertices in the graph. You could add the iterative or recursive function as part of the Graph class and access it from the mairn function. Your main function can also print the predecessor for every vertex in the BFS tree rooted at vertex 0, as shown in the sample output. A sample output (printing the predecessor entries and the shortest paths from vertex 0) for an example graph is shown below ter the file nane for the edges of the graph: graphEdges 2.txt nter nunber of nodes: 8 decessor List Entries edecessor of 1 decessor of 1 3 edecessor of 2 1 edecessor of 3 1 edecessor of 42 redecessor of 5 3 redecessor of 6 4 decessor of 7:0 2 4 hortest Patha fron Uertex B 13 - 1-2 46 Submission (as one Word or PDF document) (1) The entire code, including the function added to the Graph class to print the shortest paths from the starting vertex (0) to the rest of the vertices in the graph. (2) Do this manually: Draw a graph of 10 or more vertices, run the BFS algorithm on the graph (and identify the tree edges that connect a vertex to its predecessor vertex) and list down the predecessor for each vertex in the graph. The predecessor for the root vertex (0) is set as-1 and every other vertex should have a valid entry for its predecessor vertex in the BFS tree rooted at vertex 0. Using the tree edges, also list the shortest paths from vertex 0 to every other vertex in the graph (as shown in the sample screenshot above) (3) Construct the edge list file for the test graph of 10 or more vertices created in part-2 and input the edge list file and the number of vertices to the code developed in part-1 and generate the output (for the list and the shortest paths from vertex 0) similar to the one shown in screenshot. The outputs in part-2 and part-3 are expected to match, if ties (arising while deciding to visit a neighbor vertex) are broken in favor of vertices with lower ID