use matlab code and upload the screenshot thanks

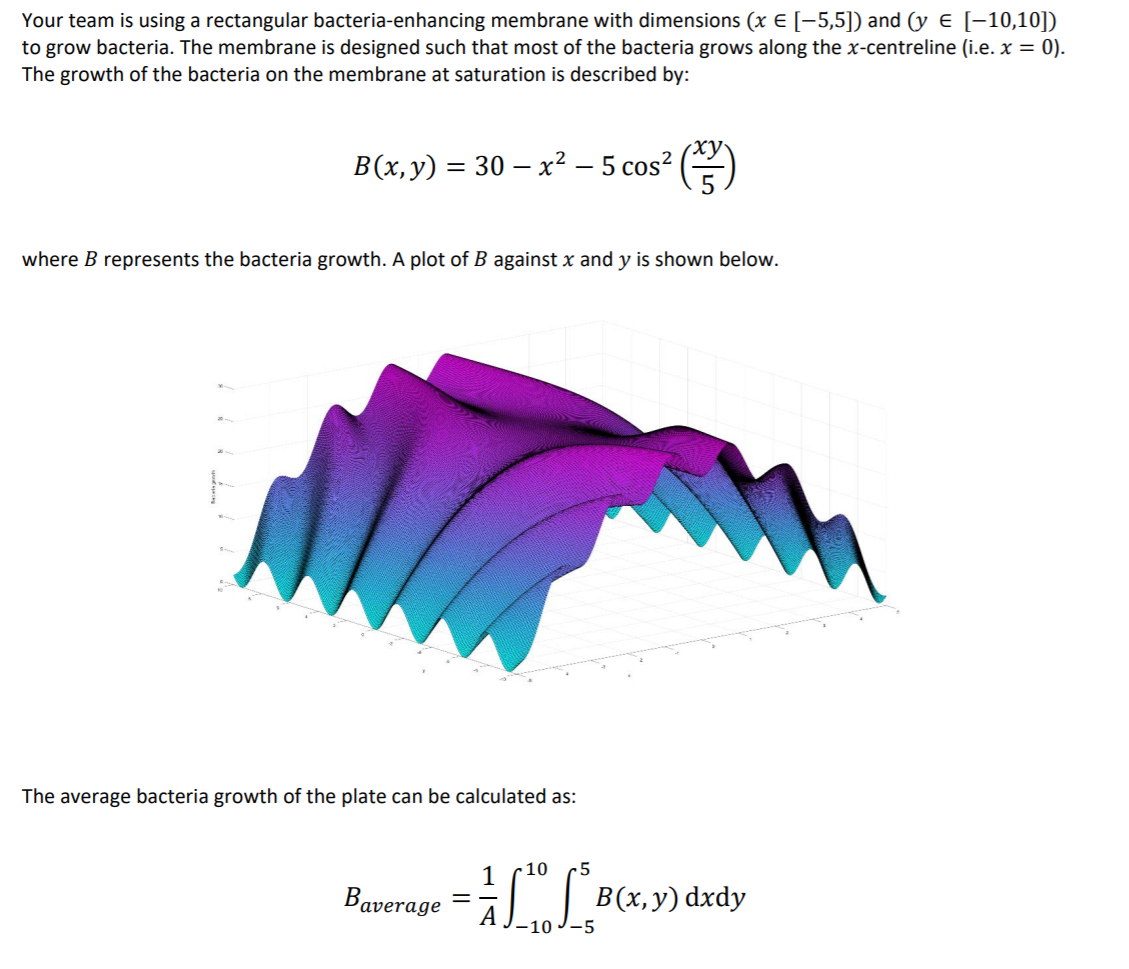
Your team is using a rectangular bacteria-enhancing membrane with dimensions (x (-5,5]) and (y E (-10,10]) to grow bacteria. The membrane is designed such that most of the bacteria grows along the x-centreline (i.e. x = 0). The growth of the bacteria on the membrane at saturation is described by: B(x,y) = 30 x2 5 cos? (2) where B represents the bacteria growth. A plot of B against x and y is shown below. The average bacteria growth of the plate can be calculated as: 1 - 10 5 Baverage B(x, y) dxdy -10 The composite Simpson's 3/8 rule is given by kom =3(E)- Ermo)+(ro) +rs In the comp simp38 vector.m file, complete the function file for the Composite Simpson's 3/8 rule which integrates the vector inputs. The function should print an error statement if an incorrect number of points is supplied for integration. *You should have six figure windows by the end of this task. Q2b In the Q2b.m file, calculate the average bacteria on the membrane using the composite Simpson's 3/8 rule using 127 equally-spaced points in each direction (x and y). Start by evaluating the inner integral along the x dimension for each value of y. The resulting values can then be integrated along the y dimension for the outer integral. The membrane is designed to curate an average bacteria growth greater than 20. Does this membrane achieve the required amount or does the membrane need to be redesigned? Use fprintf() to print a statement containing the average bacteria growth to 2 decimal places and whether the membrane needs to be redesigned. *You should have six figure windows by the end of this task. Your team is using a rectangular bacteria-enhancing membrane with dimensions (x (-5,5]) and (y E (-10,10]) to grow bacteria. The membrane is designed such that most of the bacteria grows along the x-centreline (i.e. x = 0). The growth of the bacteria on the membrane at saturation is described by: B(x,y) = 30 x2 5 cos? (2) where B represents the bacteria growth. A plot of B against x and y is shown below. The average bacteria growth of the plate can be calculated as: 1 - 10 5 Baverage B(x, y) dxdy -10 The composite Simpson's 3/8 rule is given by kom =3(E)- Ermo)+(ro) +rs In the comp simp38 vector.m file, complete the function file for the Composite Simpson's 3/8 rule which integrates the vector inputs. The function should print an error statement if an incorrect number of points is supplied for integration. *You should have six figure windows by the end of this task. Q2b In the Q2b.m file, calculate the average bacteria on the membrane using the composite Simpson's 3/8 rule using 127 equally-spaced points in each direction (x and y). Start by evaluating the inner integral along the x dimension for each value of y. The resulting values can then be integrated along the y dimension for the outer integral. The membrane is designed to curate an average bacteria growth greater than 20. Does this membrane achieve the required amount or does the membrane need to be redesigned? Use fprintf() to print a statement containing the average bacteria growth to 2 decimal places and whether the membrane needs to be redesigned. *You should have six figure windows by the end of this task