Question
Use R A roulette wheel has 18 red pockets, 18 black pockets and 2 green ones. So, playing a color in one game of roulette
Use R
A roulette wheel has 18 red pockets, 18 black pockets and 2 green ones. So, playing a color in one game of roulette is equivalent to drawing from the urn. Suppose a very small casino hires you to consult on whether they should set up roulette wheels. To keep the example simple, we will assume that 1,000 people will play and that the only game you can play on the roulette wheel is to bet on red or black. The casino wants you to predict how much money they will make or lose. They want a range of values and, in particular, they want to know what's the chance of losing money. If this probability is too high, they will pass on installing roulette wheels. In this case, you are required to use two ways to answer the question: The first way is to use simulation to approximate the probability and the second way is to use central limit theorem (CLT) to get the theorical probability.
Hints:
# If red comes up, the gambler wins and the casino loses a dollar, so we draw a -$1.
# Otherwise, the casino wins a dollar and we draw a $1.
# Let X be one draw and S be the sum of drawing, S=sum(X)
Step1: Use the function rep to generate the urn of "-1" and "1" based on the proportion or numbers for one experiment to get X. For example,
X
Step2: Get the sum of X because we want to know if the casino will win or not. It means S=sum(X) should be less than 0.
Step 3: Conduct 10,000 Monte Carlosimulations of the previous experiment with function replicate to get the distribution of S. For example
B
events
Step 4: How often (what probability) did we get sums less than 0 from the simulations?
Step 5: Plot the distribution of S for 10,000 times experiments
Step 6: Get the mean value and standard deviation based on the simulation for X and S using mean() and sd() functions
Step 7: Get the expected value and standard error (or we can say it as "standard deviation) of the sum of the draws(S) based on the formulas below.
In general, if the urn has two possible outcomes, say a ("1" in our case)andb ("-1" in our case) for variable X, with proportions p and 1p respectively, the expected value and standard deviation of X are:
Expected value [average of the numbers in the urn]: E(X)=ap + b(1-p)
Standard deviation [standard deviation of the numbers in the urn]:
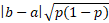
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


