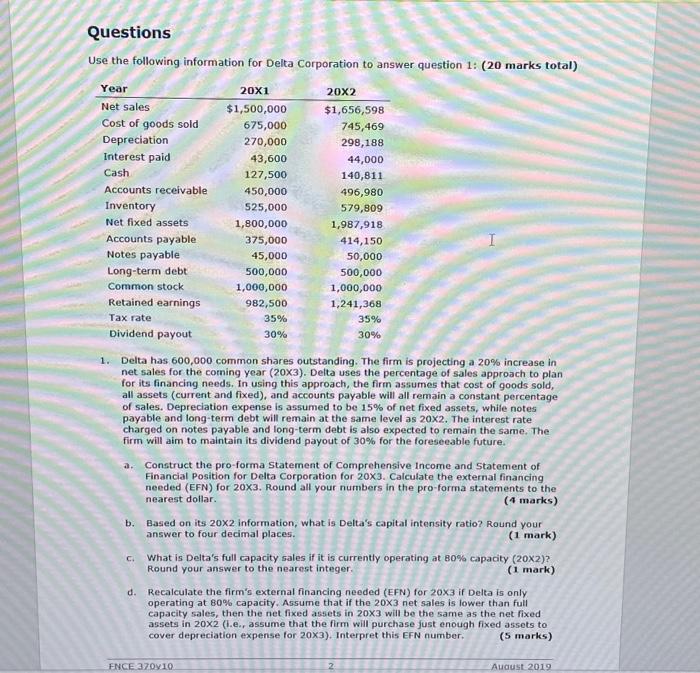
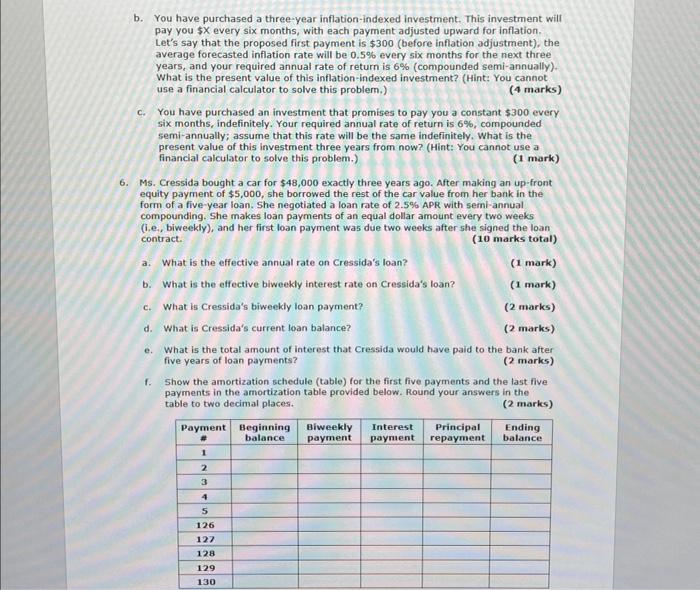
Use the following information for Delta Corporation to answer question 1: (20 marks total) 1. Delta has 600,000 common shares outstanding. The firm is projecting a 20% increase in net sales for the coming year (20x3). Delta uses the percentage of sales approach to plan for its financing needs. In using this approach, the firm assumes that cost of goods sold, all assets (current and fixed), and accounts payable will all remain a constant percentage of sales. Depreciation expense is assumed to be 15% of net fixed assets, while notes payable and long-term debt will remain at the same level as 202. The interest rate charged on notes payable and long-term debt is also expected to remain the same. The firm will aim to maintain its dividend payout of 30% for the foreseeable future. a. Construct the pro-forma Statement of Comprehensive Income and Statement of Financial Position for Delta Corporation for 203. Calculate the external financing needed (EFN) for 20X3. Round all your numbers in the pro-forma statements to the nearest dollar. (4 marks) b. Based on its 202 information, what is Delta's capital intensity ratio? Round your answer to four decimal places. (1 mark) c. What is Delta's full capacity sales if it is currently operating at 80% capacity (20X2)? Round your answer to the nearest integer. (1 mark) d. Recalculate the firm's external financing needed (EFN) for 203 if Delta is only operating at 80% capacity. Assume that if the 203 net sales is lower than full capacity sales, then the net fixed assets in 203 will be the same as the net fixed assets in 202 (i.e., assume that the firm will purchase just enough fixed assets to cover depreciation expense for 203 ). Interpret this EFN number. (5 marks) e. What is Delta's internal growth rate for 202 ? Round your final answer in percentage to two decimal places. (2 marks) f. What is Delta's sustainable growth rate for 202 ? Round your final answer in percentage to two decimal places. (2 marks) 9. Assume that Delta is operating at 100% capacity. Calculate the EFN for the firm if it wants to grow its sales by 100% for 203. Interpret this EFN number. (S marks) 2. A firm's sustainable growth rate can be calculated using the formula Sustainable growth rate =(P(S/A)(1+D/E)R)/[1(P(S/A)(1+D/E)R)] Discuss the relationship between sustainable growth rate and each of the four variables in the above formula. (4 marks) 3. Use the present value and future value formulas to solve the following problems. Confirm your answers with your financial calculator. Show both methods of calculation in your answers. When performing your calculations, keep as many decimal places as you can for intermediate answers, but round your final answers to two decimal places. (10 marks totaI) 3. If you invest $1000 today at 3% annual interest rate, how much money would you have in i) one year's time? (1 mark) ii) 10 years' time? (1 mark) iii) 30 years' time? (1 mark) b. You estimate that you will need $350,000 to buy a house some time in the future. If your bank account pays an annual interest rate of 3%, how much money must you deposit now to purchase the house in i) one year's time? (1 mark) ii) 10 years'time? (1 mark) iii) 30 years' time? (1 mark) c. You are saving up to buy a $10,000 used car. You currently have $5,000 in your savings account, which pays an interest rate of 3%. If you do not put any more money into this savings account, how long will you have to wait before you can buy the used car? (2 marks) d. You are saving up to buy a $10,000 used car. You currently have $,000 in your savings account. If you do not put any more money into this savings account, what interest rate (in percentage) must you eam to achieve your goal of buying the used car in two years' time? (2 marks) 4. This question consists of four main parts. When performing the calculations, keep as many decimal places as you can for intermediate answers, but round your final answers to two decimal places. (13 marks total) a. If you save $200 per month for 10 years at 12% annual percentage rate with monthly compounding. i) what is the future value annuity factor? ii) what is the future value? (1 mark) (1 mark) b. Suppose that you have a choice between receiving $10,000 now and receiving $1000 per month for the next 12 months. Assuming that you can Ipvest at a 12% annual percentage rate (APR) with monthly compounding, what is i) the present value annuity factor? ii) the present value? iii) your choice? (1 mark) (1 mark) (1 mark) iv) the break-even annual rate of return at which you are indifferent between receiving $10,000 now and receiving $1000 per month for 12 months? (2 marks) v) the break-even number of monthly payments at which you are indifferent between receiving $10,000 now and receiving $1000 per month, given an APR of 12% with monthly compounding? (1 mark) vi) the break-even dollar amount of monthly payments, given an APR of 12% with inonthly compounding and 12 months of payments? (1 mark) (Hint: Use the financial calculator for parts (iv), (v), and (vi), Clearly show the inputs you use for each calculation.) c. You are saving $200 per month at 6% annual percentage return (APR) with monthly compounding. How many years will it take for your savings to accumulate to $10,000 ? (Hint: Use the financial calculator for this calculation, and clearly show the inputs you use.) (2 marks) d. You are saving $200 per month. What annual percentage rate of retum must be earned for your savings to accumulate to $30,000 in 10 years? (2 marks) 5. This question consists of three parts. When performing the calculations, keep as many decimal places as you can for intermediate answers, but round your final answers to two decimal places. (7 marks total) a. You have taken out a loan that requires you to repay $200 per month for 10 years. at 12% annual percentage rate with monthly compounding. The first payment occurs today. What is the current value of this loan? (2 marks) b. You have purchased a three-year inflation-indexed investment. This investment will pay you $ every six months, with each payment adjusted upward for inflation. Let's say that the proposed first payment is $300 (before inflation adjustment), the average forecasted inflation rate will be 0.5% every six months for the next three years, and your required annual rate of retum is 6% (compounded semi-annually). What is the present value of this inflation-indexed investment? (Hint: You cannot use a financial calculator to solve this problem.) (4 marks) c. You have purchased an investment that promises to pay you a constant $300 every six months, indefinitely. Your required annual rate of return is 6%, compounded semi-annually; assume that this rate will be the same indefinitely. What is the present value of this investment three years from now? (Hint: You cannot use a financial calculator to solve this problem.) (1 mark) 6. Ms. Cressida bought a car for $48,000 exactly three years ago. After making an up-front equity payment of $5,000, she borrowed the rest of the car value from her bank in the form of a five-year loan. She negotiated a loan rate of 2.5% APR with semi-annual compounding. She makes loan payments of an equal dollar amount every two weeks (i.e, biweekly), and her first loan payment was due two weeks after she signed the loan contract. (10 marks total) a. What is the effective annual rate on Cressida's loan? b. What is the effective biweekly interest rate on Cressida's loan? c. What is Cressida's biweekly loan payment? d. What is Cressida's current loan balance? (1 mark) (1 mark) (2 marks) (2 marks) e. What is the total amount of interest that Cressida would have paid to the bank after five years of loan payments? ( 2 marks) f. Show the amortization schedule (table) for the first five payments and the last five payments in the amortization table provided below. Round your answers in the table to two decimal places. (2 marks) 7. You are making plans for your retirement. You have just turned 30 and want to retire on your 65th birthday. Once retired, you plan to move to a tax-free Caribbean state, where you believe you can live comfortably on your retirement savings. You plan to make your first withdrawal from your retirement savings when you retire at age 65 and your last withdrawal one month before your 85th birthday. Based on family history, you expect to live until exactly age 85 . Your plan is to have a total of $1 million when you retire. Your current salary is $36,000 per year, or $3,000 per month. Your personal tax rate is approximately 30%. You estimate that you can earn an average return of 12% APR compounded annually on any money you invest over the next 60 years. You want to start putting aside a fixed amount of money at the end of every month until your retirement at age 65 . You will make your first deposit one month from now and your last deposit on your 65th birthday. a. To ensure that you are able to achieve your retirement objective, what is the maximum percentage of your after-tax monthly income that you can spend? (4 marks) b. Given that you have $1 million in your retirement savings at age 65 , what is the fixed monthly dollar amount that you can withdraw until age 85? Assume no taxes will be levied when you withdraw your retirement savings. (3 marks) 8. You have just received an inheritance of $20,000. You wish to invest in fixed income securities such as bonds, which you think are less risky than stocks. After some research, you have narrowed down your choices to the following three fixed income securities: One-year Treasury Bill: Face value of $1000 Yield to maturity of 1.74% Coupon Bond A: Two years to maturity Face value of $1000 Coupon rate of 3%, with semi-annual coupon payments Price multiple of face value =1.0189 Coupon Bond B: Five years to maturity Face value of $1000 Coupon rate of 3.5%, with annual coupon payments Yield to maturity of 2.51% All yields to maturity are compounded semi-annually. a. What is the price of the one-year treasury bill? b. What is the yield to maturity on Coupon Bond A? (9 marks total) (2 marks) (2 marks) c. What is the price of Coupon Bond B? (2 marks) d. If the inflation rate is 1.5%, what are the real yields on the one-year treasury bill, Coupon Bond A, and Coupon Bond B ? (2 marks) e. If your personal real hurdle rate (the minimum rate of return required on investments) is 1%, which of the three fixed income securities would you choose to invest in? (1 mark) Answer the following questions on bond valuation and duration. (9 marks total) a. Calculate the duration of a zero-coupon bond with five years to maturity, face value of $1000, and effective annual yield of 12.1604%. Show your calculations. What does your answer say about the duration of zero-coupon bonds in general? (2 marks) b. Calculate the duration of a coupon bond with the following features. What general conclusion can we make about the duration of coupon bonds relative to their time to maturity? (3 marks) Face value of $1000 Five years to maturity Coupon rate of 11%, paid semi-annually Current price of $970 (Hint: The effective annual yield should be 12.1604%.) c. Duration is a measure of interest rate risk. Specifically, it measures the approximate percentage change in bond price given a small percentage change in interest rate ( % bond price change / % interest rate change). For example, for a bond with a duration of five years, a 0.1% change in interest rate would change the bond's price by 50.1%=0.5%, approximately. Suppose that the interest rates on all bonds increase uniformly by 0.1% (this is what is commonly called a "parallel upward shift in yields of 10 basis points"). What is the percentage change in the price on the coupon bond in part (b)? What is the approximate coupon bond price? Note that bond yield and bond price are inversely related to each other (i.e., an increase in yield should lead to a decrease in bond price). (2 marks) d. Recalculate the price of the coupon bond with five years to maturity, face value of $1000, coupon rate of 11% paid semi-annually, and a new yield to maturity equaling the original yield in part (b) plus 0.1%. Does it concur with your approximate coupon bond price calculated in part (c) ? (Hint: The two answers in parts (c) and (d) should be fairly similar.) (2 marks) 10. Aunt Kathleen owns 3000 preferred shares of ABC Inc., and she is thinking of selling 100 of these shares to pay for a new computer. These shares pay a stable quarterly dividend of $0.65 per share (i.e., there will be four dividend payments in a year, and each payment is $0.65 per share). Aunt Kathleen's required retum is 12% APR compounded semi-annually. a. What is the effective annual return (EAR) based on an APR of 12% compounded semi-annually? (1 mark) b. What is the effective return per dividend payment period for Aunt Kathleen? (1 mark) c. What is the estimated stock price based on the Constant Dividend model? (2 marks) d. What is the maximum amount of money that Aunt Kathleen can spend on the new computer if she only uses the receipts from the sale of 100 shares of ABC's preferred shares to pay for it? (1 mark) 11. GeoTech Company will be holding an IPO of two million shares tomorrow. Market expectations are high for this IPO. The company is expected to pay $1.00 per share starting one year from now. The dividends are then expected to grow at a supernormal rate of 25% for three years, before dropping down to 15% for three more years, and then to 7% afterwards. The 7% growth is then expected to continue for the foreseeable future. What is the gross dollar amount that will be raised from this ipo if the required return for similar issues is 16% ? Hint: The first dividend is $1.00. (6 marks)