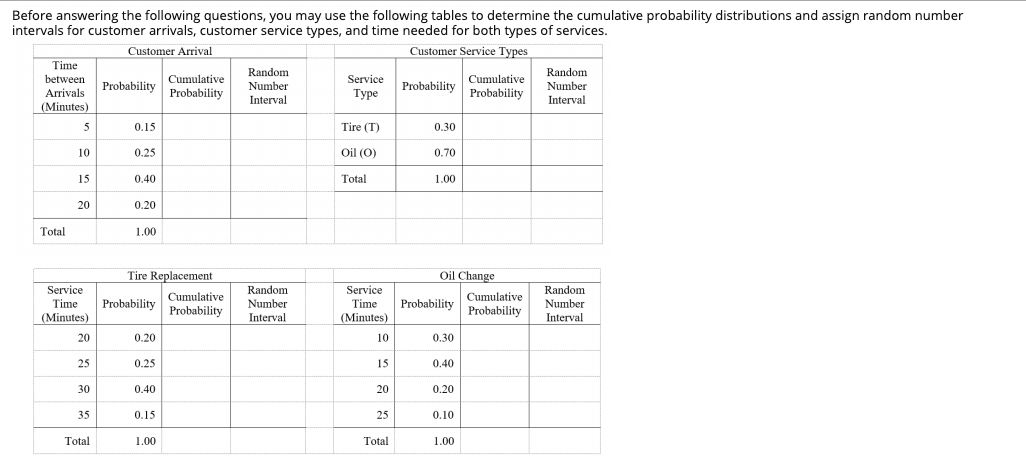
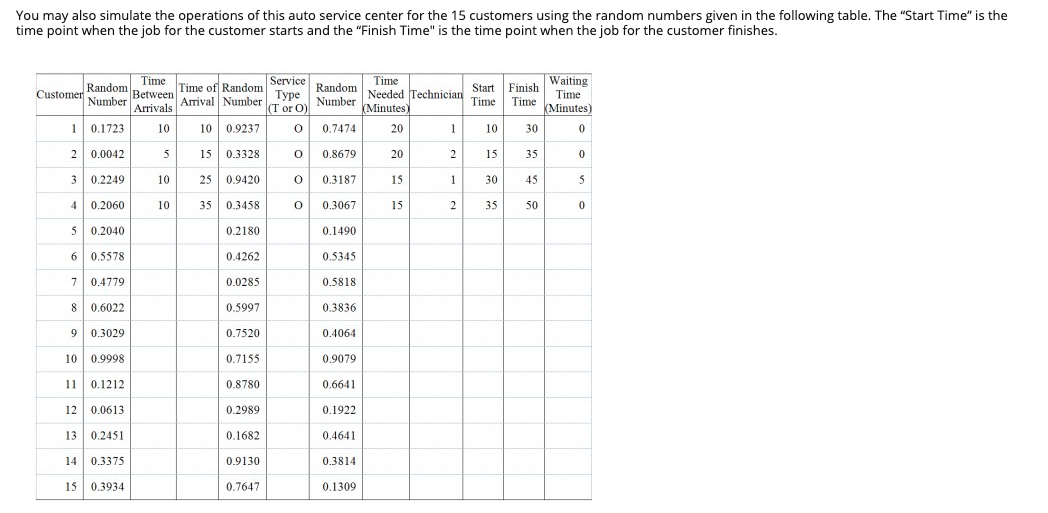
Use the following scenario and data for all questions An auto service center provides two types of services, Tire Replacement (T) and Oil Change (O). About 30% of the customers are for Tire Replacement and the other 70% are for Oil Change. All customers are serviced on a first come first served basis. During regular hours, customers arrive at the service center according to the probability distribution in the following table Time Between Arrivals (Minutes)ca Probabilitya 0.15 10 0.25a 15c 0.40a irs 0.20a 20 Totala 1.00a Two technicians are working at the service center and both of them are skillful enough for both Tire Replacement and Oil Change. Once finishing the job for a customer, a technician will take care of the next customer waiting in line. When both technicians are idle, the one who finished the last job earlier will take care of the next incoming customer. The times taken by the two jobs by any of the technicians follow the probability distributions in the following tables. You are required to simulate the operations of the auto service center for 15 customers. Tire Replacement Service Time (Minutes) Probability Oil Change Service Time (Minutes) Probability 20 0.20 10 0.30 25 0.25 15 0.40 30 0.40 20 0.20 35 0.15 25 0.10 Total 1.00 Total 1.00 Before answering the following questions, you may use the following tables to determine the cumulative probability distributions and assign random number intervals for customer arrivals, customer service types, and time needed for both types of services. Customer Service Types Customer Arrival Time Random Random between Cumulative Service Cumulative Probability Probability Number Number Arrivals Probability Probability Interval Interval (Minutes) Tire (T) 5 0.15 0.30 10 0.25 Oil (O) 0.70 Total 15 0.40 1.00 20 0.20 Total 1.00 Tire Replacement Oil Change Random Service Service Time Random Cumulative Probability Cumulative Probability Probability Time Number Number Probability (Minutes) Interval (Minutes) Interval 20 0.20 10 0.30 25 0.25 15 0.40 30 0.40 20 0.20 35 0.15 25 0.10 Total 1.00 Total 100 You may also simulate the operations of this auto service center for the 15 customers using the random numbers given in the following table. The "Start Time" is the time point when the job for the customer starts and the "Finish Time" is the time point when the job for the customer finishes. Waiting Time of Random Service Time Time Needed Technician (Minutes) Random Number Random Start Finish Customer Between Arrivals Time Arrival Number Number Time Time (Minutes) (T or O) 0.1723 0.9237 20 10 10 O 0.7474 1 10 30 0 2 0.0042 5 15 0.3328 O 0.8679 20 2 15 35 0 3 0.2249 10 25 0.9420 O 0.3187 15 1 30 45 5 4 0.2060 10 35 0.3458 O 0.3067 15 2 35 50 0 5 0.2040 0.1490 0.2180 6 0.5578 0.5345 0.4262 7 0.4779 0.0285 0.5818 8 0.6022 0.5997 0.3836 9 0.3029 0.7520 0.4064 10 0.9998 0.7155 0.9079 0.8780 11 0.1212 0.6641 12 0.1922 0.0613 0.2989 13 0.2451 0.1682 0.464 14 0.3375 0.9130 0.3814 15 0.3934 0.7647 0.1309 QUESTION 5 For the Tire Replacement, the random number interval assigned to Service Time 25 minutes is 0.0000-0.1999 0.2000-0.4499 0,4500-0.8499 0.8500-0.9999 None of the above QUESTION 6 For the Tire Replacement, the random number interval assigned to Service Time 35 minutes is 0.0000-0.1999 0.2000-0.4499 0,4500-0.8499 0.8500-0.9999 None of the above