1. Using a table similar to that shown in Figure 3.10, calculate 57₁₀ divided by 13₁₀ using the hardware described in Figure 3.8. You should show the contents of each register on each step. Assume both inputs are unsigned 6-bit integers.

1. (1 pt) Whats the binary value of 57₁₀? Express as a 6-bit unsigned integer

______ ______

Place this value into the right 6 bits of the remainder field in the table below.

2. (1 pt) What about 13₁₀? Express as a 6-bit unsigned integer. ______ ______

Place the 6 bits into the high (first) 6 bits of the Divisor field.

3. (1 pt) When you add six 0s to the right end of the divisor, you are shifting it left 6 positions, or multiplying it by 2^6. Whats the new number in decimal? _______

A side note: that divisor you just calculated is what youre actually going to start off subtracting from the remainder. Then after each step, youll divide the divisor by 2, discarding any fractional part, subtracting it from the remainder again. As you can see, youre going to have to divide the divisor in half a bunch of times before its small enough to be subtracted from remainder with a result 0. Thats how many steps you have to progress before you start inserting 1s into the quotient.

4. (13 pts, 1 per step group) Complete the table below. Ive provided what we all know is the answer at the end. Your job is to get there too. For division, stop after n+1 steps = 7.

		Divisor in Dec	Remainder in Dec
		13	57
Step	Action	Quotient	Divisor	Remainder
0	Load values	_____ _____	_____ _____ _____ _____	_____ _____ _____ _____
1.1	Remainder = Rem Div			_____ _____ _____ _____
1.2	Rem	_____ _____		_____ _____ _____ _____
	Rem0, sll Q, Q0=1
1.3	Shift Div right		_____ _____ _____ _____
2.1	Remainder = Rem Div			_____ _____ _____ _____
2.2	Rem	_____ _____		_____ _____ _____ _____
	Rem0, sll Q, Q0=1
2.3	Shift Div right		_____ _____ _____ _____
3.1	Remainder = Rem Div			_____ _____ _____ _____
3.2	Rem	_____ _____		_____ _____ _____ _____
	Rem0, sll Q, Q0=1
3.3	Shift Div right		_____ _____ _____ _____
4.1	Remainder = Rem Div			_____ _____ _____ _____
4.2	Rem	_____ _____		_____ _____ _____ _____
	Rem0, sll Q, Q0=1
4.3	Shift Div right		_____ _____ _____ _____
5.1	Remainder = Rem Div			_____ _____ _____ _____
5.2	Rem	_____ _____		_____ _____ _____ _____
	Rem0, sll Q, Q0=1
5.3	Shift Div right		_____ _____ _____ _____
6.1	Remainder = Rem Div			_____ _____ _____ _____
6.2	Rem	_____ _____		_____ _____ _____ _____
	Rem0, sll Q, Q0=1
6.3	Shift Div right		_____ _____ _____ _____
7.1	Remainder = Rem Div			_____ _____ _____ _____
7.2	Rem	_____ _____		_____ _____ _____ _____
	Rem0, sll Q, Q0=1
7.3	Shift Div right		_____ _____ _____ ____
	FINAL ANSWER	Quotient: 4	13x4+5=57	Remainder: 5

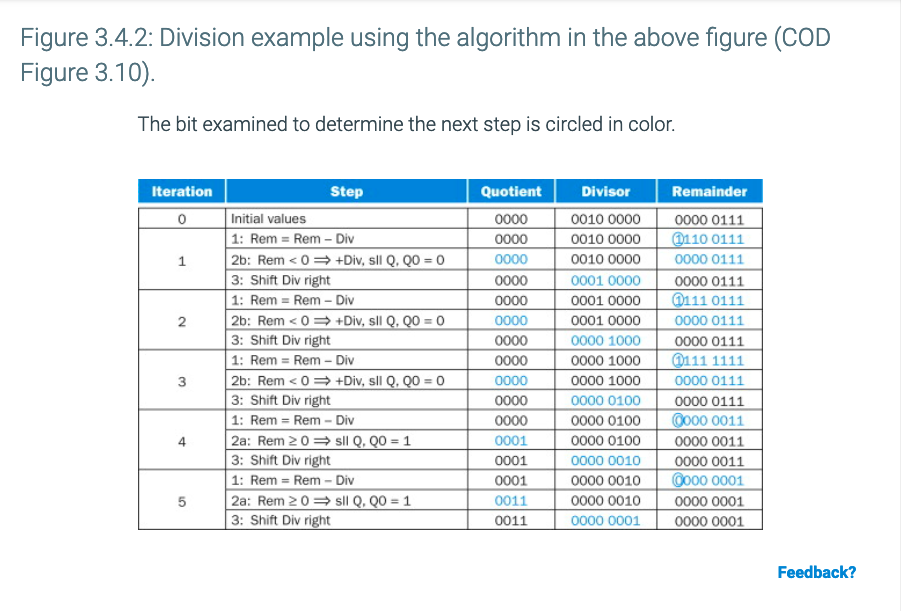
Figure 3.4.2: Division example using the algorithm in the above figure (COD Figure 3.10) The bit examined to determine the next step is circled in color Iteration Step Quotient Divisor Remainder 0 Initial values 1: Rem= Rem-Div 0010 0000 0010 0000 0010 0000 0001 0000 000 0111 0001 0000 0001 0000 0000 1000 0000 0111 0000 1000 0000 1000 0000 0111 0000 0100 0000 0111 0000 0100 0000 01000000 0011 0000 0010 0000 0011 0000 001O 0 0001 0000 0111 10 0111 0000 0111 3: Shift Div right 1: Rem RemDiv 2b: Rem