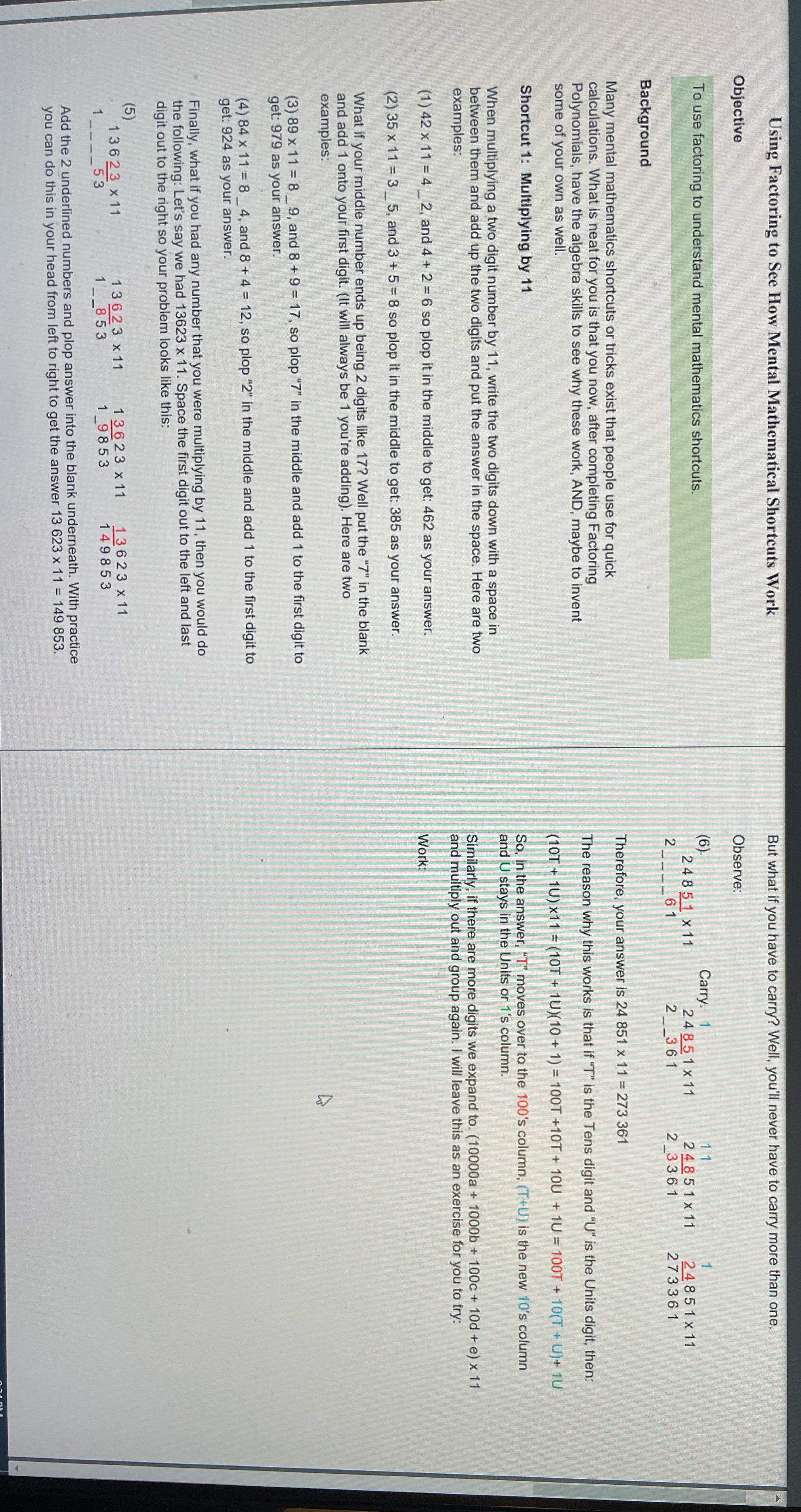
Using Factoring to See How Mental Mathematical Shortcuts Work Objective To use factoring to understand mental mathematics shortcuts. Background Many mental mathematics shortcuts or tricks exist that people use for quick calculations. What is neat for you is that you now, after completing Factoring Polynomials, have the algebra skills to see why these work, AND, maybe to invent some of your own as well. Shortcut 1: Multiplying by 11 When multiplying a two digit number by 11, write the two digits down with a space in between them and add up the two digits and put the answer in the space. Here are two examples: (1)42x11=4_2 and 4 + 2 = 6 so plop it in the middle to get: 462 as your answer. (2)35x11=3_5,and 3 + 5= 8 so plop it in the middle to get: 385 as your answer. What if your middle number ends up being 2 digits like 17? Well put the \"7" in the blank and add 1 onto your first digit. (It will always be 1 you're adding). Here are two examples: (3)89x11=8_9,and 8 +9 = 17, so plop \"7" in the middle and add 1 to the first digit to get: 979 as your answer. (4)84x11=8_4,and 8 +4 = 12, so plop *2" in the middle and add 1 to the first digit to get: 924 as your answer. Finally, what if you had any number that you were multiplying by 11, then you would do the following: Let's say we had 13623 x 11. Space the first digit out to the left and last digit out to the right so your problem looks like this: @ 13623 x11 13623 x11 136 13623 x 11 1 53 1 53 198 149853 623 x11 1 53 Add the 2 underlined numbers and plop answer into the blank underneath. With practice you can do this in your head from left to right to get the answer 13 623 x 11 = 149 853. But what if you have to carry? Well, you'll never have to carry more than one. Observe: (6) Carry. 1 i 1 24851 x11 24851x11 24851 x11 24851%11 2 61 2 61 20193 61 273361 Therefore, your answer is 24 851 x 11 = 273 361 The reason why this works is that if \"T" is the Tens digit and \"U" is the Units digit, then: (10T + 1U) x11 = (10T + 1U)(10 + 1) = 100T +10T + 10U + 1U = 100T + 10(T + U)+ 1U So, in the answer, \"T" moves over to the 100's column, (T and U stays in the Units or 1's column. is the new 10's column Similarly, if there are more digits we expand to. (10000a + 1000b + 100c + 10d + e) x 11 and multiply out and group again. | will leave this as an exercise for you to try: Work