Using Matlab, solve the system given in the first picture in the bottom using three iterations of the Jacobi method. Begin with an initial guess of each force equal 100, i.e. let each element in the vector of unknowns initially equal 100, x0 = [100; 100; 100; 100; 100; 100] (no submission required).

(a1) What is the final guess of the forces and reactions?

(b1) How does this compare to the solution obtained in the other picture provided?

** Then repeat Problem using three iterations of the Gauss-Seidel method. Use the same initial guess (no submission required).

(a2) What is the final guess of the forces and reactions?

(b2) How does this compare to the solutions obtained in in (a1) and the second picture provided?

((((PLEASE CLEARIFY THE ANSWERS SO I CAN WHICH ONES ARE FOR (a1) & (b1) ON TOP. AND (a2) & (b2) IN THE BOTTOM))))

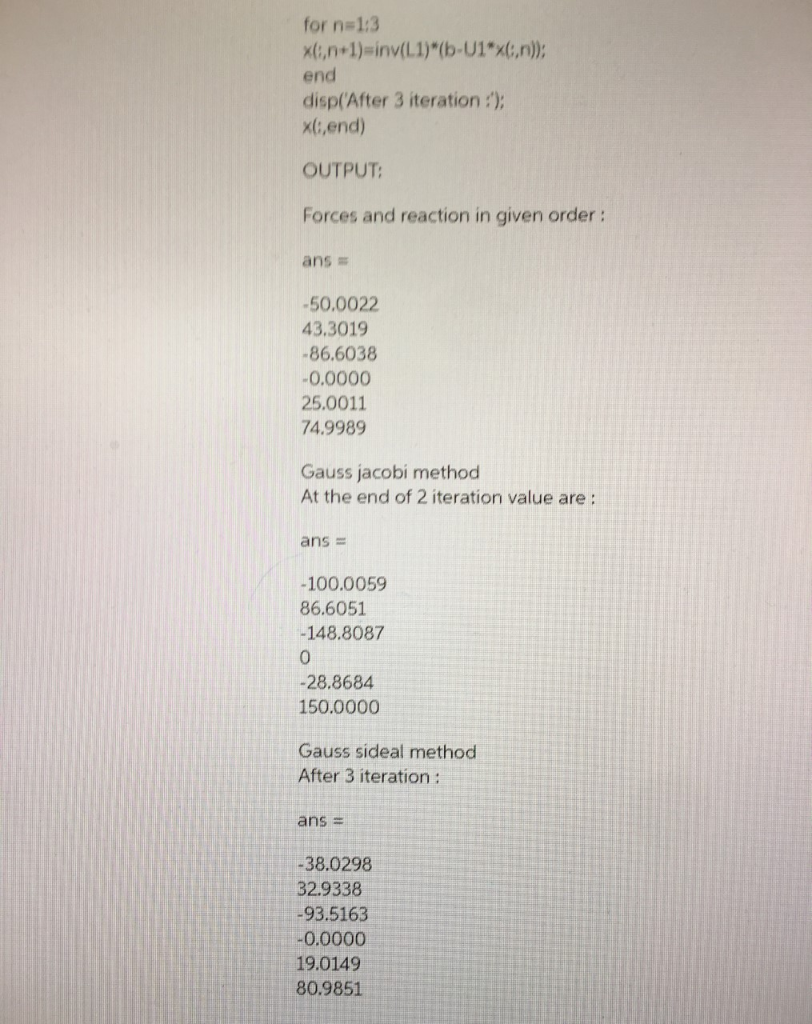
0.866 0.5 001[F 0 100.5 00F 0.5 0.866 0 Fs 0.866 -1.0 0-1.00 0.5 01.oV 0 -1000 3 0 -0.866 0 0-1.0][ts] for n 1:3 end disp(After 3 iteration xc,end) OUTPUT Forces and reaction in given order: ans -50.0022 43.3019 86.6038 0.0000 25.0011 74.9989 Gauss jacobi method At the end of 2 iteration value are: ans -100.0059 86.6051 148.8087 0 -28.8684 150.0000 Gauss sideal method After 3 iteration: ans - -38.0298 32.9338 -93.5163 0.0000 19.0149 80.9851