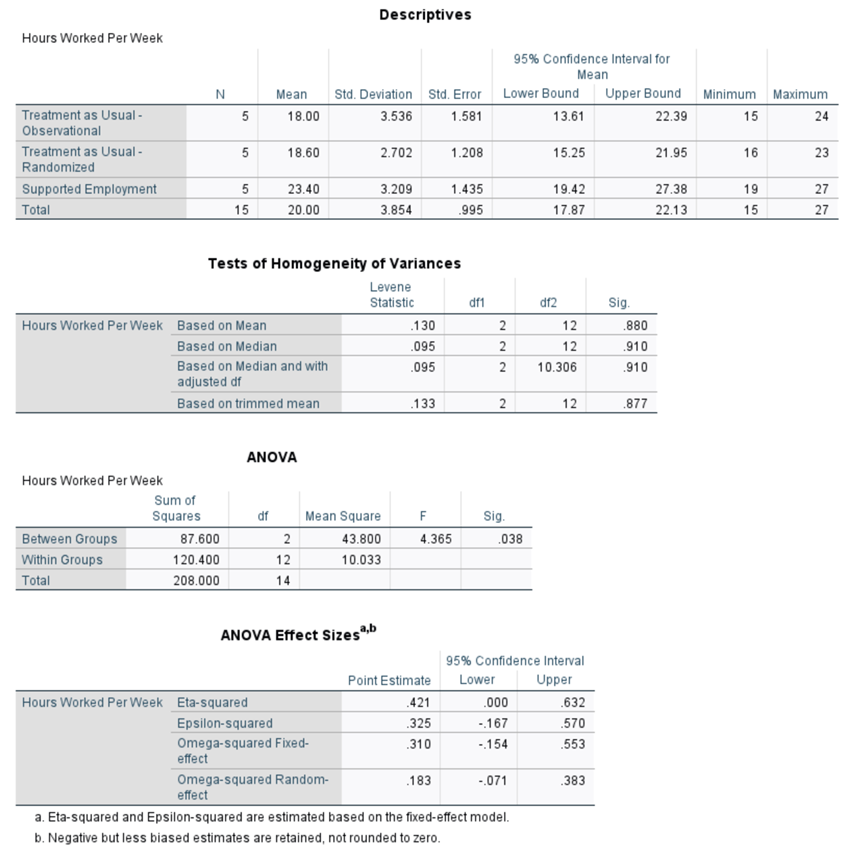
Using the example from Ottomanelli and colleagues (2012), participants were randomized to receive Supported Employment or treatment as usual. A third group, also a treatment as usual group, consisted of a non-randomized observational group of participants. A simulated subset was selected for this example so that the computations would be small and manageable. The independent variable in this example is treatment group (Supported Employment, Treatment as Usual- Randomized, and Treatment as Usual-Observational/Not Randomized), and the dependent variable was the number of hours worked post-treatment. Supported employment refers to a type of specialized interdisciplinary vocational rehabilitation designed to help people with disabilities obtain and maintain community-based competitive employment in their chosen occupation (Bond, 2004). The null hypothesis is: "There is no difference between the treatment groups in post-treatment number of hours worked among veterans with spinal cord injuries."

Descriptives Hours Worked Per Week 95% Confidence Interval for Mean N Mean Std. Deviation Std. Error Lower Bound Upper Bound Minimum Maximum Treatment as Usual - 5 18.00 3.536 1.581 13.61 22.39 15 24 Observationa Treatment as Usual- 5 18.60 2.702 1.208 15.25 21.95 16 23 Randomized Supported Employment 5 23.40 3.209 1.435 19.42 27.38 19 27 Total 15 20.00 3.854 995 17.87 22.13 15 27 Tests of Homogeneity of Variances Levene Statistic df1 df2 Sig Hours Worked Per Week Based on Mean 130 12 880 Based on Median 095 NNN 12 910 Based on Median and with 095 10.306 910 adjusted df Based on trimmed mean 133 2 12 877 ANOVA Hours Worked Per Week Sum of Squares df Mean Square F Sig. Between Groups 87.600 2 43.800 4.365 038 Within Groups 120.400 12 10.033 Total 208.000 14 ANOVA Effect Sizesab 95% Confidence Interval Point Estimate Lower Upper Hours Worked Per Week Eta-squared 421 000 632 Epsilon-squared 325 .167 570 Omega-squared Fixed- 310 -.154 553 effect Omega-squared Random- 183 .071 383 effect a. Eta-squared and Epsilon-squared are estimated based on the fixed-effect model. b. Negative but less biased estimates are retained, not rounded to zero