Using the Financial Management: Theory & Practice

byEugene F. Brigham, Michael C. Ehrhardt

17th Edition| Copyright 2024

Answer the following: Textbook Assignments:

Chapter 4 : Problems Part (not questions part)

(you can find the problems from Page 151-154 for 17th edition, stilll some students may find these questions in around page 181. TThe Ebook and the hard copy might have different page setting.)

(Note: MO is Module Objective, MO1 means Module Objective 1. The module objectives are listed in the Module Overview for each Module. These are not directly related with the assignments, just letting you know what knowledge point these questions are testing -something required when I designed the class.)

4-1, 4-2, 4-3, 4-4, 4-10 (MO1, 2)

4-8, 4-16, 4-19, 4-32 (MO3, 4)

4-12, 4-13, 4-20, 4-25, 4-26, 4-33 (MO5)

4-14 (MO6)

4-27 (MO7)

Note: Example for necessary steps (if you need to find FV, you need to provide what is PV, N, I etc. That is all is needed.). If you use excel to work on the problems, please copy and paste the related excel contents into Word Document. Don't submit Excel files.

(4-1) Future Value of a Single Payment

If you deposit $10,000 in a bank account that pays 10% interest annually, how much will be in your account after 5 years?

(4-2) Present Value of a Single Payment

What is the present value of a security that will pay $5,000 in 20 years if securities of equal risk pay 7% annually?

(4-3) Interest Rate on a Single Payment

Your parents will retire in 18 years. They currently have $250,000, and they think they will need $1 million at retirement. What annual interest rate must they earn to reach their goal, assuming they don't save any additional funds?

(4-4) Number of Periods of a Single Payment

If you deposit money today in an account that pays 6.5% annual interest, how long will it take to double your money?

(4-5) Number of Periods for an Annuity

You have $42,180.53 in a brokerage account, and you plan to deposit an additional $5,000 at the end of every future year until your account totals $250,000. You expect to earn 12% annually on the account. How many years will it take to reach your goal?

(4-6) Future Value: Ordinary Annuity Versus Annuity Due

What is the future value of a 7%, 5-year ordinary annuity that pays $300 each year? If this were an annuity due, what would its future value be?

(4-7) Present and Future Value of an Uneven Cash Flow Stream

An investment will pay $100 at the end of each of the next 3 years, $200 at the end

of Year 4, $300 at the end of Year 5, and $500 at the end of Year 6. If other invest- ments of equal risk earn 8% annually, what is this investment's present value? Its

future value?

(4-8) Annuity Payment and EAR You want to buy a car, and a local bank will lend you $20,000. The loan would be fully amortized over 5 years (60 months), and the nominal interest rate would be 12%, with interest paid monthly. What is the monthly loan payment? What is the loan's EFF%?

(4-9) Present and Future Values of Single Cash Flows for Different Periods

Find the following values, using the equations, and then work the problems using a financial calculator to check your answers. Disregard rounding differences. (Hint: If you are using a financial calculator, you can enter the known values and then press the appropriate key to find the unknown variable. Then, without clearing the TVM register, you can "override" the variable that changes by simply entering a new value for it and then pressing the key for the unknown variable to obtain the second answer. This procedure can be used in parts b and d, and in many other situations, to see how changes in input variables affect the output variable.) a. An initial $500 compounded for 1 year at 6% b. An initial $500 compounded for 2 years at 6% c. The present value of $500 due in 1 year at a discount rate of 6% d. The present value of $500 due in 2 years at a discount rate of 6%

(4-10) Present and Future Values of Single Cash Flows for Different Interest Rates

Use both the TVM equations and a financial calculator to find the following values. See the Hint for Problem 4-9. a. An initial $500 compounded for 10 years at 6% b. An initial $500 compounded for 10 years at 12% c. The present value of $500 due in 10 years at a 6% discount rate d. The present value of $500 due in 10 years at a 12% discount rate

(4-11) Time for a Lump Sum to Double

To the closest year, how long will it take to double $200 if it is deposited and earns the follow- ing rates? [Notes: (1) See the Hint for Problem 4-9. (2) Some financial calculators will round

up and give an integer answer to the problem, and others will give the exact decimal solution. This problem is asking for the closest integer. For example, if the answer is less than 5.5 years, then round down to 5. If the answer is greater than or equal to 5.5 years, round up to 6.] a. 7% b. 10% c. 18% d. 100%

(4-12) Future Value of an Annuity

Find the future value of the following annuities. The first payment in these annuities is

made at the end of Year 1, so they are ordinary annuities. (Notes: See the Hint to Prob- lem 4-9. Also, note that you can leave values in the TVM register, switch to Begin Mode,

press FV, and find the FV of the annuity due.) a. $400 per year for 10 years at 10% b. $200 per year for 5 years at 5% c. $400 per year for 5 years at 0% d. Now rework parts a, b, and c assuming that payments are made at the beginning of each year; that is, they are annuities due.

(4-13) Present Value of an Annuity

Find the present value of the following ordinary annuities (see the Notes to Problem 4-12): a. $400 per year for 10 years at 10% b. $200 per year for 5 years at 5% c. $400 per year for 5 years at 0% d. Now rework parts a, b, and c assuming that payments are made at the beginning of each year; that is, they are annuities due.

a. Find the present values of the following cash flow streams. The appropriate interest rate is 8%. (Hint: It is fairly easy to work this problem dealing with the individual

cash flows. However, if you have a financial calculator, read the section of the man- ual that describes how to enter cash flows such as the ones in this problem. This will

take a little time, but the investment will pay huge dividends throughout the course. Note that, when working with the calculator's cash flow register, you must enter CF0 5 0. Note also that it is quite easy to work the problem with Excel, using procedures described in the file Ch04 Tool Kit.xlsx.)

Year Cash Stream A Cash Stream B 1 $100 $300 2 400 400 3 400 400 4 400 400 5 300 100 b. What is the value of each cash flow stream at a 0% interest rate?

(4-15) Effective Rate of Interest

Find the interest rate (or rates of return) in each of the following situations: a. You borrow $700 and promise to pay back $749 at the end of 1 year. b. You lend $700 and receive a promise to be paid $749 at the end of 1 year. c. You borrow $85,000 and promise to pay back $201,229 at the end of 10 years. d. You borrow $9,000 and promise to make payments of $2,684.80 at the end of each of the next 5 years.

(4-16) Future Value for Various Compounding Periods Find the amount to which $500 will grow under each of the following conditions: a. 12% compounded annually for 5 years b. 12% compounded semiannually for 5 years c. 12% compounded quarterly for 5 years d. 12% compounded monthly for 5 years (4-17) Present Value for Various Compounding Periods Find the present value of $500 due in the future under each of the following conditions: a. 12% nominal rate, semiannual compounding, discounted back 5 years b. 12% nominal rate, quarterly compounding, discounted back 5 years c. 12% nominal rate, monthly compounding, discounted back 1 year

(4-18) Future Value of an Annuity for Various Compounding Periods

Find the future values of the following ordinary annuities: a. Payments of $400 every 6 months for 5 years at a nominal rate of 12%, compounded semiannually b. Payments of $200 every 3 months for 5 years at a nominal rate of 12%, compounded quarterly c. The annuities described in parts a and b have the same total amount of money paid into them during the 5-year period, and both earn interest at the same nominal rate, yet the annuity in part b earns $101.75 more than the one in part a over the 5 years. Why does this occur?

(4-19) Effective Versus Nominal Interest Rates

Universal Bank pays 7% interest, compounded annually, on time deposits. Regional Bank pays 6% interest, compounded quarterly. a. Based on effective interest rates, in which bank would you prefer to deposit your money?

(4-14) Uneven Cash Flow Stream

184 Part 2 Fixed Income Securities

b. Could your choice of banks be influenced by the fact that you might want to with- draw your funds during the year as opposed to at the end of the year? In answering

this question, assume that funds must be left on deposit during an entire com- pounding period in order for you to receive any interest.

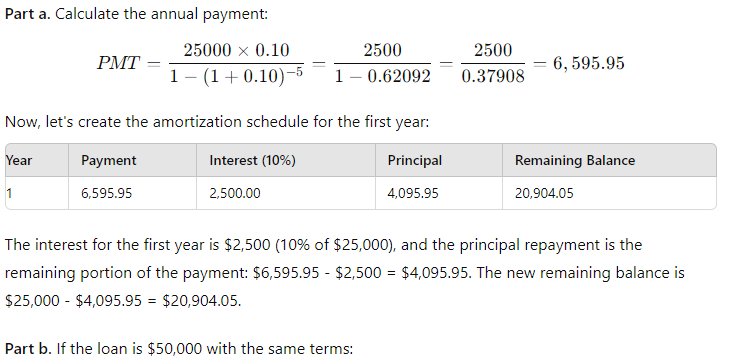
(4-20) Amortization Schedule

Consider a $25,000 loan to be repaid in equal installments at the end of each of the next 5 years. The interest rate is 10%. a. Set up an amortization schedule for the loan. b. How large must each annual payment be if the loan is for $50,000? Assume that the interest rate remains at 10% and that the loan is still paid off over 5 years. c. How large must each payment be if the loan is for $50,000, the interest rate is 10%, and the loan is paid off in equal installments at the end of each of the next 10 years? This loan is for the same amount as the loan in part b, but the payments are spread

out over twice as many periods. Why are these payments not half as large as the pay- ments on the loan in part b?

(4-21) Growth Rates

Sales for Hanebury Corporation's just-ended year were $12 million. Sales were $6 million 5 years earlier. a. At what rate did sales grow? b. Suppose someone calculated the sales growth for Hanebury in part a as follows: "Sales doubled in 5 years. This represents a growth of 100% in 5 years; dividing 100% by 5 results in an estimated growth rate of 20% per year." Explain what is wrong with this calculation.

(4-22) Expected Rate of Return

Washington-Pacific (W-P) invested $4 million to buy a tract of land and plant some young pine trees. The trees can be harvested in 10 years, at which time W-P plans to sell the forest at an expected price of $8 million. What is W-P's expected rate of return?

(4-23) Effective Rate of Interest

A mortgage company offers to lend you $85,000; the loan calls for payments of $8,273.59 at the end of each year for 30 years. What interest rate is the mortgage company charging you?

(4-24)

Required Lump- Sum Payment

To complete your last year in business school and then go through law school, you will need $10,000 per year for 4 years, starting next year (that is, you will need to withdraw the first $10,000 one year from today). Your uncle offers to put you through school, and he will deposit in a bank paying 7% interest a sum of money that is sufficient to provide the four payments of $10,000 each. His deposit will be made today. a. How large must the deposit be? b. How much will be in the account immediately after you make the first withdrawal? After the last withdrawal?

(4-25) Repaying a Loan

While Mary Corens was a student at the University of Tennessee, she borrowed $12,000 in student loans at an annual interest rate of 9%. If Mary repays $1,500 per year, then how long (to the nearest year) will it take her to repay the loan?

(4-26) Reaching a Financial Goal

You need to accumulate $10,000. To do so, you plan to make deposits of $1,250 per yearwith the first payment being made a year from todayinto a bank account that pays 12% annual interest. Your last deposit will be less than $1,250 if less is needed to round out to $10,000. How many years will it take you to reach your $10,000 goal, and how large will the last deposit be?

(4-27) Present Value of a Perpetuity

What is the present value of a perpetuity of $100 per year if the appropriate discount rate is 7%? If interest rates in general were to double and the appropriate discount rate rose to 14%, what would happen to the present value of the perpetuity?

(4-28) PV and Effective Annual Rate

Assume that you inherited some money. A friend of yours is working as an unpaid intern at a local brokerage firm, and her boss is selling securities that call for four payments of $50 (one payment at the end of each of the next 4 years) plus an extra payment of $1,000 at the end of Year 4. Your friend says she can get you some of these securities at a cost of

$900 each. Your money is now invested in a bank that pays an 8% nominal (quoted) inter- est rate but with quarterly compounding. You regard the securities as being just as safe,

and as liquid, as your bank deposit, so your required effective annual rate of return on the

securities is the same as that on your bank deposit. You must calculate the value of the se- curities to decide whether they are a good investment. What is their present value to you?

(Hint: Do not round intermediate calculations to less than six decimal places.)

(4-29) Loan Amortization

Assume that your aunt sold her house on December 31, and to help close the sale she took a second mortgage in the amount of $10,000 as part of the payment. The mortgage has a quoted (or nominal) interest rate of 10%; it calls for payments every 6 months, beginning on June 30, and is to be amortized over 10 years. Now, 1 year later, your aunt must inform the IRS and the person who bought the house about the interest that was included in the two payments made during the year. (This interest will be income to your aunt and a deduction to the buyer of the house.) a. To the closest dollar, what is the remaining balance at the end of the first year? b. To the closest dollar, what is the total amount of interest that was paid during the first year? (4-30) Loan Amortization

Your company is planning to borrow $1 million on a 5-year, 15%, annual payment, fully amortized term loan. What fraction of the payment made at the end of the second year will represent repayment of principal?

(4-31) Nonannual Compounding

It is now January 1. You plan to make a total of five deposits of $100 each, one every 6 months, with the first payment being made today. The bank pays a nominal interest rate of 12% but uses semiannual compounding. You plan to leave the money in the bank for 10 years. a. How much will be in your account after 10 years?

b. You must make a payment of $1,432.02 in 10 years. To get the money for this pay- ment, you will make five equal deposits, beginning today and for the following four

quarters, in a bank that pays a nominal interest rate of 12% with quarterly com- pounding. How large must each of the five payments be?

(4-32) Nominal Rate of Return

Anne Lockwood, manager of Oaks Mall Jewelry, wants to sell on credit, giving custom- ers 3 months to pay. However, Anne will have to borrow from her bank to carry the

accounts receivable. The bank will charge a nominal rate of 15% and will compound monthly. Anne wants to quote a nominal rate to her customers (all of whom are expected to pay on time) that will exactly offset her financing costs. What nominal annual rate should she quote to her credit customers?

4-33. Assume that your father is now 50 years old, plans to retire in 10 years, and expects to live for 25 years after he retiresthat is, until age 85. He wants his first retirement payment to have the same purchasing power at the time he retires as $40,000 has today. He wants all of his subsequent retirement payments to be equal to his first retirement payment. (Do not let the retirement payments grow with inflation: Your father realizes that if inflation occurs the real value of his retirement income will decline year by year after he retires.) His retirement income will begin the day he retires, 10 years from today, and he will then receive 24 additional annual payments. Inflation is expected to be 5% per year from today forward. He currently has $100,000 saved and expects to earn a return on his savings of

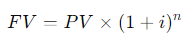
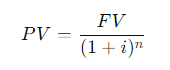
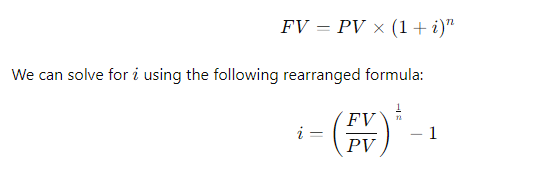
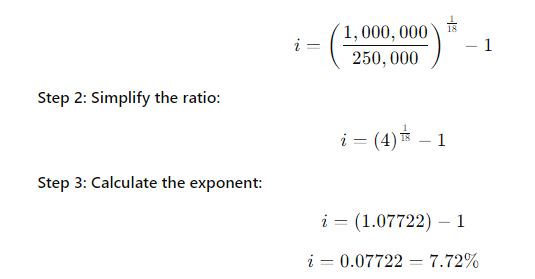
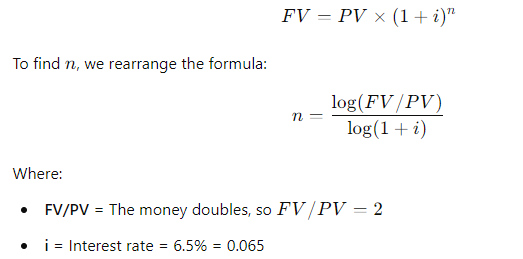
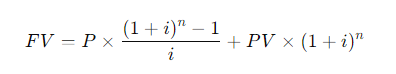
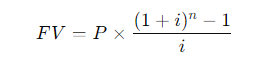
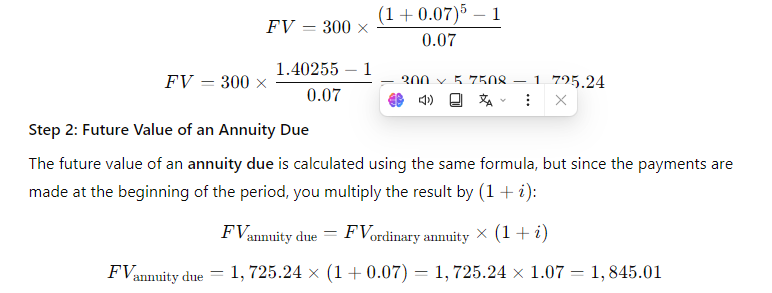
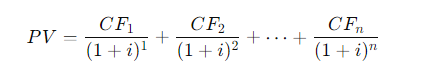
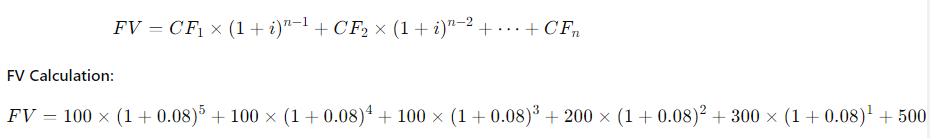
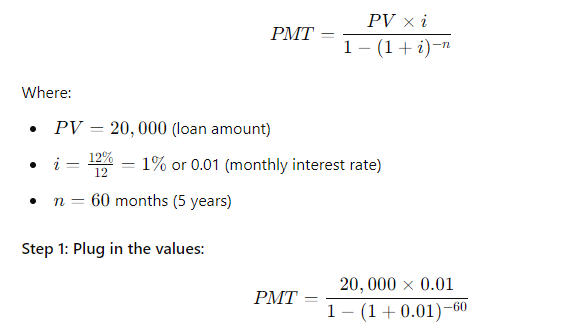
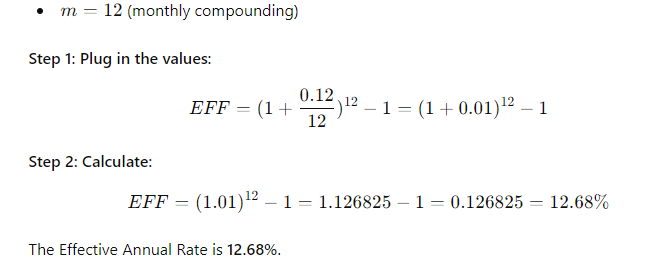
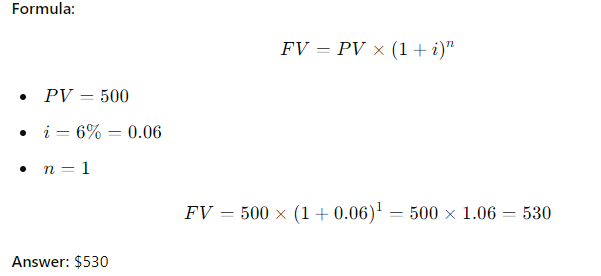
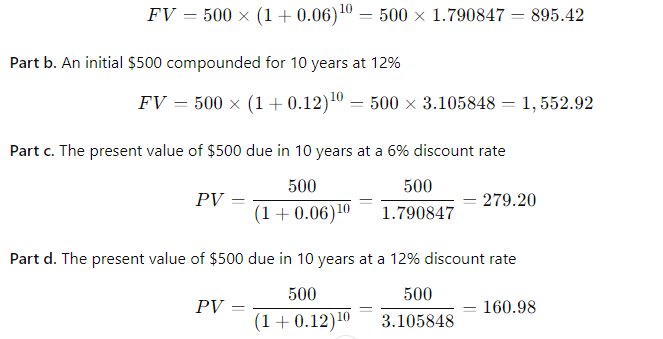
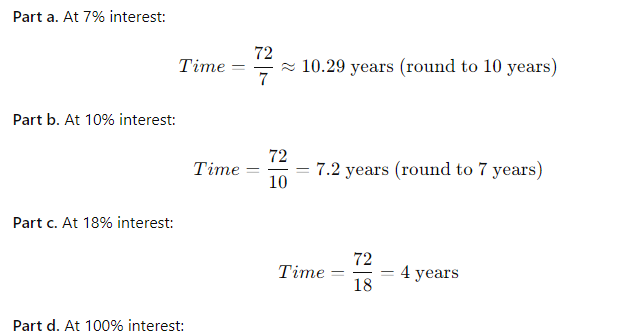
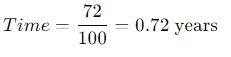
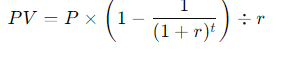
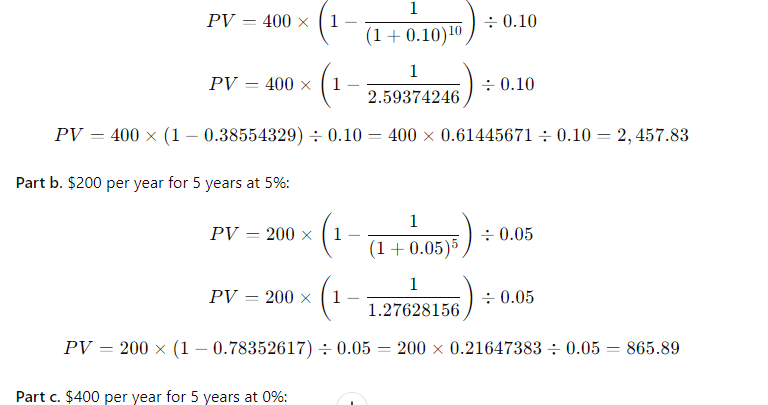
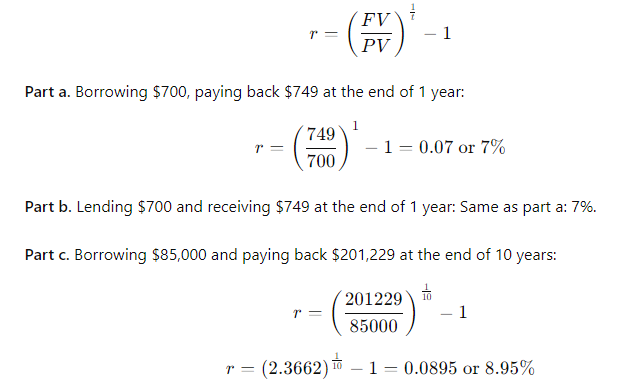
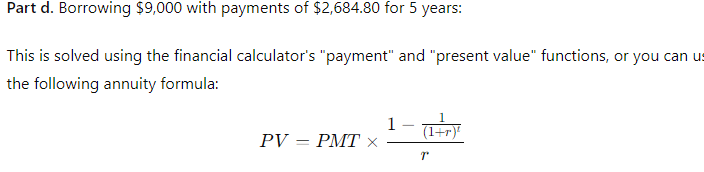
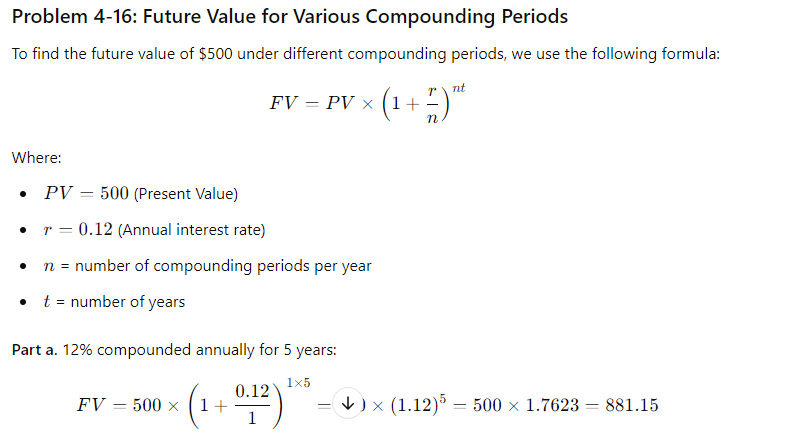
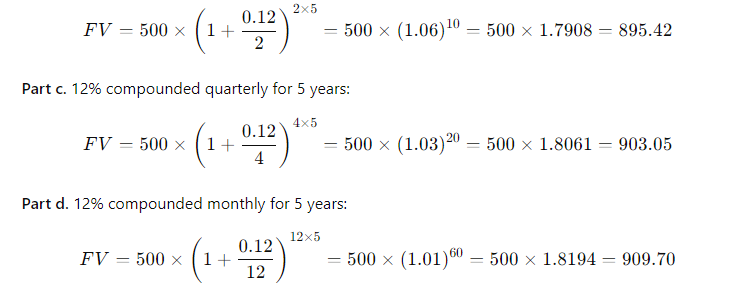
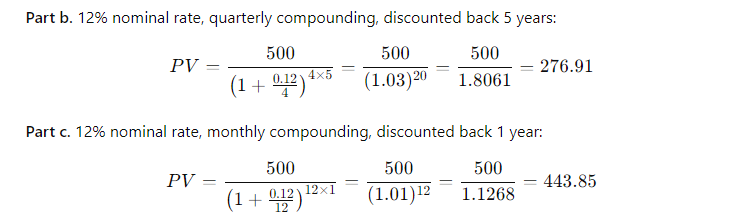
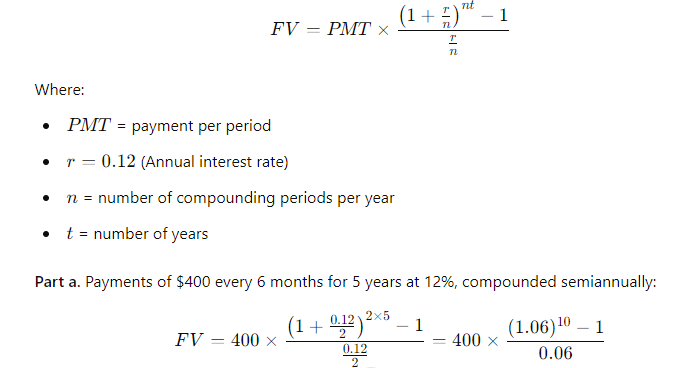
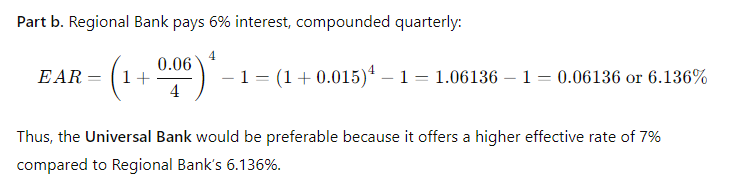
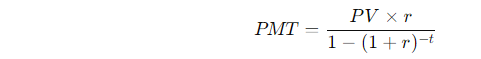
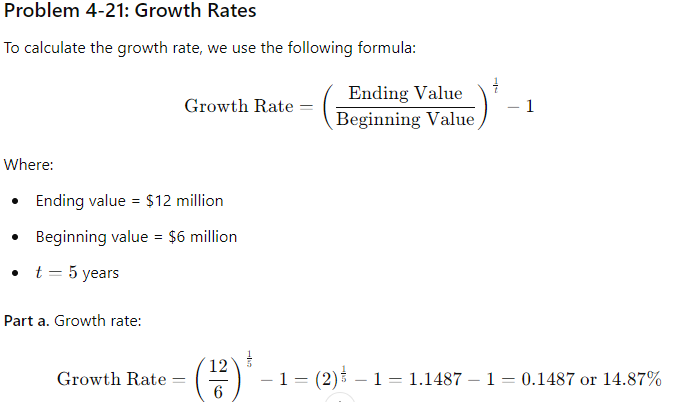
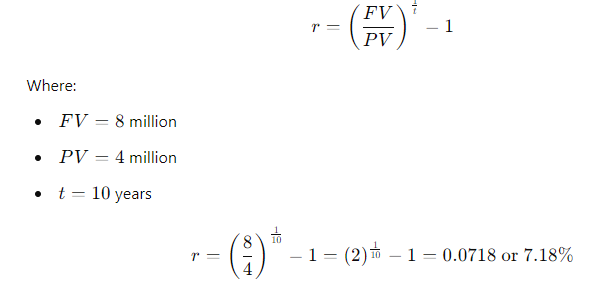
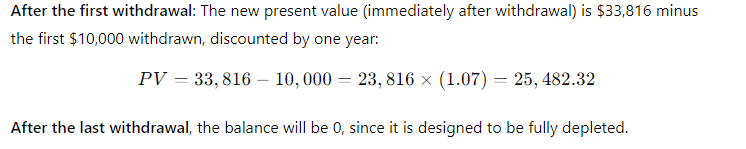
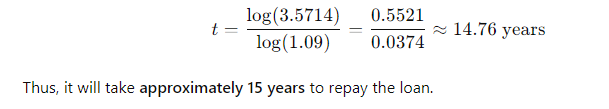
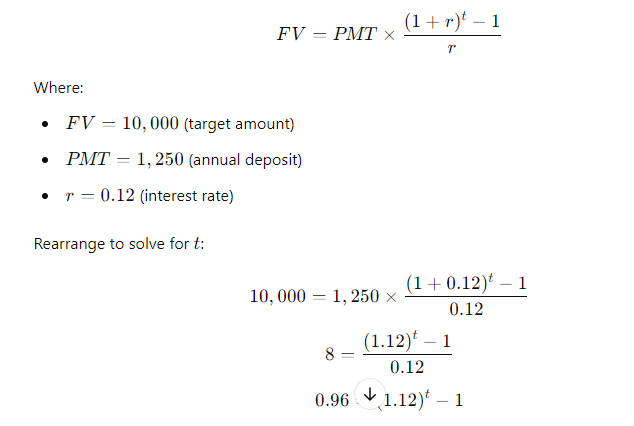
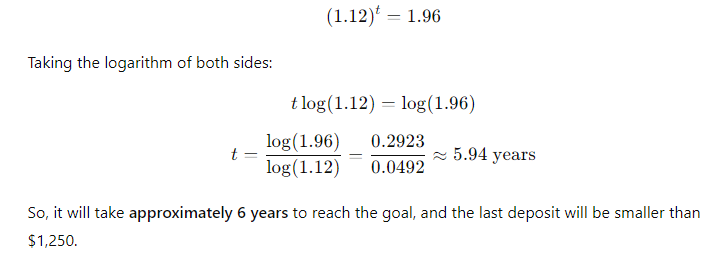
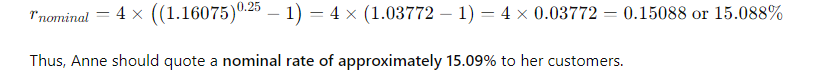
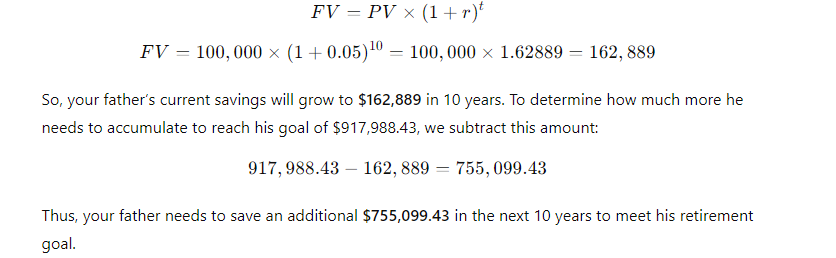\fFV - 10, 000 x (1 + 0.10)5 . 1 +0.10 = 1.10 . So, the formula becomes: FV = 10, 000 x (1.10)5 Step 4: Calculating (1.10)5 Next, we need to calculate (1.10)". This means multiplying 1.10 by itself 5 times: (1.10) = 1.10 x 1.10 x 1.10 x 1.10 x 1.10 Using a calculator: (1.10)" = 1.61051FV PV 1 + 2)\fFV - PV x (1+i)n We can solve for i using the following rearranged formula: FV = - 1 PV1, 000, 000 1 = - - 250, 000 Step 2: Simplify the ratio: i - (4) 18 - 1 Step 3: Calculate the exponent: i = (1.07722) - 1 i = 0.07722 - 7.72%FV - PV x (1+i)" To find n, we rearrange the formula: log (FV / PV) n= log (1 + 2) Where: FV/PV = The money doubles, so FV / PV = 2 . i = Interest rate = 6.5% = 0.065Step 1: Plug in the values: log(2) i log(1.065) Step 2: Calculate the logarithms: ~0.3010 0.0275 Step 3: Solve for n: n 10.94 years (1 +i)" - 1 FV - PX | PV x (1+i)\f(1 + 0.07) - 1 FV = 300 X 0.07 1.40255 - 1 FV = 300 X 200 v 5 7508 - 1 795.24 0.07 X Step 2: Future Value of an Annuity Due The future value of an annuity due is calculated using the same formula, but since the payments are made at the beginning of the period, you multiply the result by (1 + i): FVannuity due = FVordinary annuity X (1 + 2) FVannuity due - 1, 725.24 x (1 + 0.07) - 1, 725.24 x 1.07 = 1, 845.01\f\f\fPV xi PMT = 1 - (1 +i)-n Where: . PV = 20, 000 (loan amount) . i = 12% 12 - 1% or 0.01 (monthly interest rate) . n = 60 months (5 years) Step 1: Plug in the values: 20, 000 x 0.01 PMT = 1 - (1 + 0.01) -60Step 2: Simplify the denominator: 200 200 PMT = 1 - (1.01)-60 1 - 0.55368 200 PMT 448.88 0.44632 The monthly loan payment is $448.88. 2. Effective Annual Rate (EFF%): The Effective Annual Rate (EAR) can be calculated using the following formula: EFF - (1+ Nominal Rate m - 1 Where: . Nominal Rate = 12% or 0.12e m 12 {(monthly compounding) Step 1: Plug in the values: 0.12 12 EFF (1 + 1= (14001 -1 Step 2: Calculate: EFF = (1.01)"* 1 = 1.126825 1 0.126825 12.68% The Effective Annual Rate is 12.68%. Formula: FV - PV x (1+i)" . PV = 500 . i - 6% = 0.06 . n = 1 FV - 500 x (1 + 0.06) = 500 x 1.06 = 530 Answer: $530FV - 500 x (1 + 0.06) - 500 x 1.790847 - 895.42 Part b. An initial $500 compounded for 10 years at 12% FV - 500 x (1 + 0.12) = 500 x 3.105848 - 1, 552.92 Part c. The present value of $500 due in 10 years at a 6% discount rate 500 500 PV 279.20 (1 + 0.06) 10 1.790847 Part d. The present value of $500 due in 10 years at a 12% discount rate 500 500 PV = = 160.98 (1 + 0.12) 10 3.105848Part a. At 7% interest: : 72 Time = T 10.29 years (round to 10 years) Part b. At 10% interest: Time i = 7.2 years (round to 7 years) Part c. At 18% interest: 72 Time W' 4 years Part d. At 100% interest: \f\f1 PV = 400 X 1 : 0.10 (1 + 0.10) 10 1 PV - 400 x 1 - : 0.10 2.59374246 PV - 400 x (1 - 0.38554329) : 0.10 = 400 x 0.61445671 : 0.10 = 2, 457.83 Part b. $200 per year for 5 years at 5%: 1 PV = 200 X 1 : 0.05 (1 + 0.05)5 PV = 200 x 1 : 0.05 1.27628156 PV - 200 x (1 - 0.78352617) : 0.05 - 200 x 0.21647383 + 0.05 = 865.89 Part c. $400 per year for 5 years at 0%:PV = 400 x 5 = 2, 000 (With 0% interest, the present value is just the sum of the payments.) Part d. Rework parts a, b, and c assuming that payments are made at the beginning of each year (annuities due): For annuities due, the present value is calculated as follows: PVdue = PVordinary X (1 + r) . For part a: PVdue - 2, 457.83 x (1 + 0.10) - 2, 703.61 For part b.. For part b: PVdue - 865.89 x (1 + 0.05) = 909.18 . For part c (since there's no interest rate, the present value stays the same): PVdue = 2, 000Cash Flow Streams (4-14) Part a. Find the present values of the following cash flow streams at an 8% discount rate: For Cash Stream A: 100 400 400 400 300 PV= (11008 (110082 @ (110.08 (11008 (L1008 Calculating each term: ~ 100 400 400 400 L 300 1.08 1.1664 1.2597 1.3605 1.4693 PV = 92.59 + 342.97 + 317.57 + 293.92 + 204.18 1, 251.23 PV For Cash Stream B: For Cash Stream B: 300 400 400 400 100 py >~ =7 . 7 "7 7 (17008 (110082 (110087 (14008 (1+0.08)p Calculating each term: ~ 300 400 400 400 . 100 1.08 1.1664 1.2597 1.3605 1.4693 PV = 277.78 + 342.97 + 317.57 + 293.92 + 68.09 = 1, 300.33 PV Part b. At a 0% interest rate, the present value is just the sum of the cash flows: e (Cash Stream A: 5100 + $400 + 3400 + $400 + 5300 = 1,600 (Cash Stream B: $300 + $400 + $400 + $400 + $100 = 1,600 _(EVY | ! PV Part a. Borrowing $700, paying back $749 at the end of 1 year: 749\\ ! r (222} 1 007To0r7 " (?l}) or 7% Part b. Lending $700 and receiving $749 at the end of 1 year: Same as part a: 7%. Part c. Borrowing $85,000 and paying back $201,229 at the end of 10 years: 201229\\ T - - 85000 r = (2.3662)T 1 = 0.0895 or 8.95% Part d. Borrowing $9,000 with payments of $2,684.80 for 5 years: This is solved using the financial calculator's "payment" and "present value" functions, or you can u the following annuity formula: 1 - (1+r) PV - PMT XProblem 4-16: Future Value for Various Compounding Periods To find the future value of $500 under different compounding periods, we use the following formula: oo Tit FV PV (1 + ) T Where: e PV 500 (Present Value) e 7 (.12 (Annual interest rate) * 1 = number of compounding periods per year e { = number of years Part a. 12% compounded annually for 5 years: 2 0.12)\\ " i FV = 500 x (1 + T) ) x (1.12) = 500 x 1.7623 = 881.15 \fProblem 4-17: Present Value for Various Compounding Periods To find the present value, we use the formula: FVv PV - (1+7) Where: e F'V 500 (Future Value) e 7 (.12 (Annual interest rate) * 1. = number of compounding periods per year e { = number of years Part a. 12% nominal rate, semiannual compounding, discounted back 5 years: 500 500 500 PV = .12y 278 1.06)10 : (1 1 & ) 'LLDIE}) 1.7908 = 279.20 Part b. 12% nominal rate, quarterly compounding, discounted back 5 years: 500 500 500 (1+22)" (L03) 1.8061 Part c. 12% nominal rate, monthly compounding, discounted back 1 year: 500 500 500 PV - - T _ 44385 (1 + 12) - (L.01)12 1.1268 (1+1 nit - 1 FV - PMT X Where: . PMT = payment per period . " = 0.12 (Annual interest rate) . n = number of compounding periods per year . t = number of years Part a. Payments of $400 every 6 months for 5 years at 12%, compounded semiannually: 1 0.12 2x5 1 (1.06)10 - 1 FV = 400 X 2 = 400 x 0.12 0.06 21.7908 1 FV =400 x YT 400 = 13.1807 = 5,272.28 06 Part b. Payments of $200 every 3 months for 5 years at 12%, compounded quarterly: Fv 00 L b7 200 x 103"~ 1 f = - fmai1s = & w - o 0.03 1.8061 1 FV =200 x 200 x 26.8695 5, 373.90 0.03 Part c. The annuity in part b earns $101.75 more than the one in part a due to the increased frequency of compounding. In part b, interest is compounded quarterly, which allows the interest to accumulate faster compared to semiannual compounding in part a. Even though the total amount deposited is the same, the more frequent compounding leads to higher growth. Problem 4-19: Effective Versus Nominal Interest Rates To compare effective interest rates, we use the following formula for the Effective Annual Rate (EAR): T ' EAR= (1+-) 1 n Where: s 1 = nominal interest rate * 1 = number of compounding periods per year Part a. Universal Bank pays 7% interest, compounded annually: 0.07\\* E.&R = (l -+ T) l = H.UT or T{:'(EJ Since it is compounded annually, the effective - -4 nominal rates are the same. Part b. Regional Bank pays 6% interest, compounded quarterly: 0.06 4 EAR = 1 - 1 = (1 + 0.015)* - 1 - 1.06136 -1 = 0.06136 or 6.136% Thus, the Universal Bank would be preferable because it offers a higher effective rate of 7% compared to Regional Bank's 6.136%.\fPart a. Calculate the annual payment: 25000 % 0.10 2500 2500 pMT - " S T 505.05 I (1+0.10) 106292 037908 " Mow, let's create the amortization schedule for the first year: Year Payment Interest (10%) Principal Remaining Balance 1 2,595.95 2,500.00 4,0595.95 20,904.05 The interest for the first year is $2,500 (10% of $25,000), and the principal repayment is the remaining portion of the payment: $6,595.95 - $2,500 = $4,095.95. The new remaining balance is 525,000 - $4,095.95 = $20,904.05. Part b. If the lcan is $50,000 with the same terms: 50000 = 0.10 5000 PMT = = 13,191.90 I (1+40.10)= 0.37908 ' Part c. If the loan is for $50,000, with a 10-year repayment period: AT 50000 = 0.10 _ 5000 5000 _8.136.85 1(1+0.10)"0 1-0.38554 0.61446 Even though the repayment period is doubled, the payments are not halved because more interest accumulates over time. Problem 4-21: Growth Rates To calculate the growth rate, we use the following formula: Growth Rate = Ending Value - 1 Beginning Value Where: . Ending value = $12 million . Beginning value = $6 million . t = 5 years Part a. Growth rate: Growth Rate = - 1 = (2)3 -1 = 1.1487 -1 = 0.1487 or 14.87%FV T = - 1 PV Where: . FV = 8 million . PV = 4 million . t = 10 years To T= -1 - (2) 10 - 1 - 0.0718 or 7.18%L (1+7)" T PV = PMT x Rearranging to solve for r, this problem is best solved using a financial calculator, as the equation involves iterative calculations. You can enter the following into a financial calculator: o PV 85,000 o PMT ,273.59 o t30 This will give you an interest rate close to 9%. PV - PMT X 1 - (1+r)- T' Where: . PMT = 10, 000 . r = 0.07 . t =4 1 - (1 + 0.07)-4 1 - 0.7629 PV = 10, 000 X = 10, 000 X = 10, 000 x 3.3816 - 33, 816 0.07 0.07 The uncle must deposit $33,816 today.After the first withdrawal: The new present value (immediately after withdrawal) is $33,816 minus the first $10,000 withdrawn, discounted by one year: PV = 33,816 10,000 = 23,816 x (1.07) = 25,482.32 After the last withdrawal, the balance will be 0, since it is designed to be fully depleted. log PMT PMT-rxPV t = log (1 + r) Where: . PMT - 1, 500 (annual payment) . " = 0.09 (annual interest rate) . PV = 12, 000 (loan amount) log 1500 log 1500 1500 1500-0.09x12000 1500-1080 log 420 t = log(1 + 0.09) log (1.09) log (1.09log(3.5714) 0.5521 log(1.09) 0.0374 ~ 14.76 years Thus, it will take approximately 15 years to repay the loan. FV - PMT X (1+r)* - 1 Where: . FV - 10, 000 (target amount) . PMT - 1, 250 (annual deposit) . r = 0.12 (interest rate) Rearrange to solve for t: (1 + 0.12) - 1 10, 000 = 1, 250 X 0.12 (1.12 )* - 1 8 - 0.12 0.96 1.12)* - 1(1.12) = 1.96 Taking the logarithm of both sides; t log(1.12) - log (1.96) log (1.96) 0.2923 t = log (1.12) 0.0492 ~ 5.94 years So, it will take approximately 6 years to reach the goal, and the last deposit will be smaller than $1,250.Problem 4-27: Present Value of a Perpetuity The present value of a perpetuity is calculated using the formula: PMT PV = Where: . PMT = 100 (annual payment) . " = 0.07 (discount rate) 100 PV = - 1, 428.57 0.07 If the discount rate rises to 14%: 100 PV = 714.29 0.141 0.08 EAR (l + T) 1 1.082432 1 0.082432 or 8.2432% Next, we calculate the present value (PV) of the security with 4 payments of $50 and a final payment of $1,000 at the end of Year 4. The formula for the present value of cash flows is: 50 50 () 1050 PV = (11 EAR) ' (1+ EAR? (1+ EAR) (11 EAR) Substituting values: a0 . 5() . 50 1050 1.082432 1.0824322 ' 1.0824323 = 1.082432% PV = 46.18 + 42.67 + 39.40 + 760.84 889.09 - PV XT PMT = 1 - (1+r)-t Where: . PV = 10, 000 " = 2 0.10 - 0.05 . t = 20 (10 years x 2) 10, 000 x 0.05 500 500 PMT 802.76 1 - (1 + 0.05)-20 1 - 0.37689 0.62311 The remaining balance after one year (2 payments) can be calculated by subtracting the principal portion of the payments. Part b. Total interest paid in the first year: For *first two payments, calculate the interest portionFV - PMT x (1+r/ n)nt - 1 r Where: . PMT = 100 . r = 0.12 . n = 2 (semiannual) . t = 10 Part b. Payment size needed for the lump sum payment: Use the present value of a lump sum formula to calculate the necessary payment size.0.15 12 EAR = 1 + - 1 - (1 + 0.0125) 12 - 1 12 EAR - (1.0125) 2 - 1 - 1.16075 -1 = 0.16075 or 16.075% Step 2: Nominal Rate for Customers Now, Anne needs to quote a nominal rate that, when compounded quarterly (since customers have 3 months to pay), would match the 16.075% EAR. We use the formula: Tnominal = n X ((1 + EAR) 1/ - 1) Where: . n = 4 (quarterly compounding) "nominal - 4 x ((1 + 0.16075 ) 1/4 - 1)"nominal = 4 X ((1.16075)".2 - 1) - 4 x (1.03772 - 1) - 4 x 0.03772 - 0.15088 or 15.088% Thus, Anne should quote a nominal rate of approximately 15.09% to her customers.FV - PV x (1+i)* Where: . PV = 40, 000 (current value) . i = 0.05 (annual inflation rate) . t = 10 (years) FV = 40, 000 x (1 + 0.05) = 40, 000 x 1.62889 - 65, 155.60 Thus, your father's first retirement payment must be $65,155.60 to match the purchasing power of $40,000 today.1 - (1+r)t PV - PMT X Where: . PMT - 65, 155.60 (adjusted retirement payment) . r = rate of return on savings (assuming it is the same as inflation at 5%) . t = 25 (number of payments) Assuming r = 0.05 (5% return), the present value needed at the start of retirement would be: 1 - (1 + 0.05)-25 PV - 65, 155.60 X 0.05 1 - 0.29530: 4 PV - 65, 155.60 x 65, 155.60 x 14.09396 - 917, 988.43 0.05FV = PV x (1 +7) FV = 100,000 x (1 +0.05)" = 100,000 x 1.62889 162, 889 So, your father's current savings will grow to $162,889 in 10 years. To determine how much more he needs to accumulate to reach his goal of $917,988.43, we subtract this amount: 917,988.43 162, 889 755,099.43 Thus, your father needs to save an additional $755,099.43 in the next 10 years to meet his retirement goal