Using the model developed in The Economy Unit 3, Section 3.7, consider Ella who is a personal trainer at a popular gym in Sydney. Prior to the coronavirus pandemic she had been receiving a wage of $40 per hour.

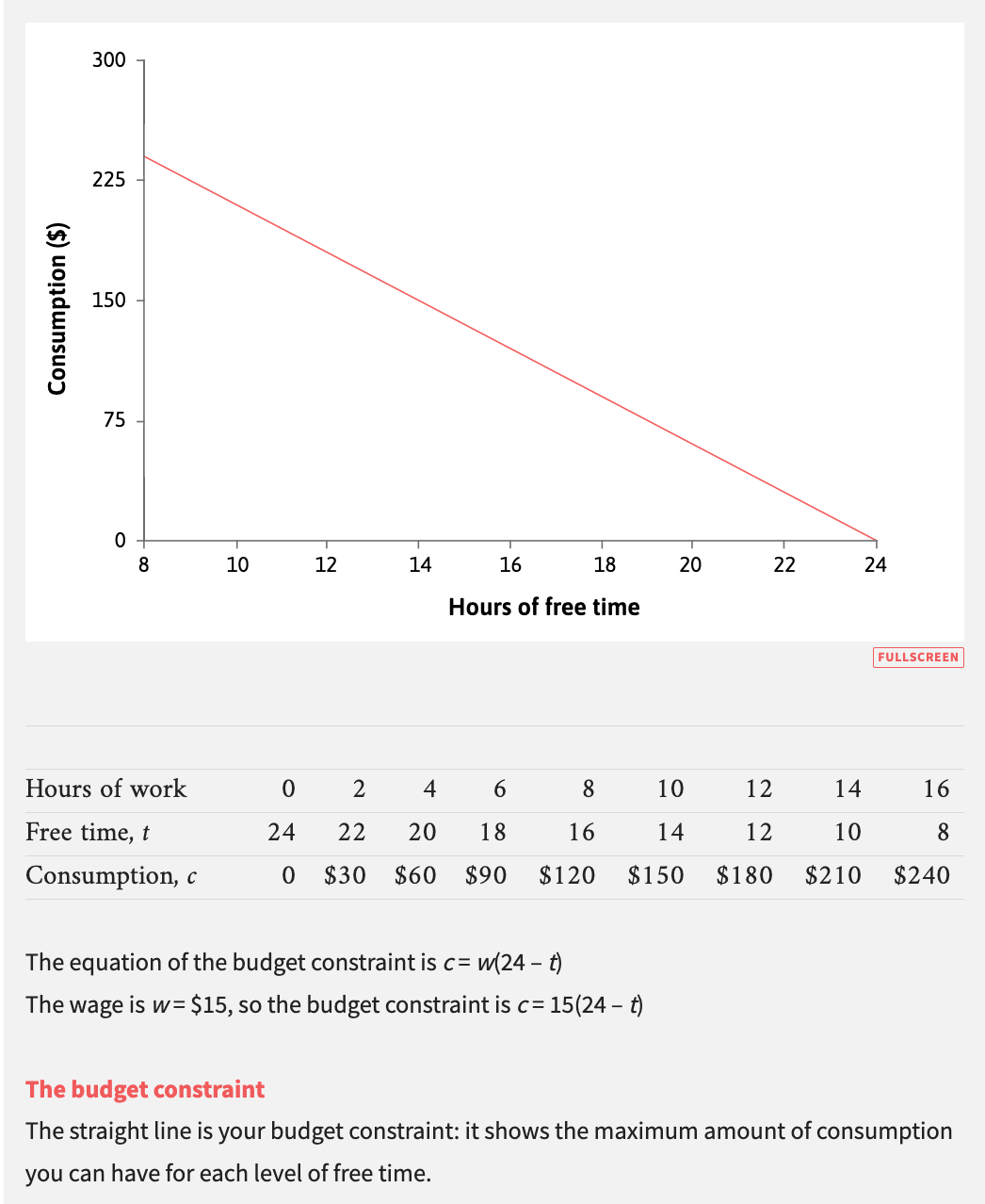
Assume that Ella's spending on goods and services cannot exceed her earnings per day. Maximum consumption (c) per day is:

c = w(24 - t) where t = hours of free time per day.

Your answers must include both a diagram and words to clearly explain your diagram. In addition, your diagram must be fully labelled and therefore you must label both axes, correctly determine the vertical axis and horizontal axis intercepts, label the slope of the budget constraint and show the optimal amount of free time and consumption associated with it.

a. Initially when facing w = $40 per hour Ella chooses to work 8 hours per day and have 16 hours of free time per day. Using a fully labelled diagram describe Ella's utility maximizing combination of free time and consumption. (4 marks)

b. Due to the financial impact of the coronavirus on the gym, the owners of the gym have reduced Ella's wage to $30 per hour. Using the same diagram as used in part "a" show Ella's new utility maximizing combination of free time and spending on goods and services assuming that her hours of free time each day decrease to 12 hours. (4 marks)

c. On your diagram decompose the overall change in hours of free time in response to the wage decrease into the (i) income effect and (ii) substitution effect. You must use words as well as the diagram to explain the decomposition of the overall change. (7 marks)

300 225 E c .2 '5. 150 E 3 E O U 75 0 8 10 12 l4 16 18 20 22 24 Hours of free time Hours of work 0 2 4 6 8 10 12 14 16 Free time, t 24 22 20 18 16 14 12 10 8 Consumption,c 0 $30 $60 $90 $120 $150 $180 $210 $240 The equation ofthe budget constraint is C: W(24 t) The wage is W: 515, so the budget constraint is C: 15(24 t) The budget constraint The straight line is your budget constraint: it shows the maximum amount of consumption you can have for each level of free time