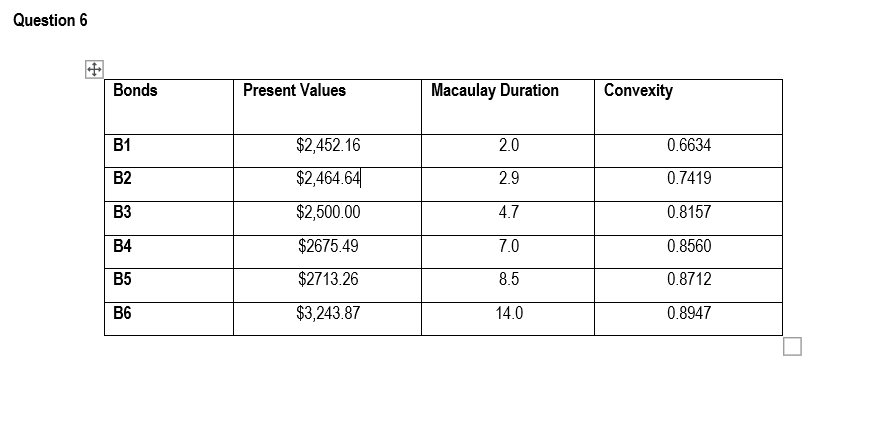
Using the table above and the information provided solve the following question

Let Wi be the amount of bond I purchase, the objective is minimize the transactions costs associated with buying the 6 type of bonds. To achieve this the fund manager aims to minimize the total number of bonds they purchase. The objective function that we will use is Z= 1N1+1N2+1N3+1N14+1N5+1N6

The first condition for immunization is that the value of the bonds purchase i.e. the product of the price and the number of bonds , must equal to the present value of the future payments that must be made. This equality constraint is written in the following way

PV Payments = PVB1.N1+PV B2. N2+PVB3.1N3+PV.B4.N14+PV.B5.N5+PV B6.N6

The second condition is that the duration of the bond portfolio is equal to the duration of the future payments, to find the duration of the bond portfolio we use a weighted average of the durations of the individual bonds. The weight for any bond is equal to the share of the value of the bond in the value of the portfolio. Since the value of the bond is equal to the product of its price and the number of bonds the weight for first bond is

W1 = PV B1N1PV Payments (MD B1)+W2(MD B2)+W3(MDB3)+W4(MDB4)+W5(MD B5)+W6(MDB6).

Also needed diversification constraint

N1 6 , N2 6, N3 6 , N4 6 ,N56.

QUESTION

8 (use Excel to do this question) For the portfolio described in QUESTIONS 6 and 7 and the methods outlined in the course notes on Mathematical Programming; that is, using the solver in excel, find the portfolio of bonds that the fund manager must invest in to immunize the portfolio. That is, the two streams of payments and receipts need to have the same Present Value, their Macaulay Durations must be equal, the diversification conditions should be satisfied and the Convexityreceipts (Assets) needs to be greater than the Convexitypayments (Liabilities). However, finding the immunized portfolio should be done in stages reporting the different number bonds held at each step: (i) The stream of payments and receipts need to have the same Present Value. (ii) Add the constraint that the Macaulay Durations must be equal. (iii) Now include the diversification condition of holding a minimum of five of each bond. (iv) Lastly, include the second order condition of Convexityreceipts > Convexitypayments, so that all four constraints are now being applied. Write a brief paragraph explaining how much of each bond the fund manager should hold and how this changes as each constraint was added. Please submit you answer and sensitivity reports for step (iv) only.

Question 6 Bonds Present Values Macaulay Duration Convexity B1 2.0 0.6634 B2 $2,452.16 $2,464.64 $2,500.00 2.9 0.7419 B3 4.7 0.8157 B4 $2675.49 7.0 0.8560 B5 $2713.26 8.5 0.8712 B6 $3,243.87 14.0 0.8947 Question 6 Bonds Present Values Macaulay Duration Convexity B1 2.0 0.6634 B2 $2,452.16 $2,464.64 $2,500.00 2.9 0.7419 B3 4.7 0.8157 B4 $2675.49 7.0 0.8560 B5 $2713.26 8.5 0.8712 B6 $3,243.87 14.0 0.8947