Answered step by step
Verified Expert Solution
Question
1 Approved Answer
#!/usr/bin/env python import math as m import numpy as np def main(): # Length of each links for the planar 3R robot l1 = 5
#!/usr/bin/env python import math as m import numpy as np def main(): # Length of each links for the planar 3R robot l1 = 5 l2 = 7 l3 = 2 # Given the following transformation from 0 to P: T0_P = np.mat([[-0.5, -0.8660254, 0, 5.34327225], [0.8660254, -0.5, 0, 10.6066229], [0, 0, 1, 0], [0, 0, 0, 1]]) # Find at least 2 solutions sets [theta_1, theta_2, theta_3] for the robot # manipulator position. # Use IK formulas learned from the lecture. # Get the x, y coordinate from T0_P: x, y = ###CODE#HERE### print('x, y coord: {},{}'.format(x,y)) # If surprised by the order here, it is recommended to review the lecture. # You are welcome to add as many intermediate steps as you judge necessary. #_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_# # Here starts the calculations for the first set of solutions: print(" Solution 1: ") # Theta 2 cos_theta_2 = ###CODE#HERE### print("Cosinus Theta 2: {}".format(cos_theta_2)) sin_theta_2 = ###CODE#HERE### print("Sinus Theta 2: {}".format(sin_theta_2)) theta_2 = ###CODE#HERE### # Theta 1 k1 = ###CODE#HERE### k2 = ###CODE#HERE### theta_1 = ###CODE#HERE### # Theta 3 phi = ###CODE#HERE### print("Phi: {}".format(m.degrees(phi))) theta_3 = ###CODE#HERE### # 1st set of solution with angles converted to degrees solution_1 = [m.degrees(theta_1), m.degrees(theta_2), m.degrees(theta_3)] print("Theta 1, 2, and 3: {}".format(solution_1)) #_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_*-*_# # Here starts the calculations for the second set of solutions: print(" Solution 2: ") # Theta 2 cos_theta_2 = ###CODE#HERE### print("Cosinus Theta 2: {}".format(cos_theta_2)) sin_theta_2 = ###CODE#HERE### print("Sinus Theta 2: {}".format(sin_theta_2)) theta_2 = ###CODE#HERE### # Theta 1 k1 = ###CODE#HERE### k2 = ###CODE#HERE### theta_1 = ###CODE#HERE### # Theta 3 phi = ###CODE#HERE### print("Phi: {}".format(m.degrees(phi))) theta_3 = ###CODE#HERE### # 2nd set of solution with angles converted to degrees solution_2 = [m.degrees(theta_1), m.degrees(theta_2), m.degrees(theta_3)] print("Theta 1, 2, and 3: {}".format(solution_2)) if __name__ == '__main__': main()The goal is given a Transformation T0_P, find at least two solutions sets [theta_1, theta_2, theta_3] for the robot manipulator x, y position.
We are using a planar 3 revolute joints robot that is identical to the example given in the lecture.
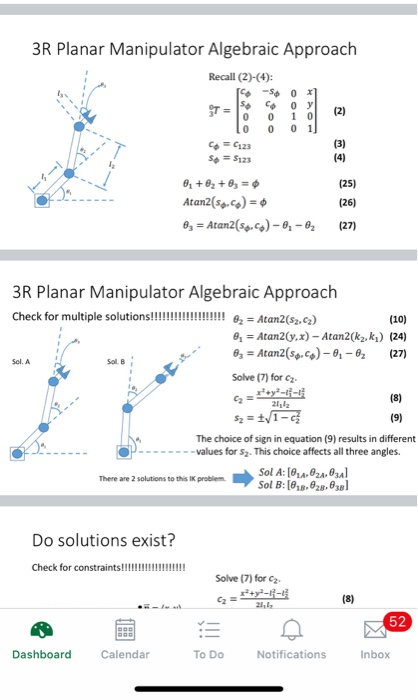
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


