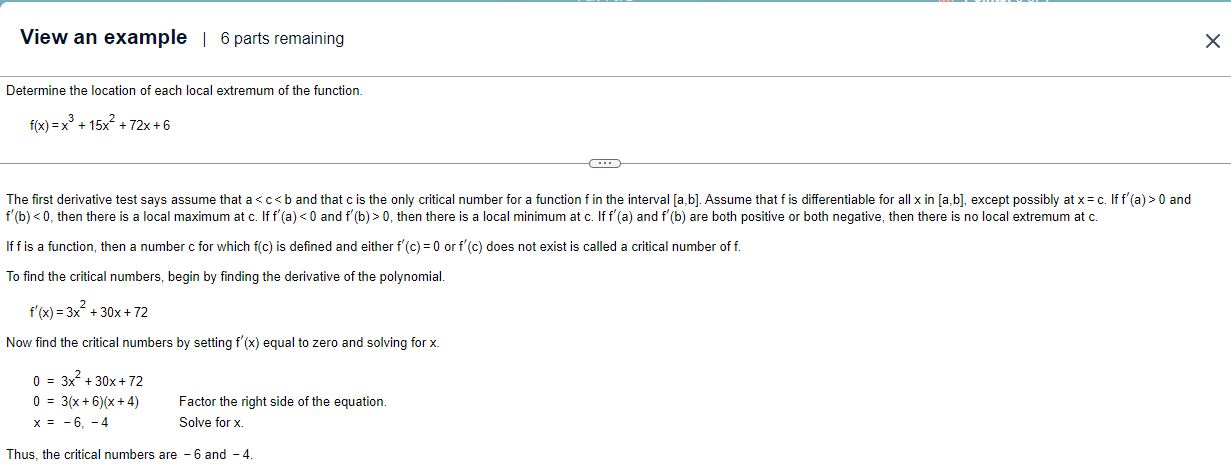
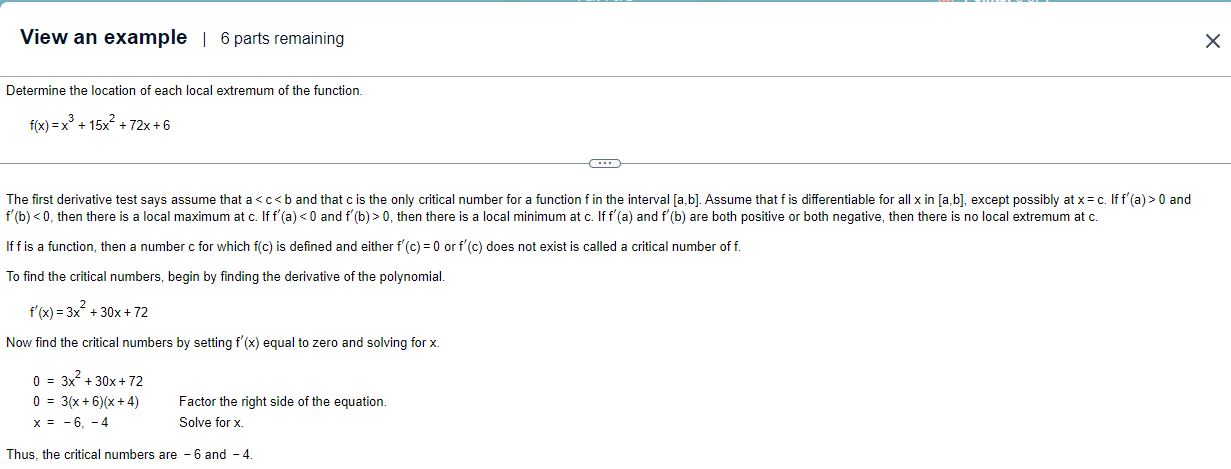
View an example | 6 parts remaining Determine the location of each local extremum of the function. f(x)=x+15x+72x+6 The first derivative test says assume that a 0, then there is a local minimum at c. If f'(a) and f'(b) are both positive or both negative, then there is no local extremum at c. If f is a function, then a number c for which f(c) is defined and either f'(c) = 0 or f'(c) does not exist is called a critical number of f. To find the critical numbers, begin by finding the derivative of the polynomial. f'(x) = 3x + 30x + 72 Now find the critical numbers by setting f'(x) equal to zero and solving for x. 0 = 3x + 30x+72 0 = 3(x+6)(x+4) x = -6, -4 Factor the right side of the equation. Solve for x. Thus, the critical numbers are -6 and -4.