watch the three short clips below then answer the questions

Copy and paste the three links below

1) Projectile Motion

https://www.nsf.govews/mmg/mmg_disp.jsp?med_id=72205&from=

2) Newton's Second Law of Motion

https://www.nsf.govews/mmg/mmg_disp.jsp?med_id=71011&from=

3) Center of Mass

https://www.thirteen.org/programs/circus/circus-circus-physics-center-of-mass/

Summarize the videos that you watch and discuss the applied concepts in the following terms:

• Pair one fundamental concept from Newtons law of motion(first, second or third) or in text with the video (e.g., speed, velocity, force, gravity, projectile motion, work, power, energy transfer etc.).
• Describe the relationship between the concept described in text (images below) and video(s)

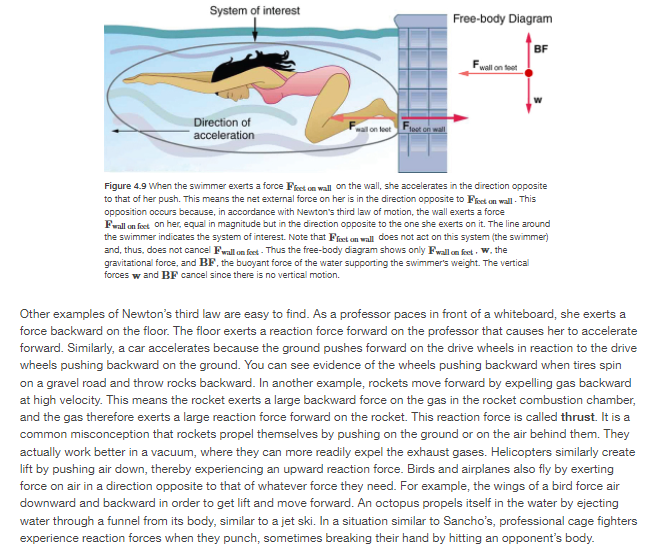
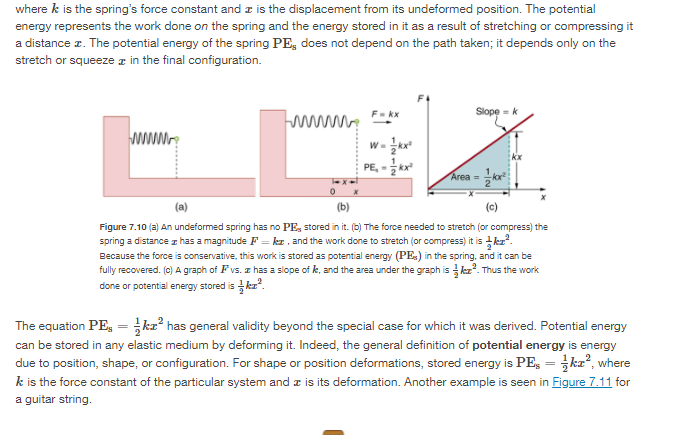
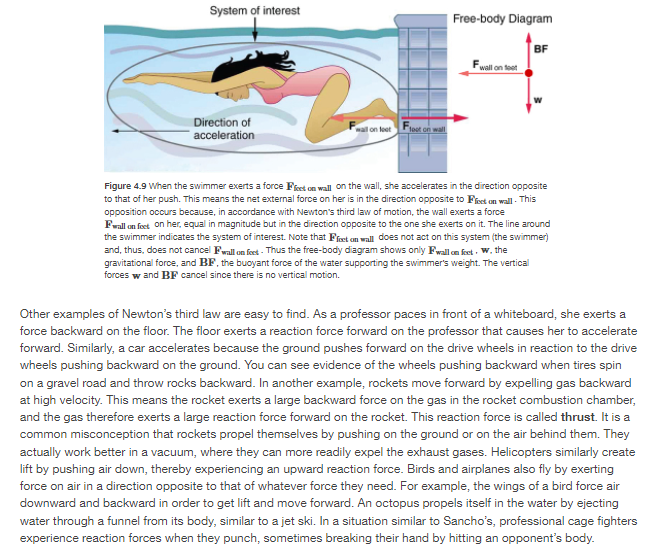
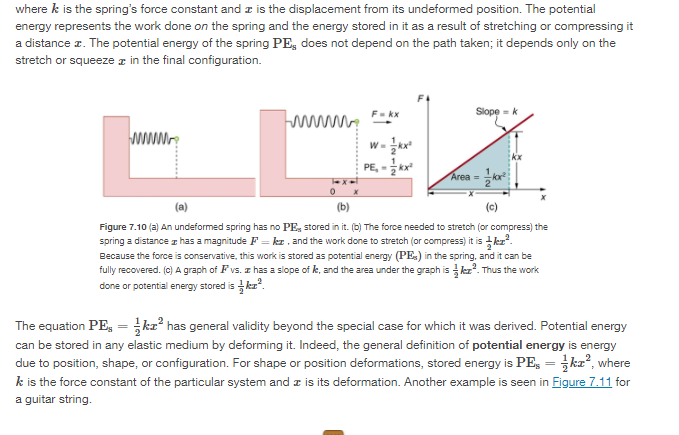
Experience suggests that an object at rest will remain at rest if left alone, and that an object in motion tends to slow down and stop unlllo some effort is made to keep it moving. What Newton's rst law of motion states, however, is the following: HEWTON'S FIRST LAW OF MOTION A body at rest remains at rest, or, if in motion, remains in motion at a constant velocity unless acted on by a net enemal force. Note the repeated use of the verb "remains." We can think of this law as preserving the status quo of motion. Flather than contradicting our experience, Newton's rst law of motion states that there must be a cause {which is a net external force] for there to be any change fn velocfty feithera change in magnitude or direcoril'. We will dene net external force in the next section. An object sliding across a table or oor slows down due to the net force of friction acting on the object; If friction disappeared, would the object still slow down? The idea of cause and effect is cmcial in accurately describing what happens in various situations. For example, consider what happens to an object sliding along a rough horizontal surface. The object quickly grinds to a halt. If we spray the surface with talcum powder to make the surface smoother, the object slides farther. If we make the surface even smoother by rubbing lubricating oil on it, the object slides farther yet. Extrapolating to a frictionless surface, we can imagine the object sliding in a straight line indenitely. Friction is thus the cause of the slowing {consistent with Newton's first law}. The object would not slow down at all if friction were completely eliminated. Consider an air hockey table. When the air is turned off, the puck slides only a short distance before friction slows it to a stop. However, when the air is turned onI it creates a heady frictionlI-Ic surface, and the puck glides long distances without slowing down. Additionally, if we know enough about the friction, we can accurately predict how quickly the object will slow down. Friction is an extemal force. Newton's first law is completely general and can be applied to anything from an object sliding on a table to a satellite in orbit to blood pumped from the heart. Experiments have ti'ioroughly veried that any change in velocity {speed or direction} must be caused by an external force. The idea of generally applicable orunfversal laws is important not only hereit is a basic feature of all laws of physics. Identifying these laws is like recognizing patterns in nature from which further patterns can be discovered. The genius of Galileo, who rst developed the idea for the rst law, and Newton, who clarified it, was to ask the fundamental question, \"What is the cause?" Thinking in terms of cause and effect is a worldview fundamentally different from the typical ancient Greek approach when questions such as "Why does a tiger have stripes?\" would have been answered in Aristotelian fashion, \"That is the nature of the beast' True perhaps, but not a useful insight. Mass The property of a body to remain at rest or to remain in motion with constant velocity is called inerlia. Newton's rst law is often called the law of inertia. As we know from experience, some objects have more inertia than others. ft is obviously more difficult to change the motion of a large boulder than that of a basketball, for example. The inertia of an object is measured by its mass. Floughly spealdng, mass is a measure of the amount of \"stuff" [or matter] in something. The quantity or amount of matter in an object is determined by the numbers of atoms and molecules of various types it contains. Unlike weight, mass does not vary with location. The mass of an object is the same on Earth, in orbit, or on the surface of the Moon. In practice, it is very difcult to count and identify all of the atoms and molecules in an object; so masses are not often determined in this manner. Operationally, the masses of objects are determined by oompason with the standard kilo-gram. \fNow, it seems reasonable that acceleration should be directly proportional to and in the same direction as the net {total} external force acting on a system. This assumption has been yerified experimentally and is illustrated in Egu'e 4.5. In part {a}, a smaller force causes a smaller acceleration than the larger force illustrated in part {c}. For completenI-Io, the vertical forces are also shown; they are assumed to cancel sinoe there is no acceleration in the vertical direction. The 1.Itertical forces are the weight W and the support of the ground N, and the horizontal force 1' represents the force of friction. These will be discussed in more detail in later sections. For now, we will clefine friction as a force that opposes the motion past each other of objects that are touching. gure 4.5M shows how vectors representing the external forces add together to produce a net force, Fug. To obtain an equation for Newton's second law, we rst write the relationship of acceleration and net external force as the proportionality m... where the symbol or means "proportional to," and PM is the net external force. {The net external force is the vector sum of all external forces and can be determined graphically, using the head-totail method, or analytically, using components. The techniques are the same as for the addition of other yectors, and are coyered in E Dimensional Kinematics.) This proportionality states what we have said in wordsacceleration is directly pmporonal' to the net external force. Once the system of interest is chosen, it is important to identify the external forces and ignore the intemal ones. It a tremendous simplication not to have to consider the numerous internal forces acting between objects within the system, such as muscular forces within the child's body, let alone the myriad of forces between atoms in the objects, but by doing so, we can easily solve some very complex problems with only minimal encr due to our simplication Now, it also seems reasonable that acceleration should be inyersely proportional to the mass of the system. In other words, the larger the mass [the inertia), the smaller the acceleration prcduoed by a given foroe. And indeed, as illustrated in gure 4.5, the same net external force applied to a car produces a much smaller acceleration than when applied to a basketball. The proportionality is written as 1 not; where m is the mass of the system. Expeliments have shown that acceleration is exactly inyersely proportional to mass, just as it is exactly linearfy proportional to the net external force. unwary-mammogram F F It'll Figure 4.6 The same force exerted on systems ofdilferent massa pristine-s Izltfererrt accelaatiens. [ajuA basketball player pushE on a basketball to mat-re a pass. [the effect of gravity onthe ball is ignored] jbj 111a same player exerts an identical force on. a stalled SLI'u' and prodlnes a tar-smaller aoeeleration {even iffrietion is negligible}. te]'l1'uefree-body diagrams are identical. permitting direct comparison ofthe two situations. A series of patterns forti'uefree-bolzl}.I diagram will emerge as you do more problems. It has been found 1at 1e acceleration of an object depends only on the net extemal force and the mass of line object. l[Zombining the two proportionalities just given yields Newton's second law of motion. NEWTDN'S SEGDND LAW DF MOTION The acceleration of a system is directly proportional to and in line same direction as the net external force acng on the system, and inversely proportional to its mass. In equation form, Newton's second law of motion is F\" I a = . ,,, a This is often written in the more familiar form Fm=m1L When only the magnilllde of foree and acceleration are considered, 1is equation is simply Fm =ma. Although these last two equaons are really the same, the rst gives more insight into what Newton's second law means. The law is a cause and effect relationship among three quantities that is not simply based on their definitions. The validity of the second law is completely based on experimental verication. Units of Force Fm = ma is used to dene the units of force in terms of the three basic units for mass, length, and lime. The SI unit of force is called the newton [abbreviated N} and is the force needed to accelerate a 'lkg system at the rate of 11:1,! 5\". That is, since Fm = ma, 1 N = 1 kg . mfg\". While almost the entire world uses the newton for line unit of force, in the United States 'le most familiar unit of force is the pound [lb], where 'l N = [1225 lb. Weight and the Gravitational Force When an object is dropped, it aocelerates toward the center of Earth. Newton's second law states that a net force on an object is responsible for its acceleraijon. If air resistance is negligible, 1e net force on a falling object is the gravitational force, commonly called its weight if. I|.I'|.Ileight can be denoted as a vector W because it has a direction; down isI by definition, the direction of gravity, and hence weight is a downward force. The magnilllde of weight is denoted as w. Galileo was instrumental in showing that, in the absence of air resistanoe, all objects fall with the same acceleration 3. Using IGalileo's result and Newton's second law, we can derive an equation for weight. lEonsider an object with mass :1: Falling downward toward Earth. It experiences only the downward force of gravity, which has magnitude in. Newton's second law states that the magnitude of the net extemal force on an object is Fm; = me Since the object experiences only the downward force of gravity, Fm = m. We know that the acceleration of an object due to gravity is g, or a. = g. Substituting these into Newton's second law gives IWEI'IEH T This is the equation for weightthe gravitational force on a mass m: w=mg. Since 9 = 9.30 1113's2 on Earth, the weight of a 1.0 kg object on Earth is 9.3 N, as we see: to = my ={1o kg]{9.8[i mfg\"): as N. Ftecall that y can take a positive or negative value, depending on the positive diection in the coordinate system. Ele sure to take this into consideration when solving problems with weight. When the net extemal force on an object is its weight, we say that it is in freefall. That is, the only force acting on the object is the force of gravity. In the real world, when objects fall downward toward Earth, they are never ti1.|ly in free-fall because there is always some upward force from the air acting on the object. The acceleration due to gravity 9' varies slightly over the su'Face of Earth, so that the weight of an object depends on location and is not an intrinsic property of the object. Weight varies dramatically if one leaves Earth's surface. On the Moon, for example, the acceleration due to gravity is only 1.25 mfsa. A till-kg rnass thus has a weight of 9.8 N on Earth and only about 1.? N on the Moon. The broadest definition of weight in this sense is that the weight ofan object is the gravitaonal' force on it from the nearest .iarge body, such as Earth, the Moon, the Sun, and so on. This is the most common and useful denition of weight in physics. lt diers dramatically, however, from the denition of weight used by NASA and the popular media in relation to space travel and exploration. When they speak of \"weightlessness\" and \"microgravity," they are really reterri rig to the phenomenon we call \"tree-fall" in physics. We shall use the above denition of weight, and we will make careFul distinctions between treetall and actual weightlessness. It is important to be aware that weight and mass are very dil'Ferent physical quantities, although they are closely related. Mass is the quantity of matter {how much \"stu'? and does not vary in classical physics, wl'Iereas weight is the gravitational force and does vary depending on gravity. it is ternpting to equate the two, since rmst of our examples take place on Earth, where the weight of an object only varies a little with the location of the object. Furthermore, the terms mass and weight are used interchangeably in everyday language; for example, our medical records often show our "weight" in kilograms, but never in the correct un its of newtons. Elaseball relief pitcher Mariano Fliyera was so highly regarded that during his retirement year, opposing teams conducted farewell presentations when he played at their stadiums. The Minnesota Twins offered a unique gift: A chair made of broken bats. Any pitch can break a bat, but with Hiyera's signature pitchknown as a cutterthe ball and the bat frequently came together at a point that shattered the hardwood. Typically, we think of a baseball or softball hitter exerting a force on the incoming ball, and baseball analysts now focus on the resulting "exit velocity" as a key statistic. Elut the force of the ball can do its own damage. This is exactly what happens whenever one body exerts a force on anotherthe rst also experiences a force {equal in magnitude and opposite in direction). Numerous common experiences, such as stiibbing a toe or pushing off the floor during a jump, conrm this. It is precisely stated in Newton's third law of motion. HEWTDN'S THIFID LAW DF HDTIUN I|Il'r'l'leneirer one body exerts a force on a second body, the fist body experiences aforce that is equal in magnitude and opposite in direction to the force that it exerts This law represents a certain symmetryin nature: Forces always occur in pairs, and one body cannot exert a force on another without experiencing a force itself. We sometimes refer to this law loosely as n'acticnreaction,\" where the force exerted is the action and the force experienced as a consequence the reaction. Newton's third law has practical uses in analyzing the origin of forces and understanding which forces are external to a system. We can readily see Newton's third law at work by taking a look at how people move about Consider a swimmer pushing off from the side of a pool, as illustrated in gure 4.9. She pushes against the pool wall with her feet and accelerates in the direction opposite to that of her push. The wall has exerted an equal and opposite force back on the swimmer. You might think that two equal and opposite forces would cancel, but they do not because they act on different system. In this case, there are two systems that we could inyestigate: the swimmer or the wall. If we select the swimmer to be the system of interest, as in the gure, then Fun mm: is an external force on this system and affects its motion. The swimmer moves in the direction of Fun\" [53. In contrast, the force PM\\fNormal Force Weight {also called foree of gravity] is a pervasive force that acts at all times and must be counteracted to keep an object from falling. You definitely notice that you must support the weight of a heavy object by pushing up on it when you hold it stationary, as illustrated in gure 4-12'l3ll- But how do inanimate objects like a table support the weight of a mass placed on them, such as shown in gu'e 4-12'lbl'? When the bag of dog food is placed on the table, the table actually sags slightly under the load. This would be noticeable if the load were placed on a card talole, but even rigid objects deform when a force is applied to them. Unless the object is deformed beyond its limit, it will exert a restoring foroe much like a deformed spring {or trampoline or diving board]. The greater the deformation, the greater the restoring force. So when the load is placed on the table, the table sags until the restoring foree becomes as large as the weight of the load. At this point the net external force on the load is zero. That is the situation when the load is stationary on the table. The table sags quickly, and the sag is slight so we do not notice it. Elut it is similar to the sagging of a trampoline when you climb onto it. {hi ls l- I j. Flu-mm Figure 4.12 (at The person hold'ng the bag ofdog food must supply an upward force Fh-i equal 'ru mag'uitude and opposite 'l'u Izlrection bathe neig'rt ofthe food 1r. jbj'l'l'teoardtahle sags M'renthe dog food is placed on it. much lil-re astiff trampoline. Elastic restoring force in. the table you as it sags mtjl they supplyaforoe N equal in magnitude and opposite in direction to the wag-it of the load. We must conclude that whatever supports a loadI be it animate or not, must supply an upward foree equal to the weight of the loadI as we assumed in a few of the previous examples. If the force supporting a load perpendicular to the surface of contact between the load and its support1 this force is defined to be a normal force and here is given the symbol N. (This is not the unit for force N.) The 1.r.r-I:Iurd normal means perpendicular to a surface. The normal force can be less than the object's weight if the object is on an incline, as you will see in the next example. Tension A tension is a force along the length of a medium, especially a force canted by a exible medium, such as a rope or cable. The word \"tension\" comes from a Latin word meaning "to stretch.\" Not coincidentally, the flexible cords that cany muscle forces to other parts of the body are called tendons. Any flexible connector, such as a sting, rope, chain, wire, or cable, can exert pulls only parallel to its length; thus, a force canted by a exible connector is a tension with direction parallel to the connector. It is important to understand that tension is a pull in a connector. In contrast, consider the phrase: \"You can't push a rope." The tension force pulls outward along the two ends of a rope. Consider a person holding a mass on a rope as shown in gure 4.15. T lo-m \"-1 'I' I' I Figure 4.15 when. a perfectly exible omneo'bor [one requiring no force to bend it] such asthis rope transrri'ts a force T. thatforoe must be parallel to the length. ofthe rope. as shown. The pull smelt. a exible connector exerts is atension. Note that the rope pulls with equal force but in opposite directions onthe hand and the moot-ted rrass [neglect'ng the weigtt ofthe rope]. This is an example of Newton'sth'rd law. the rope is the medu'n that carries the equal and opposite forces bonuses theme objects. The tension where in therope between the hand and the mass is qual. Once you have determined the tension in one lowion. you heme deterrrined thetension at all lctanE along the rope. Tension in the rope must equal the weight of the supported mass, as we can prove using Newton's second law. If the EDDkg mass in the figure is stationary, then its acceleration is zero, and thus PM = D. The only external forces acting on the mass are its weight W and the tension T supplied by the rope. Thus, Fm=Tw=t], where T and 'tI'J' are the magnitudes of the tension and weight and their signs indicate direction, with up being positive here. Thus, just as you would expect, the tension equals the weight of the supported mass: T=w =rng. 4.42 Work Done Against Gravity Climbing stairs and lifting objects is work in both the scientific and everyday senseit is work done against the gravitational force. When there is work, there is a transformation of energy. The work done against the gravitational force goes into an important form of stored energy that we will explore in this section. Let us calculate the work done in lifting an object of mass 111 through a height h, such as in gure 15. If the object is lifted straight up at constant speed, then the force needed to lift it is equal to its weight mg. The work done on the mass is then W : Fd : mgh. We define this to be the gravitational potential energy [FEE] put into (or gained by) the objectEarth system. This energy is associated with the state of separation between two objects that attract each other by the gravitational force. For convenience. we refer to this as the P133 gained by the object, recognizing that this is energy stored in the gravitational eld of Earth. Why do we use the word \"system\"? Potential energy is a property of a system rather than of a single objectdue to its physical position. An object's gravitational potential is due to its position relative to the surroundings within the Earthobject system. The force applied to the object is an external force, from outside the system. When it does positive work it increases the gravitational potential energy of the system. Because gravitational potential energy depends on relative position, we need a reference level at which to set the potential energy equal to 0. We usually choose this point to be Earth's surface, but this point is arbitrary; what is important is the difference in gravitational potential energy, because this difference is what relates to the work done. The difference in gravitational potential energy of an object [in the Earthobject system} between two rungs of a ladder will be the same for the rst two rungs as for the last two rungs. Converting Between Potential Energy and Kinetic Energy Gravitational potential energy may be converted to other forms of energyI such as kinetic energy. If we release the mass, gravitational force will do an amount of work equal to High on it, thereby increasing 'rts kinetic energy by that same amount {by the work-energy theorem}. We will find it more useful to oonsider just the conversion of PBS to HE without explicitiy considering the intermediate step of work. {See mm.) This shortcut makes it is easier to solve problems using energy {if possible] rather than explicitly using forces. F l 1:1"...le ' 0 till lb] Figue 15 ta]'l1'ue work doneto lift theweig'tt is shared in the mass-Earth system as gravitational pots-mat evergy. [to] As the \"reign moves downward. this gravitational potential energy is tiansfen'edto tt'vecud-coo dock. cl) Ililll-IIHIIl-III =man More precisely, we dene the change in gravitational potential energy ME! to be lilo-EE = wk, 12? where, for simplicity, we denote the change in height by 31 rather than the usual h. Note that h is positive when the final height is greater than the initial height, and vice versa. For example, if a DEEDkg mass hung from a cuckoo clock is raised 1.1][1 m, then its change in gravitational potential energy is High {sans kg} (9.30 mfsg) {1.011 m) T28 4.90 kg . mfsg= 4.9:} J. Note that the units of gravitational potentiaJ energy turn out to be joulesI the same as for work and other forms of energy. As the clock runs, the mass is lowered. We can think of the mass as gradually giving up its 4.9] J of gravitational potential energy, without directly considering the force of gravity that does the work. Potential Energy and Conservative Forces Work is done by a force, and some forces, such as weight, have special characteristics. A conservative force is one, like the gravitational force, for which work done by or against it depends only on the starting and ending points of a motion and not on the path taken. We can define a potential energy {PE} for any conservative force, just as we did for the gravitational force. For example, when you wind up a toy, an egg timer, or an oldfashioned watch, you do work against its spring and store energy in it. We treat these springs as ideal, in that we assume there is no friction and no production of thermal energy.) This stored energy is recoverable as work, and it is useful to think of it as potential energy contained in the spring. Indeed, the reason that the spring has this characteristic is that its force is conservative. That is, a consenatiye force results in stored or potential energy. Gravitational potential energy is one example, as is the energy stored in a spring. We will also see I'rctw conservative forces are related to the conservation of energy. PDTEHTIAL ENERGY AND CONSERVATIVE FORCES Potential energy is the energy a system has due to position, shape, or congu'ation. It is stored energy that is completely recoverable. A conservative force is one for which work done by or against it depends only on the starting and ending points of a motion and not on the path taken. We can dene a potential energy (PE) for any conservative force. The work done against a conservative force to reach a final conguration depends on the conguration, not the path followed, and is the potential energy added. Potential Energy of a Spring First, let us obtain an expression for the potential energy stored in a spring {FEE}. We calculate the work done to stretch or compress a spring that obeys Hooke's law. [Hooke's law was examined in Elasticity: Stress and Strain, and states that the magnitude of force F on the spring and the resulting deformation L are proportional, F = kLJ [See gure 1111} For our spring, we will replace AL {the amount of deformation produced by a force F] by the distance :I: that the spring is stretched or compressed along its length. So the force needed to stIetch the spring has magnitude F = For, where l: is the spring's force constant. The force increases line-arty from t] at the start to k: in the fully stretched pos'rtion. The average force is he\". Thus the work done in stIetching or compressing the spring is 1W; = F}! = [%] a: = lezg' Alternatiyely, we noted in Kinetic Energy and the Work- Eiergy Theorem that the area under a graph of F vs. :1: is the work done by the force. In g ure ?.1'Dl[c} we see that this area is also %k12 . We therefore define the potential energy of a spring, FEE, to he 1 PE:a = Eh\where k is the spring's force constant and c is the displacement from its undeformed position. The potential energy represents the work done on the spring and the energy stored in it as a result of stretching or compressing it a distance c. The potential energy of the spring PE, does not depend on the path taken; it depends only on the stretch or squeeze x in the final configuration. F F.kx Slope = k -kx KX PEG Area = (a) (b) (c) Figure 7.10 (a) An undeformed spring has no PE, stored in it. (b) The force needed to stretch (or compress) the spring a distance x has a magnitude F = kx , and the work done to stretch (or compress] it is 1 kx'. Because the force is conservative. this work is stored as potential energy (I'Es) in the spring, and it can be fully recovered. (c) A graph of Ivs. I has a slope of k, and the area under the graph is = ker?. Thus the work done or potential energy stored is _ kx". The equation PE, = = kx has general validity beyond the special case for which it was derived. Potential energy can be stored in any elastic medium by deforming it. Indeed, the general definition of potential energy is energy due to position, shape, or configuration. For shape or position deformations, stored energy is PE, = = kx , where k is the force constant of the particular system and I is its deformation. Another example is seen in Figure 7.11 for a guitar string.Conservation of Mechanical Energy Let us now consider what form the work-energy theorem takes when only conservative forces are involved. This will lead us to the conservation of energy principle. The workenergy theorem states that the net work done by all forces acting on a system equals its change in kinetic energy. In equation form, this is 1 1 W =mu\"m \"=aKE. m n" 2 2 1'1] - If only conservative forces act, then Wm = Wu, 144 where W: is the total mrk done by all conservative forces. Thus, WE = lm. 145 Now, if the conservative force, such as the gravitational force or a spring force, does work, the system loses potential energy. That is, \"'1 = PE. Therefore, .r'_'l.PE = ME I" 45 or KE + PE = 'l]. 14? This equation means that the total kinetic and potential energy is constant for any process involving only conservative forces. That is, KE + PE = constant or [conservative forces only}, 148 KEi+PEi=KEI+PEf I.vhere i and f denote initial and final values. This equation is a form of the work-energy theorem for conservative forces; it is known as the conservation of mechanical energy plinciple. Flernember that this applies to the extent that all the forces are conservative, so that friction is negligible. The total kinetic plus potential energy of a system is dened to be its mechanical energy, {HE + PE]. In a system that experiences only conservative forces, there is a potential energy associated with each force, and the energy only changes forrn between KB and the various types of PE, with the total energy remaining constant. How the Work-Energy Theorem Applies Now let us consider what form the workenergy theorem takes when both conservative and nonoonservative forces act. We will see that the work done by nonconservative foroes equals the change in the mechanical energy of a system. As noted in Kinetic Energy and the I|.I'|.Ilork-Energy Theorem the workenergy theorem states that the net work on a system equals the change in its kinetic energy, or Wm = KE. The net work is the sum of the work by no nconservative forces plus the work by conservative forces. That is, Woof = Wm + Win 155 so that Wm + W: = 5.35:, 155 where Wm is the total work done by all nonconservative forces and We is the total work done by all conservative forces. Figure 116 .5. person pushes a crate up a ramp. do'ng work onthe crate. Friction and gravitational force [not shown} also do work onthe crate: both forces oppose the person's push. its the mate is pushed up the lamp, i'tga'rrs mechanical energy. imply'rrg that the workdone bythe person is greater than the work done by friction. Consider gure T315, in which a person pushes a crate up a ramp and is opposed by friction. As in the previous section, we note that work done by a conservative force comes from a loss of gravitational potential energy, so that We = PE. Substituting this equation into the previous one and solving for Wu gives Wm = aKE + sea. 15? This equation means that the total mechanical energy {HE + PE] changes by exactly the amount of work done by nonconservative forces. In gure 115, this is the work done by the person min us the work done by friction. So even if energy is not conserved for the system of interest {such as the crate}, we know that an equal amount of work was done to cause the change in total mechanical energy. We rearrange Wm = AKE + PE to obtain KEi+PEi+W =KEf+PEL 155 This means that the amo unt of work done by nonconservative forces adds to the mechanical energy of a system. If Wm is positive, then mechanical energy is increased, such as when the person pushes the crate up the ramp in gure 115. If Wm is negative, then mechanical energy is decreased, such as when the rock hits the ground in gure 11 bib}. lf WE is zero, then mechanical energy is conserved, and nonco nser'vative forces are balanced. For example, when you push a lawn mower at constant speed on level groundI your work done is removed by the work of friction, and the mower has a constant energy. Law of Conservation of Energy Energy, as we have noted, is conseryed, making it one of the most important physical quantities in nature. The law of conservation of energy can be stated as follows: Total energyr is constant in anyr process. It may change in form orbe transferred from one system to another, but the total' remains the same. We have explored some forms of energy and some ways it can be transferred from one system to another. This exploration led to the definition of two major types of energymechanical energy [KE + PE} and energy transferred via work done by nonconseryatjye forces (Wm). But energy takes many other forms, manifesting itself in many different ways, and we need to be able to deal with all of these before we can write an equation for the aboye general statement of the conservation of energy. l[Cl'ther Fom1s of Energy than Mechanical Energy At this point, we deal with all other forms of energy by lumping them into a single group called other energy {OE}. Then we can state the conservation of energy in equation form as KEi + PEi + Wm + 0E1 = KE: + PEf + GEE. Il' All types of energy and 1rlrork can be included in this yery general statement of consenration of energy. Kinetic energy is KE, work done by a conseryatiye force is represented by PE, work done by nonconseryatiye forces is Wm, and all other energies are included as DE. This equation applies to all previous examples; in those situations DE was constant, and so it subtracted out and was not directly considered. MAKING GDHHEGTIDHS: USEFULHESS OF THE ENERGY GDHSEHVATION PHIHGIP LE The fact that energy is conserved and has many forms makes it very important. You will nd that energy is discussed in many contexts, because it is involved in all processes. it will also become apparent that many situations are best understood in terms of energy and that problems are often most easily conceptualized and sohred by considering energy. lI.I'I.I'hen does DE play a role? One example occu's when a person eats. Food is oxidized with the release of carbon dioxide, water, and energy. Some of this chemical energy oonyerted to kinetic energy when the person mouse, to potential energy when the person changes altitude, and to thermal energy {another form of DE]. Some of the Many Foms of Energy |I.I'I.I'hat are some other forms of energy? You can probably name a number of forms of energy not yet discussed. Many of these will be covered in later chapters, but let us detail a few here. Electrical energy is a common form that is converted to many other forms and does work in a wide range of practical situations. FuelsI such as gasoline and food, carry chemical energy that can be transten'ed to a system through oxidation. Chemical fuel can also produce electrical energy, such as in batteries. Batteries can in turn produce light, which is a very pure form of energy. l'v'lost energy sources on Earth are in fact stored energy from the energy we receive from the Sun. We sometimes refer to this as radiant energy, or electromagnetic radiation, which includes visible light, infrared, and ultraviolet radiation. Nuclear energy comes from processes that convert measurable amounts of mass into energy. Nuclear energy is transformed into the energy of sunlight, into electrical energy in power plants, and into the energy of the heat transfer and blast in weapons. Atoms and molecules inside all objects are in random motion. This internal mechanical energy from the random motions is called ihennal energy, because it is related to the temperature of the object. These and all other forms of energy can be converted into one another and can do work. Table T.1 gives the amount of energy stored, used, or released from various objects and in various phenomena. The range of energies and the variety of types and situations is impressive. Transformation of Energy The transformation of energy from one form into others is happening all the time. The chemical energy in food is converted into thermal energy through metabolism; light energy is converted into chemical energy through photosynthesis. In a Ialger example, the chemical energy contained in coal is converted into thermal energy as it burns to turn water into steam in a boiler. This thermal energy in the steam in turn is converted to mechanical energy as it spins a turbine, which is connected to a generator to produce electrical energy. {In all of these examples, not all of the initial energy is converted into the forms mentioned. This important point is discussed later in this section.) Another example of energy conversion occurs in a solar cell. Sunlight impinging on a solar cell {see gure FED! produces electIicity, which in turn can be used to n.|n an electric motor. Energy is converted from the primary source of solar energy into electrical energy and then into mechanical energy. Figure 1.21] Solar energy is converted into electrical energy bysotar oetls. which is used to rum 3 motor in this solar-porreralrciatt tu'edit: NASH