Water is flowing in a channel at a rate of Q = 30 m/s. The critical depth x for such a

channel must satisfy the equation

0=1-BQ2gA3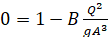 Eq. 1

where g = 9.81 m/s, A = the cross sectional area (m), and B = the width of the

channel at the surface (m). For this case, the width and the cross-sectional area can be

related to depth x by:

B=3+x and A=3x+x22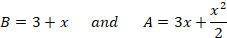

Solve for the critical depth using (a) Bisection with the initial guesses of xl = 1.0 and

xu = 3, (b) False position with the initial guesses of xl = 1.0 and xu = 3. Iterate until the approximate error falls below 10%.