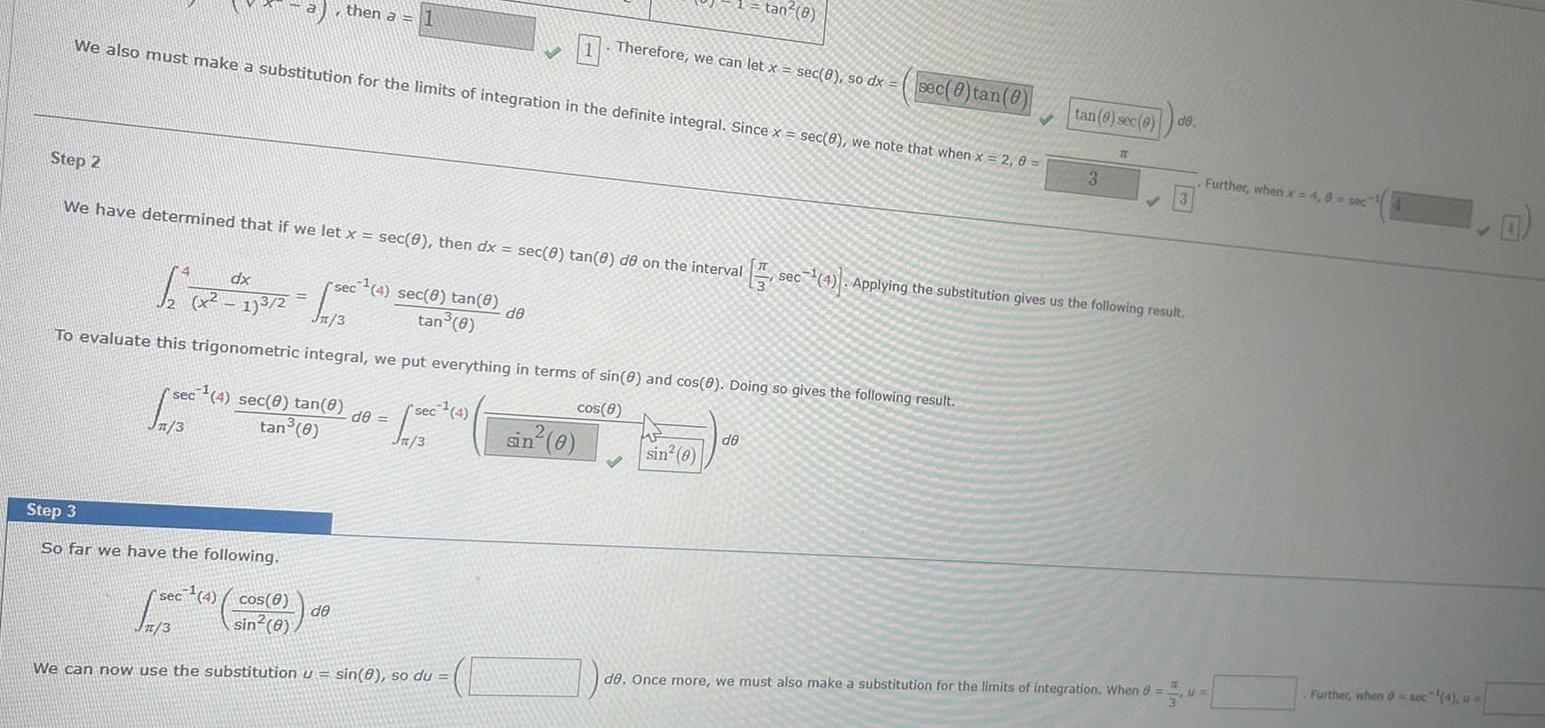
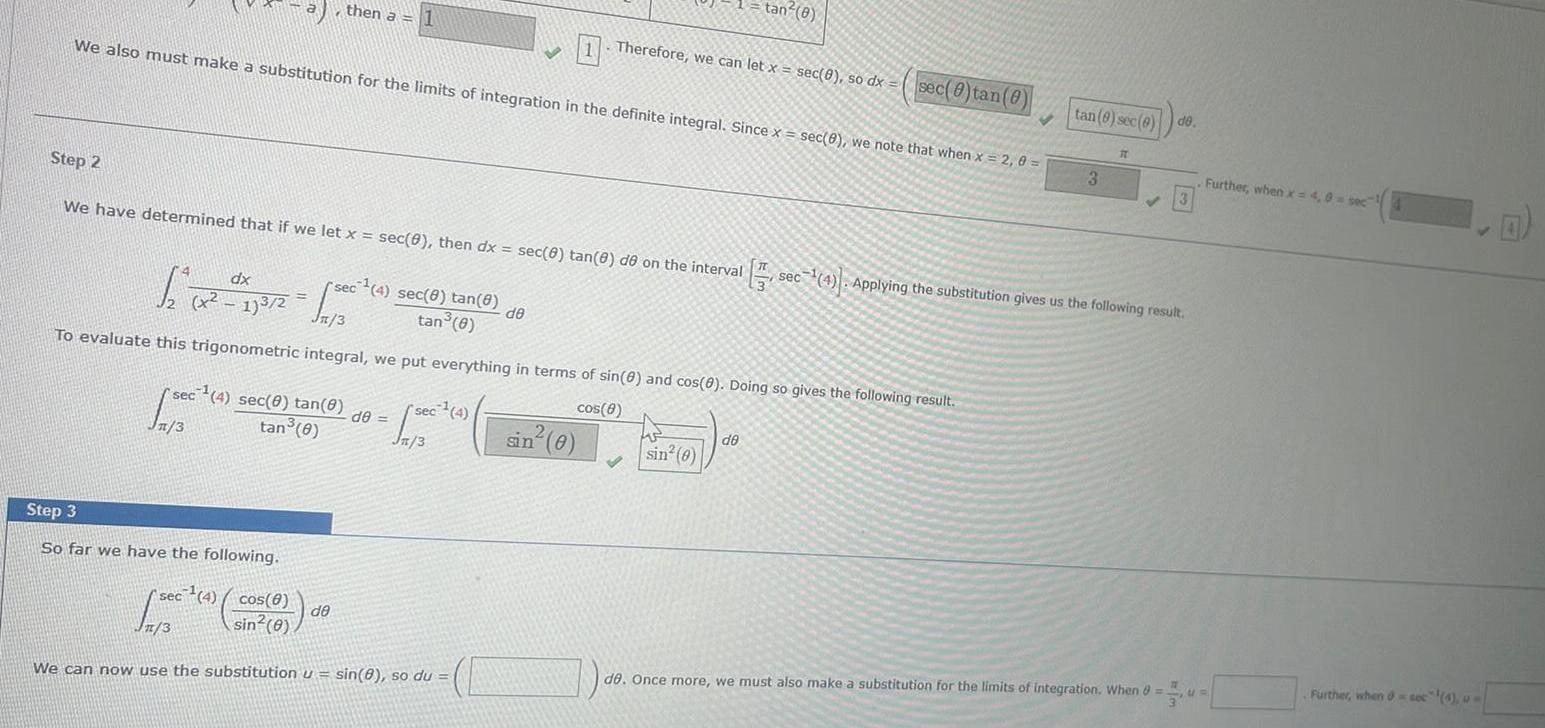
We also must make a substitution for the limits of integration in the definite integral Since x sec 8 we note that when x 2 0 then a 1 Step 2 We have determined that if we let x sec 0 then dx sec 8 tan 8 de on the interval sec 4 sec 0 tan 0 1 3 tan 0 Step 3 So far we have the following rsec 4 sec 8 tan 8 tan 0 dx 1 x x 173 2 1500 Jn 3 To evaluate this trigonometric integral we put everything in terms of sin 8 and cos 0 Doing so gives the following result cos 8 de de sec 4 Jn 3 sec 4 cos 8 Jn 3 sin 0 We can now use the substitution u sin 8 so du de Therefore we can let x sec 0 so dx sin 0 tan 8 V sin 0 de sec 0 tan 0 tan 6 sec 0 de 3 IT 3 sec 4 Applying the substitution gives us the following result de Once more we must also make a substitution for the limits of integration When 8 CI Further when x 4 8 sec Further when soc 4 u