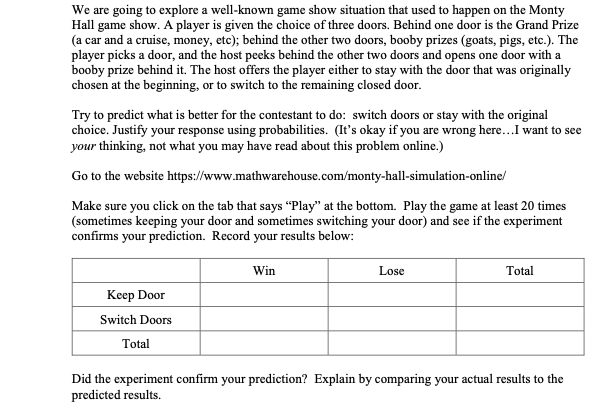
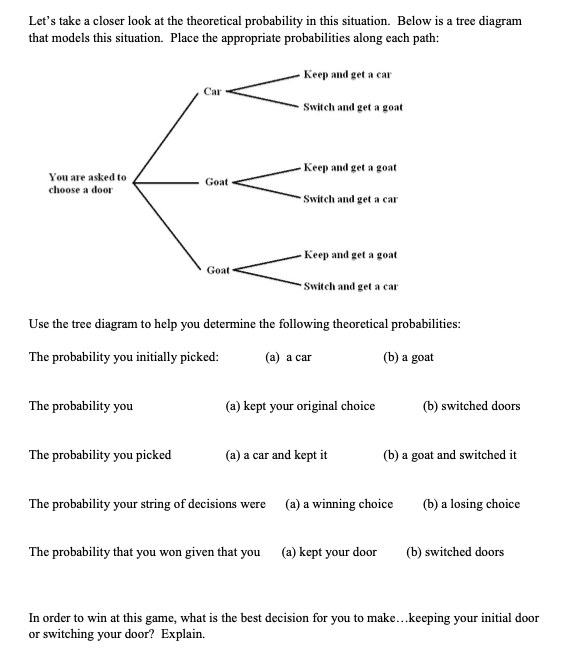
We are going to explore a well-known game show situation that used to happen on the Monty Hall game show. A player is given the choice of three doors. Behind one door is the Grand Prize (a car and a cruise, money, etc); behind the other two doors, booby prizes (goats, pigs, etc.). The player picks a door, and the host peeks behind the other two doors and opens one door with a booby prize behind it. The host offers the player either to stay with the door that was originally chosen at the beginning, or to switch to the remaining closed door. Try to predict what is better for the contestant to do: switch doors or stay with the original choice. Justify your response using probabilities. (It's okay if you are wrong here...I want to see your thinking, not what you may have read about this problem online.) Go to the website https://www.mathwarehouse.com/monty-hall-simulation-online/ Make sure you click on the tab that says "Play" at the bottom. Play the game at least 20 times (sometimes keeping your door and sometimes switching your door) and see if the experiment confirms your prediction. Record your results below: Keep Door Switch Doors Total Win Lose Total Did the experiment confirm your prediction? Explain by comparing your actual results to the predicted results. Let's see how the law of large numbers comes into play... As the number of trials increases, the experimental probability should approach Click on the tab that says "Simulate" and add to your results. (For simulations of 100 or less, you can use the speed "fast" to watch the game unfold, but if you select 500 or 1000, use "instant") Be sure that sometimes you simulate keeping the door, and sometimes simulate switching doors. Record your results again below: Keep Door Switch Doors Total Win Lose Based on these results, if you keep your door, what is the probability of winning? Total Make a prediction about what the theoretical probability of winning would be if you keep your door. Based on these results, if you switch doors, what is the probability of winning? Make a prediction about what the theoretical probability of winning would be if you switch your door. Do any of the probabilities (Keep + Win, Keep + Lose, Switch + Win, Switch + Lose) have a similar value? Which ones? Why would that make sense? Let's take a closer look at the theoretical probability in this situation. Below is a tree diagram that models this situation. Place the appropriate probabilities along each path: Keep and get a car Car Switch and get a goat Keep and get a goat You are asked to choose a door Goat Switch and get a car Keep and get a goat Goat - Switch and get a car Use the tree diagram to help you determine the following theoretical probabilities: The probability you initially picked: (a) a car (b) a goat The probability you (a) kept your original choice (b) switched doors The probability you picked (a) a car and kept it (b) a goat and switched it The probability your string of decisions were (a) a winning choice (b) a losing choice The probability that you won given that y you (a) kept your door (b) switched doors In order to win at this game, what is the best decision for you to make...keeping your initial door or switching your door? Explain. Wrap-Up: What happened here? When you initially choose your door, you have a 1/3 chance you selected the car and a 2/3 chance the car is behind the other doors. Once an incorrect choice is revealed, the chance of you initially picking the car hasn't changed. Instead, all the probability associated to the car being behind the other doors shifts to the only remaining alternative door. Let's think about it this way...If there were 100 doors, you would only have a 1/100 chance of selecting right initially. If I then opened 98 wrong doors, it is more likely that you initially selected right, or more likely that the prize is behind the one remaining door? Then same logic works when reduced down to 3 options instead of 100. The Three Prisoners problem appeared in Martin Gardner's Mathematical Games column in Scientific American in 1959. He put it like this: Three men - A, B and C - were in separate cells under sentence of death when the governor decided to pardon one of them. He wrote their names on three slips of paper, shook the slips in a hat, drew out one of them and telephoned the warden, requesting that the name of the lucky man be kept secret for several days. Rumor of this reached prisoner A. When the warden made his morning rounds, A tried to persuade the warden to tell him who had been pardoned. The warden refused. "Then tell me,' said A, 'the name of one of the others who will be executed. If B is to be pardoned, give me C's name. If C is to be pardoned, give me B's name. And if I'm to be pardoned, flip a coin to decide whether to name B or C.' 'But if you see me flip the coin,' replied the wary warden, 'you'll know that you're the one pardoned. And if you see that I don't flip a coin, you'll know it's either you or the person I don't name.' 'Then don't tell me now," said A. "Tell me tomorrow morning." The warden, who knew nothing about probability theory, thought it over that night and decided that if he followed the procedure suggested by A, it would give A no help whatever in estimating his survival chances. So next morning he told A that B was going to be executed. After the warden left, A smiled to himself at the warden's stupidity. There were now only two equally probable elements in what mathematicians like to call the 'sample space' of the problem. Either C would be pardoned or himself, so by all the laws of conditional probability, his chances of survival had gone up from 1/3 to ... Did A reason correctly? What are A's chances of being pardoned?