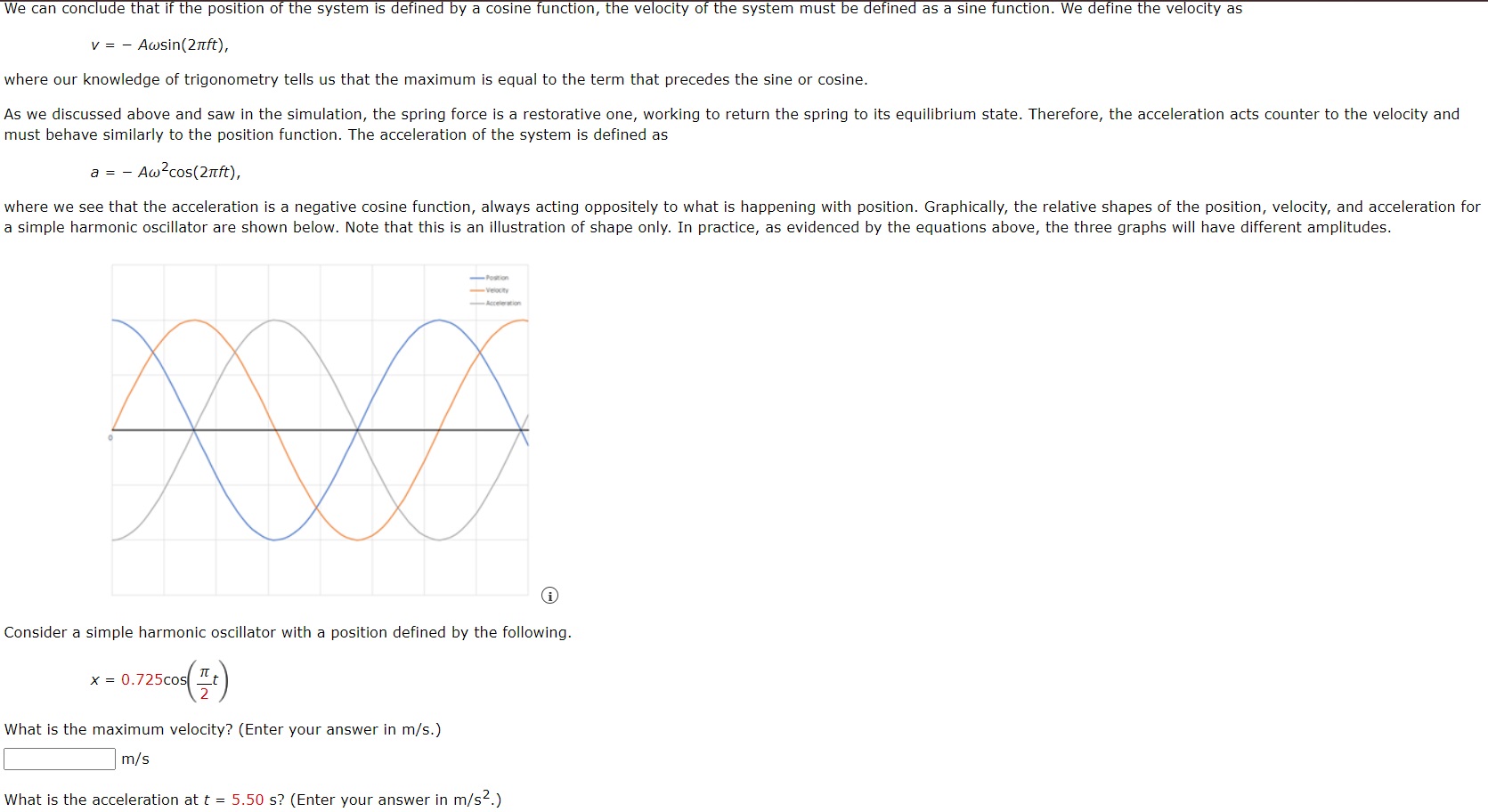
We can conclude that if the position of the system is defined by a cosine function, the velocity of the system must be defined as a sine function. We define the velocity as v = - Awsin(2ft), where our knowledge of trigonometry tells us that the maximum is equal to the term that precedes the sine or cosine. As we discussed above and saw in the simulation, the spring force is a restorative one, working to return the spring to its equilibrium state. Therefore, the acceleration acts counter to the velocity and must behave similarly to the position function. The acceleration of the system is defined as a = - Awcos(2ft), where we see that the acceleration is a negative cosine function, always acting oppositely to what is happening with position. Graphically, the relative shapes of the position, velocity, and acceleration for a simple harmonic oscillator are shown below. Note that this is an illustration of shape only. In practice, as evidenced by the equations above, the three graphs will have different amplitudes. XX i Consider a simple harmonic oscillator with a position defined by the following. x = 0.725cos 25 cos(2t) What is the maximum velocity? (Enter your answer in m/s.) m/s What is the acceleration at t = 5.50 s? (Enter your answer in m/s.)