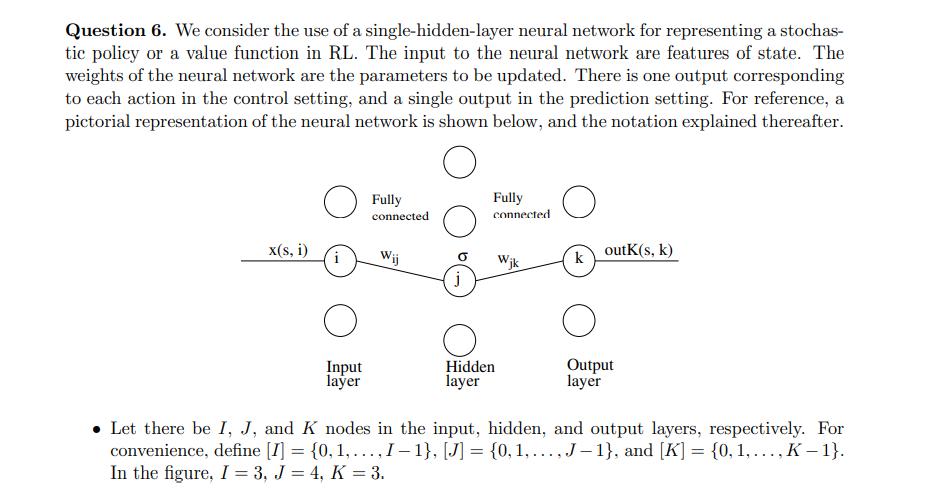
We consider the use of a single-hidden-layer neural network for representing a stochas- tic policy or a value function in RL. The input to the neural network are features of state. The weights of the neural network are the parameters to be updated. There is one output corresponding to each action in the control setting, and a single output in the prediction setting. For reference, a pictorial representation of the neural network is shown below, and the notation explained thereafter. x(s, i) i O Input layer Fully connected Wij O j Fully connected O Hidden layer O k outk(s, k) Output layer Let there be I, J, and K nodes in the input, hidden, and output layers, respectively. For convenience, define [I] = {0, 1,..., I-1}, [J] = {0, 1,.... J-1}, and [K] = {0, 1,..., K-1}. In the figure, I = 3, J = 4, K = 3. For states and i E [I], let xr(s, i) denote the i-th feature of state. The input layer merely passes on its input to output. Hence, for states and i [I], we have outI (s, i) = x(s, i). Every j-th node in the hidden layer linearly combines the outputs of the input layer, and passes the weighted sum through the sigmoid function (3) = 1 for 3 R. Thus, for states and j [J], out J(s, j) = o(ie[1] Wijout I (s, i)). Observe that there is a weight wij connecting each input node i E [I] with each hidden node j [J]. Every k-th node in the output layer corresponds to an action (hence take the set of actions as [K]). Node k [K] linearly combines the outputs of the hidden layer. Thus, for state s and k = [K], out K(s, k) = je[J] Wikout.J(s, j). Again, there is a weight wjk connecting each hidden node je [J] with each output node k [K]. For uniformity of notation, think of the prediction task as having a single action (implemented by taking K = 1). The parameters of the representation are the weights wij for i E [I], j [J] and the weights Wjk for j = [J], k [K]; in pseudocode you are asked to provide for this question (see below), store these parameters in 2-d arrays wIJ[][] and wJK[][], respectively. You can also assume that functions x(,), outI(,), outJ(,), out K(...), and o(.) are already implemented. 6a. A stochastic policy is implemented using the "soft-max" operator on the outputs of the neural network. Thus, for state s, the probability of selecting action k = [K] is eout K(s,k) k'E[K] eout K(s,k') Suppose the current policy is parameterised by weights wIJ[][] and wJK[][]. Say an episode s[0], a[0], r[0], s[1], a[1], r[1], s[2], ..., s[T] is generated by following , where s[T] is a terminal state. Write down pseudocode to perform a REINFORCE update with step size a. You can assume wIJ[][], wJK[][], T, s[], a[], r[], and a are already populated. Your code must terminate with wIJ[][] and w.JK[][] updated as per the REINFORCE rule at the end of the episode. Since you will need to compute a gradient for making the update, show the steps to work out the actual form of the gradient before presenting the pseudocode for the update. [6 marks]. 6b. Suppose the same neural network is used to approximate a value function for a prediction task. In this case we have a single output (that is, K = 1). For each state s, out K(s, 0) is interpreted as V(s). The aim is to drive V towards V" by making TD(0) updates, where is the policy being followed. Suppose the current approximation of V uses weights wIJ[][] and wJK[][]. Say the transition s, r, s' is observed. Write down pseudocode for the TD (0) update performed upon reaching s', with learning rate a and discount factory. Assume wIJ[][], wJK[][], s, r, s', a, and y are already populated. Your code must terminate with wIJ[][] and wJK[][] updated correctly. Here, too, show the steps to obtain the form of the gradient before using it in your pseudocode as a part of the learning update. Since K = 1, you can use wJK[] instead of wJK[][] if you would like, but the 2-dimensional variant is also okay, keeping the second index 0. [3 marks].