Question
We don't need the much work shown: This is the rubric: https://docs.google.com/presentation/d/e/2PACX-1vTfv8W7MfhU_0gF-ZPeJ1JoJh2LDQmYIIvCZopQuzhgqZ8vI8zNXQmcooN9zKsnz507Ilr9P6vQkAib/embed?start=false&loop=false&delayms=3000&rm=minimal&slide=id.p references: (5.01)Defining Trigonometric Functions and Their Angles Segment: 2 (5.02) Law of Sines
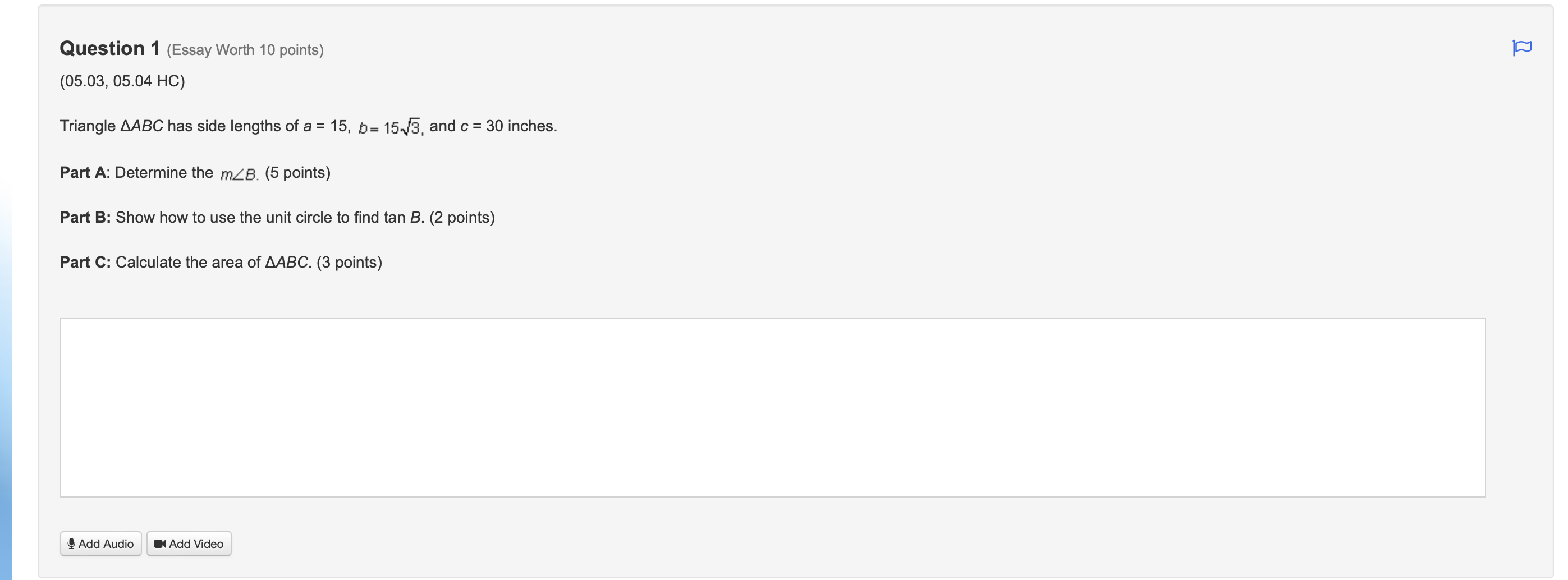
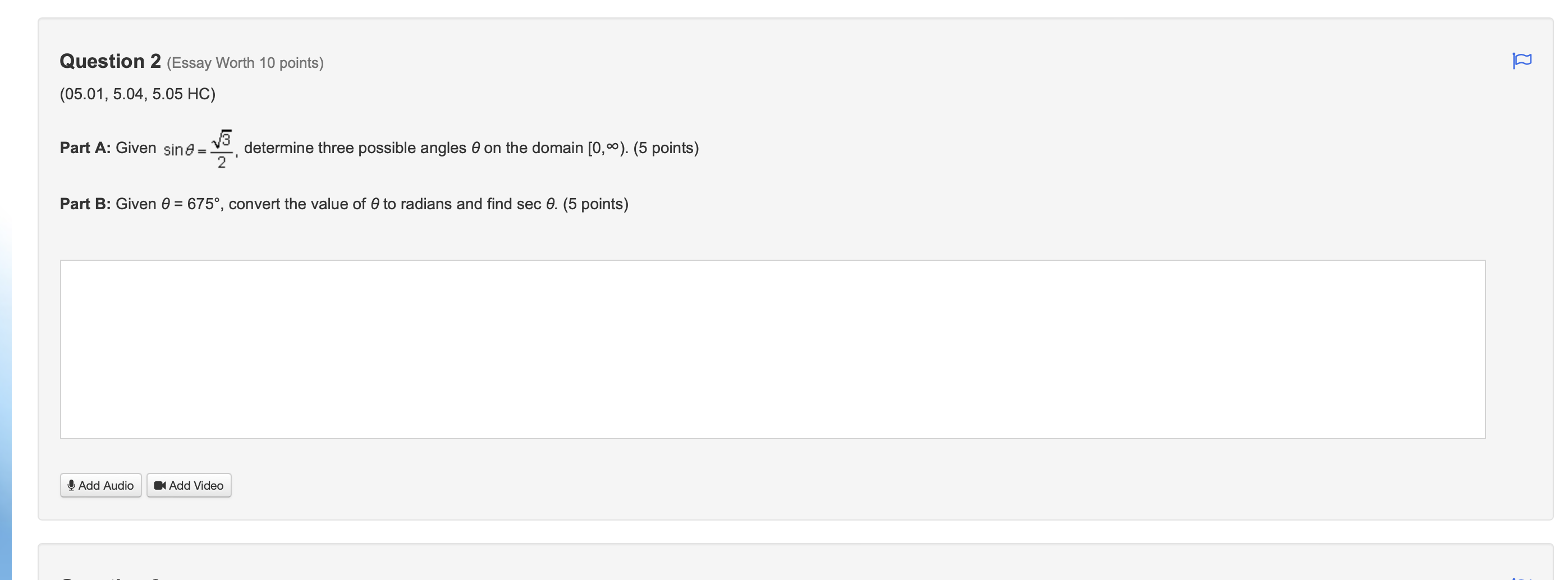
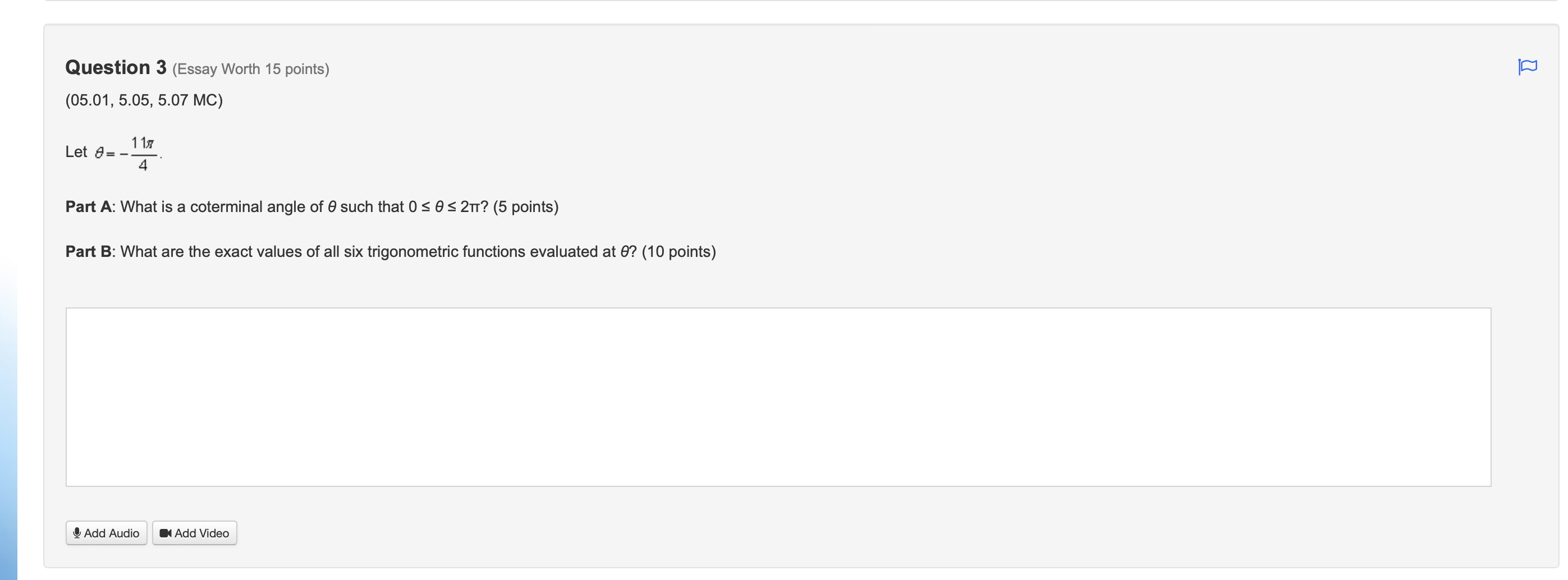
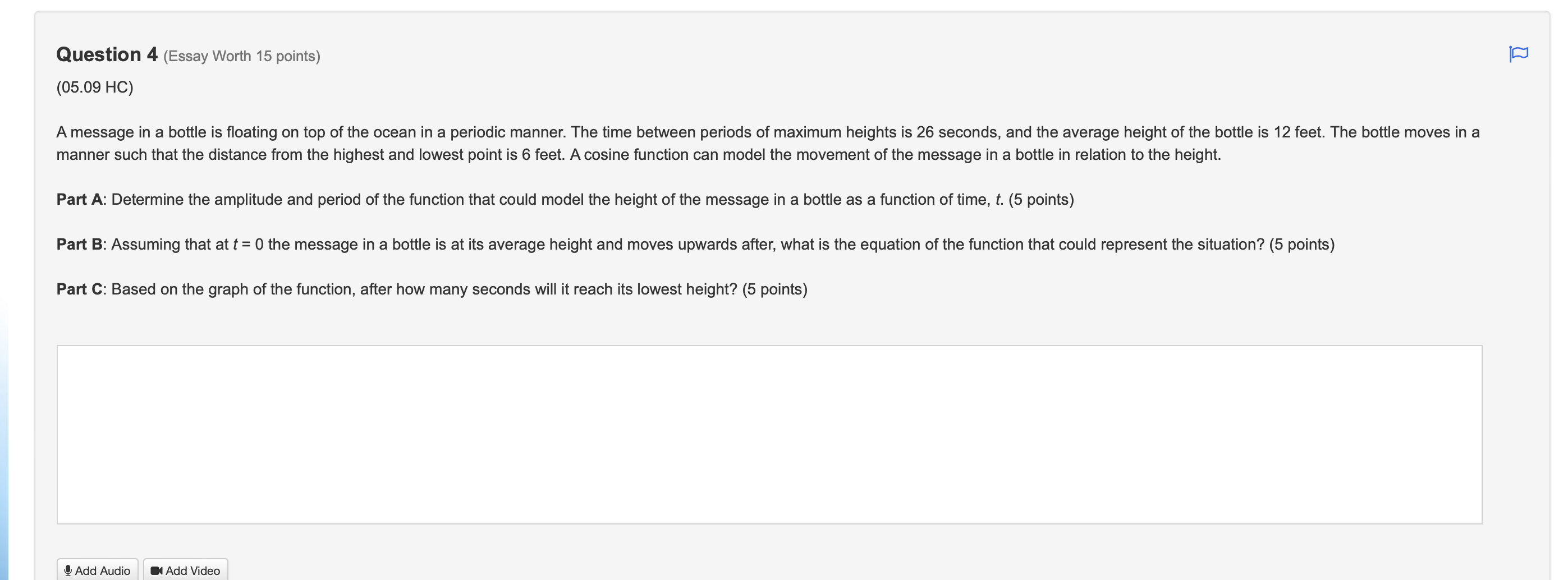
We don't need the much work shown: This is the rubric: https://docs.google.com/presentation/d/e/2PACX-1vTfv8W7MfhU_0gF-ZPeJ1JoJh2LDQmYIIvCZopQuzhgqZ8vI8zNXQmcooN9zKsnz507Ilr9P6vQkAib/embed?start=false&loop=false&delayms=3000&rm=minimal&slide=id.p references: (5.01)Defining Trigonometric Functions and Their Angles Segment: 2 (5.02) Law of Sines Segment: 2 (5.03) Law of Cosines Segment: 2 (5.04) Unit Circle Segment: 2 (5.05) Making the Unit Circle Work for You Segment: 2 (5.06) Trigonometry Mid-Module Check Segment: 2 (5.07) Graphing the Sine and Cosine Functions Segment: 2 (5.08) Graphing Other Trigonometric Functions Segment: 2 (5.09) Analyzing Trigonometry function and graphs
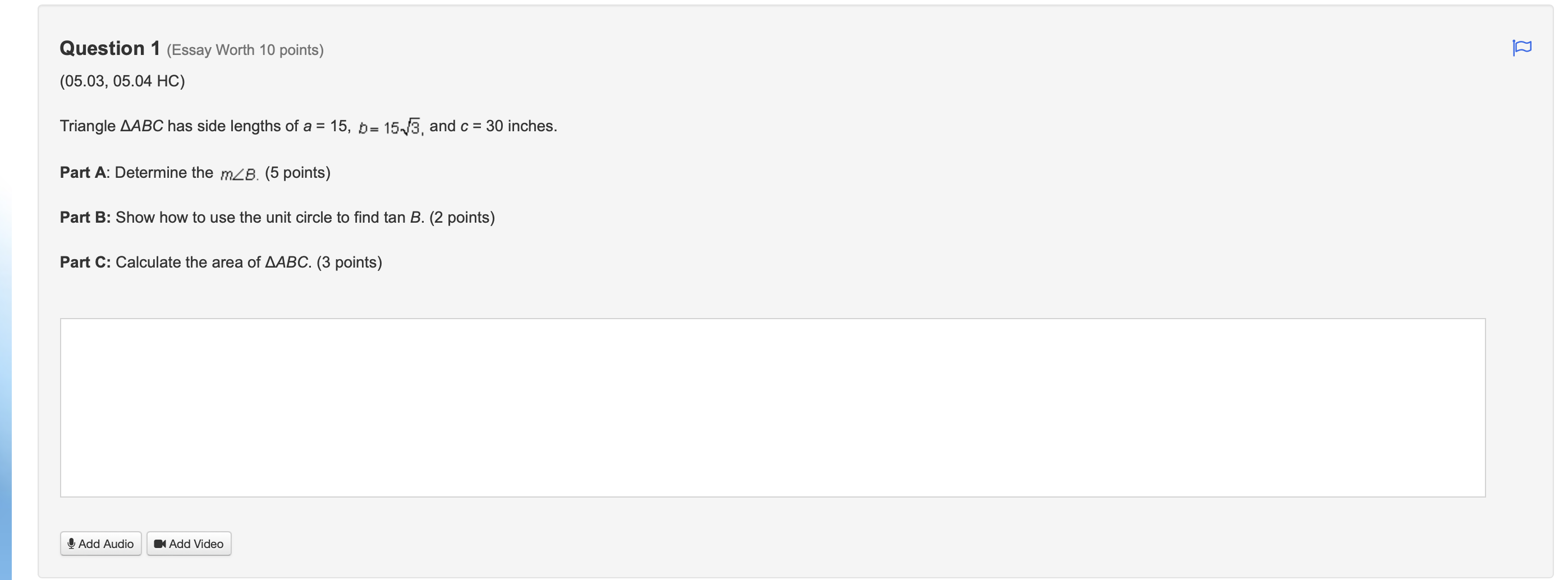
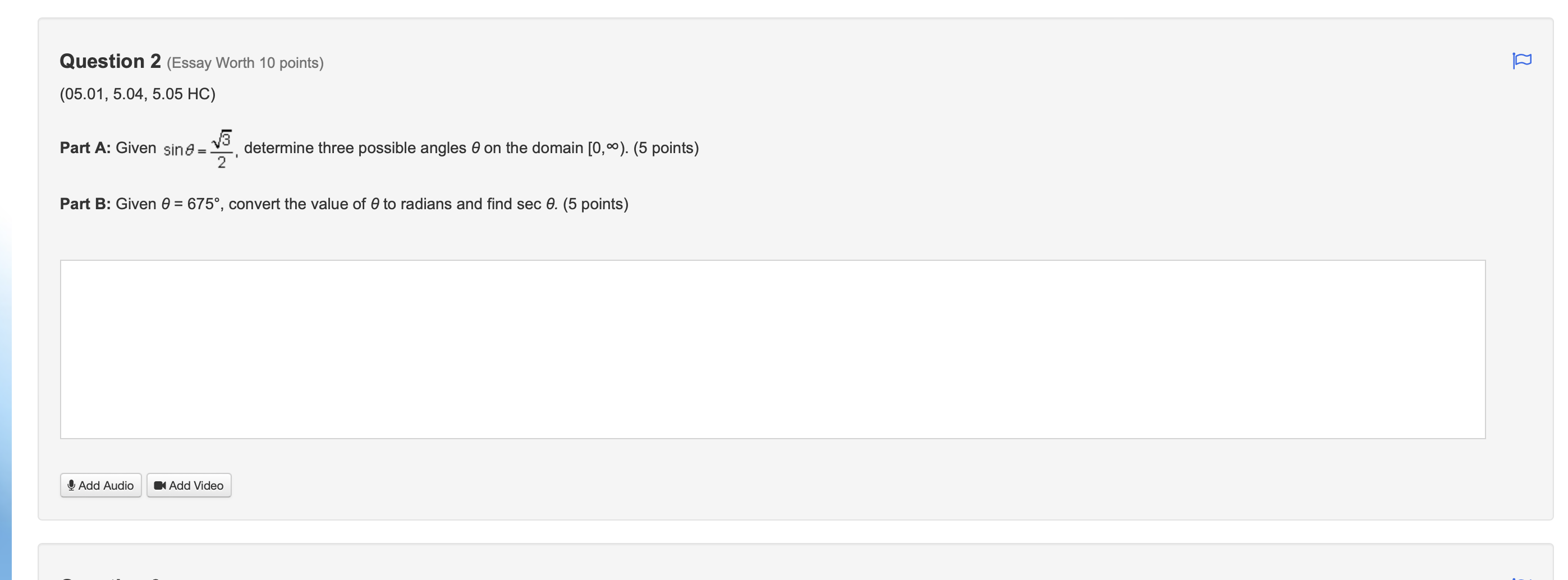
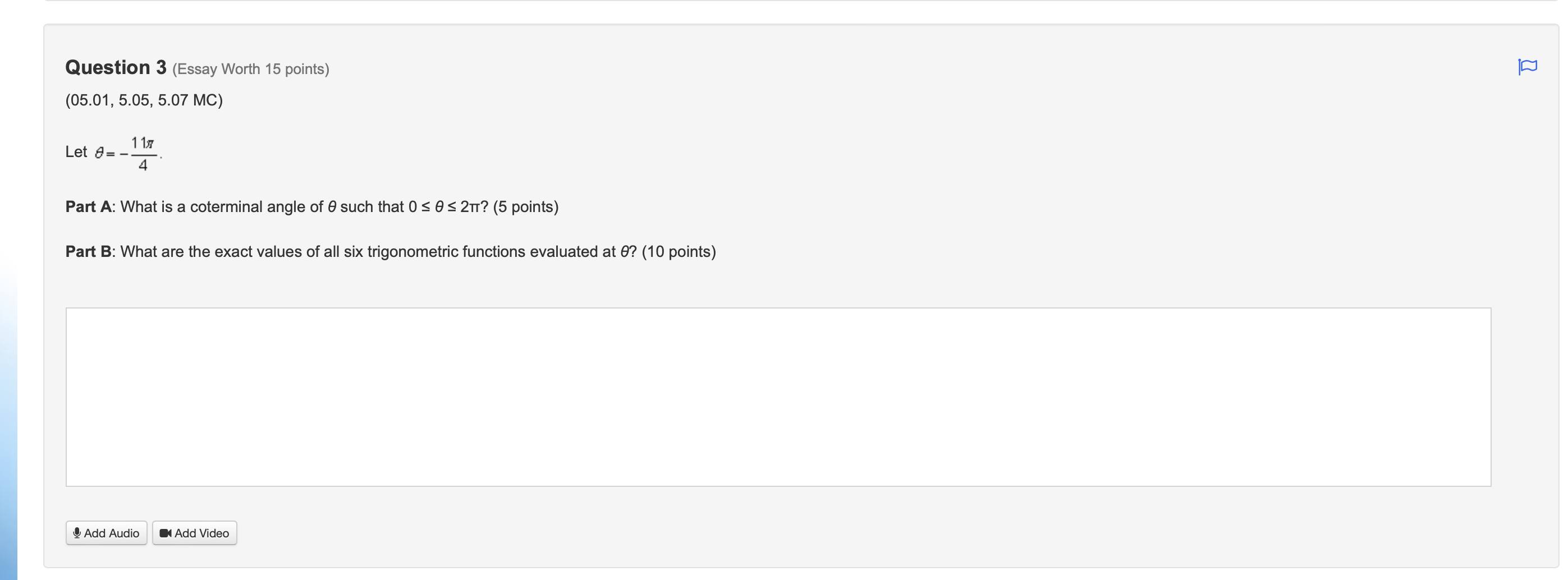
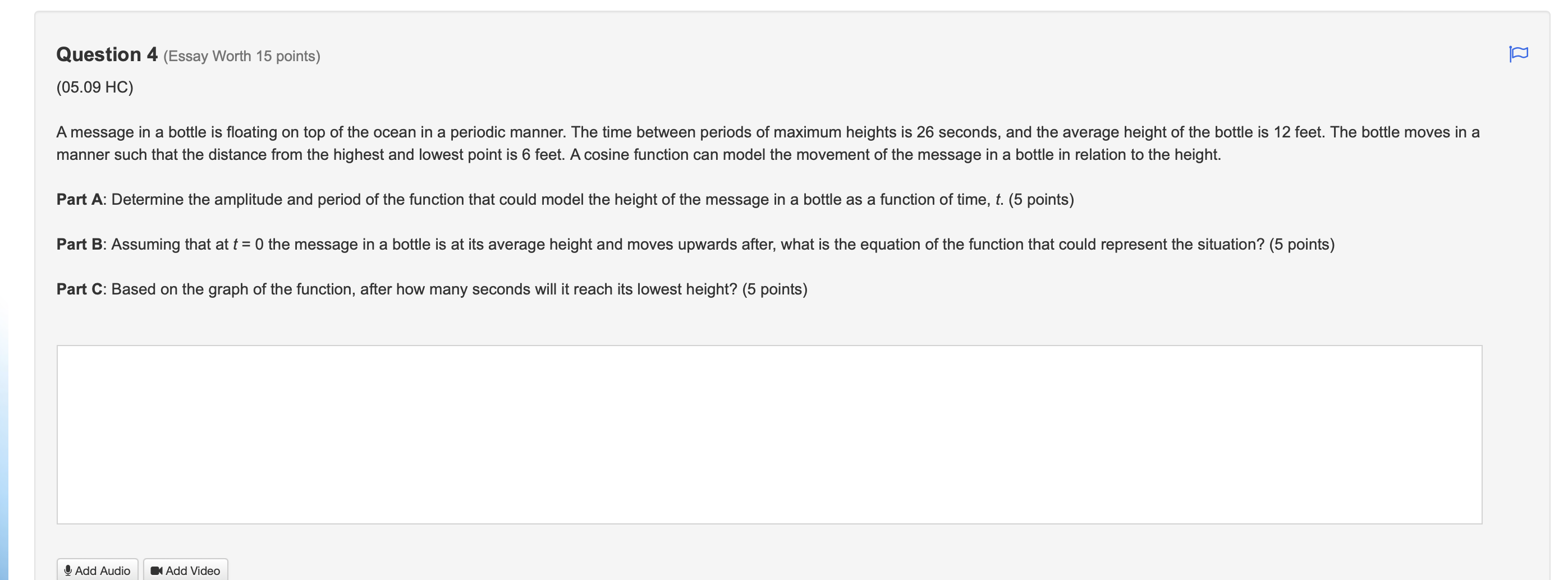
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


