Well, the problem is in the picture, it may cause a little reading difficulty? thank you very much
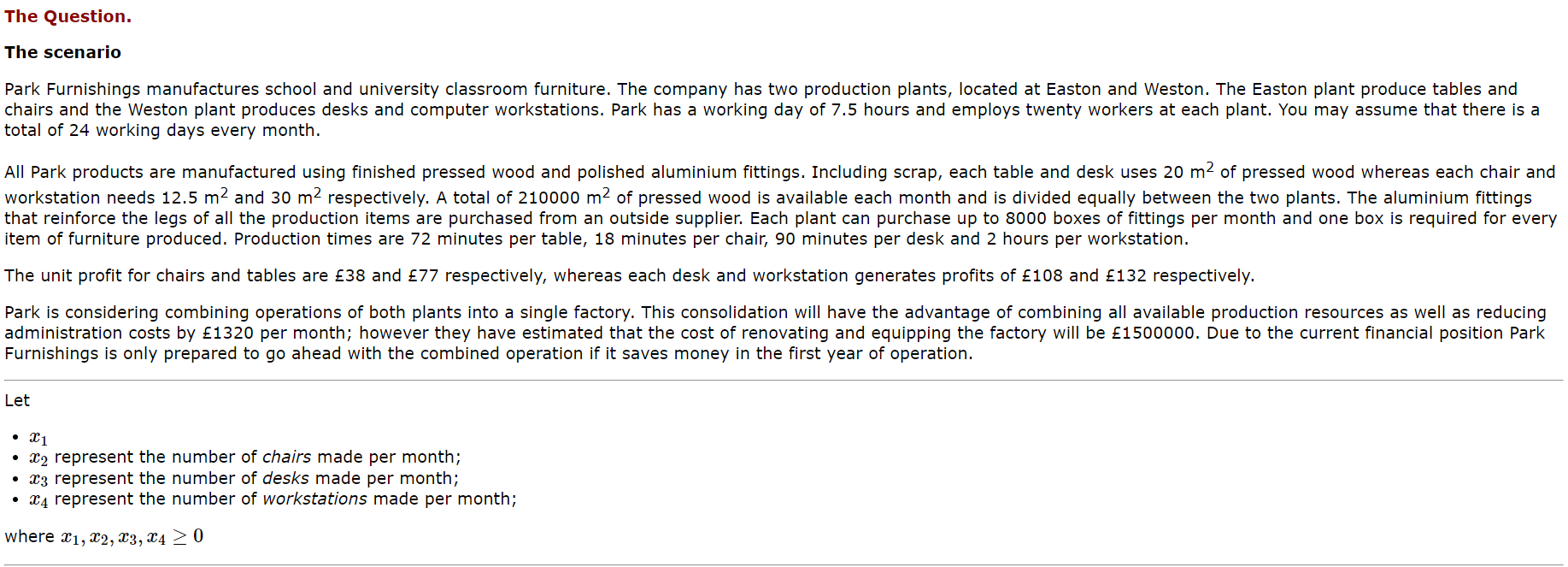
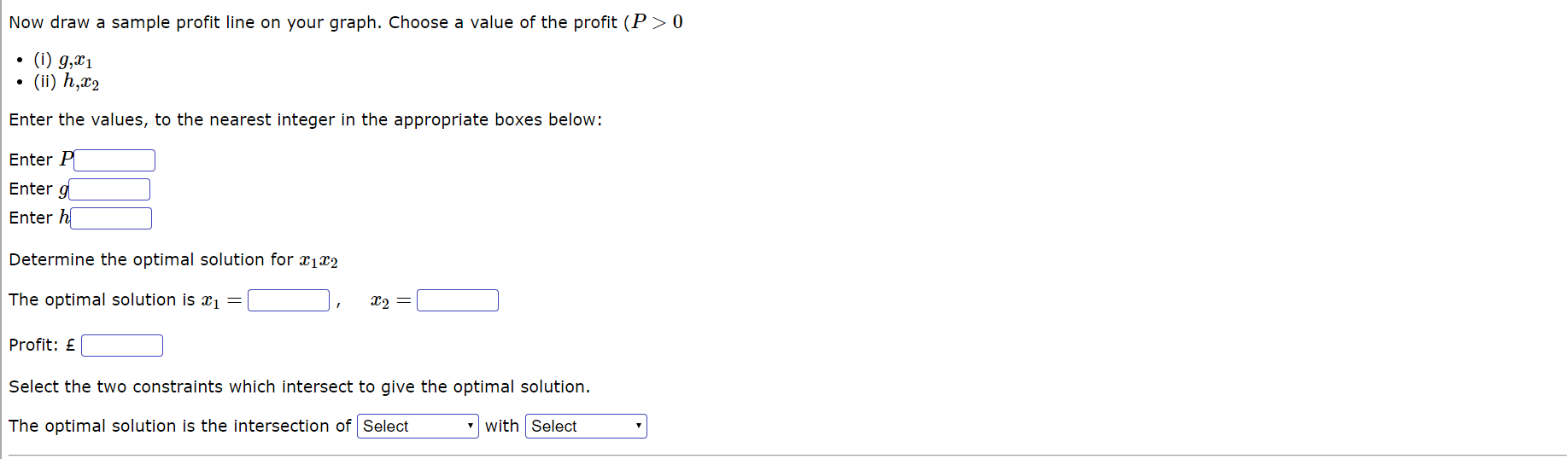
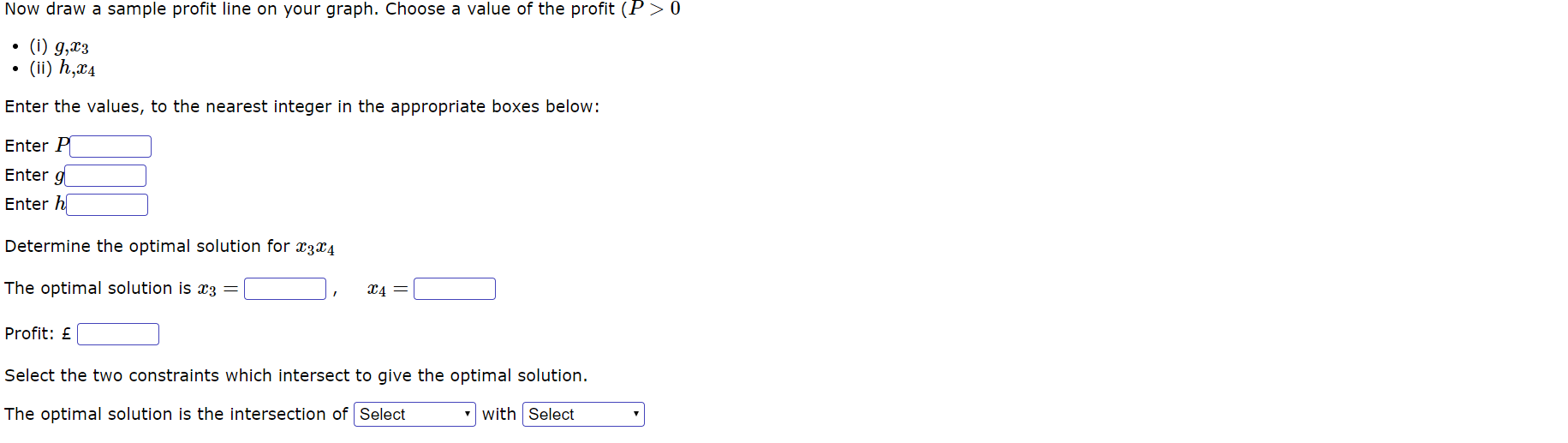
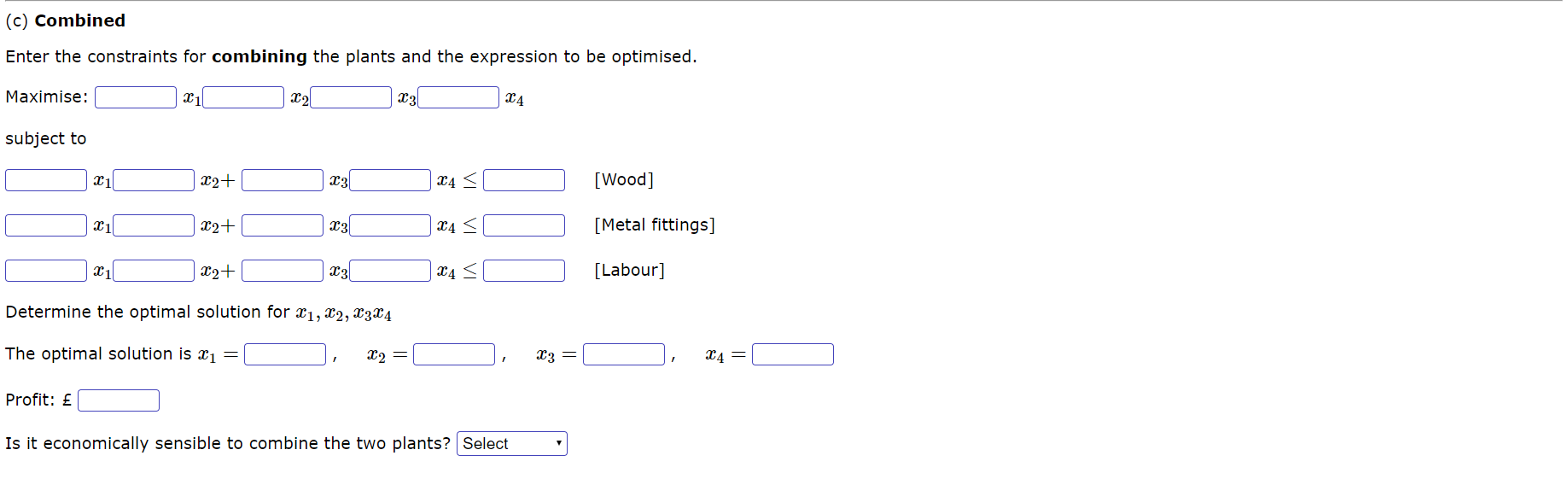
The Question. The scenario Park Furnishings manufactures school and university classroom furniture. The company has two production plants, located at Easton and Weston. The Easton plant produce tables and chairs and the Weston plant produces desks and computer workstations. Park has a working day of 7.5 hours and employs twenty workers at each plant. You may assume that there is a total of 24 working days every month. All Park products are manufactured using finished pressed wood and polished aluminium fittings. Including scrap, each table and desk uses 20 m2 of pressed wood whereas each chair and workstation needs 12.5 rn2 and 30 m2 respectively. A total of 210000 m2 of pressed wood is available each month and is divided equally between the two plants. The aluminium fittings that reinforce the legs of all the production items are purchased from an outside supplier. Each plant can purchase up to 8000 boxes of ttings per month and one box is required for every item of furniture produced. Production times are 72 minutes per table, 18 minutes per chair, 90 minutes per desk and 2 hours per workstation. The unit profit for chairs and tables are 38 and 77 respectively, whereas each desk and workstation generates profits of 108 and 132 respectively. Park is considering combining operations of both plants into a single factory. This consolidation will have the advantage of combining all available production resources as well as reducing administration costs by 1320 per month; however they have estimated that the cost of renovating and equipping the factory will be 1500000. Due to the current financial position Park Furnishings is only prepared to go ahead with the combined operation if it saves money in the first year ofoperation. Let a {15-1 - 932 represent the number of chairs made per month; - :03 represent the number of desks made per month; - 934 represent the number of workstations made per month; where {choke-3,34 Z 0 ( a ) Easton Enter the constraints for the Easton plant and the expression to be optimised . Maximise : \\\\ Jal + \\ | 2'2 subject to Jal + \\\\ [ Wood ] Jal + \\ Jaz SL [ Metal fittings ] | al + \\ [ Labour ] sketch the constraints and hence find the values of . ( 1 ) a , 6 , Call . ( 1 1) d, e , f , acz Enter the values , to the nearest integer in the appropriate boxes below :" Enter a Enter b| Enter a Enter d Enter el Enter A Now draw a sample profit line on your graph . Choose a value of the profit ( P > O . ( 1 ) 9 , * 1 . ( 11 ) 1, 212Now draw a sample prot line on your graph. Choose a value of the profit (P > 0 ' (09,51 W) hit"? Enter the values, to the nearest integer in the appropriate boxes below: were: Entergl:] Enterhi:] Determine the optimal solution for 2:11;; The optimal solution is 11:1 : [:] , 2:2 : [:] Profit: :] Select the two constraints which intersect to give the optimal solution. The optimal solution is the intersection of with (b) Weston Enter the constraints for the Weston plant and the expression to be optimised. Maximise: [:] 13:] 5134 subject to [:1 33:1 904 S [:1 [Wood] :1 #4:] m4 2 :] [Metal fittings] :1 $3:1 $4 5 :1 [Labour] Sketch the constraints and hence nd the values of ' (i) 0., b1 C7933 ' (ii) dzewfh: Enter the values, to the nearest integer in the appropriate boxes below: Enter 0:] Enter ll: Enter '11:] Enter 01:] Enter E Enter :] Now draw a sample prot line on your graph. Choose a value of the profit (P > 0 ' (i) .9733 ' (ii) hm Now draw a sample prot line on your graph. Choose a value of the profit (P > 0 ' (09,933 ' (ii) M34 Enter the values, to the nearest integer in the appropriate boxes below: EnterH:1 EnterQi:] Enrer 11:] Determine the optimal solution for $3324 The optimal solution is 1:3 : C] , m4 : :] Profit: s :] Select the two constraints which intersect to give the optimal solution. The optimal solution is the intersection of with ( C ) Combined Enter the constraints for combining the plants and the expression to be optimised . Maximise :" Jail Jacal Jac3\\ subject to Jazzt L 123\\ [ Wood ] Jazz t L Jac3\\ [ Metal fittings] Jac3\\ [ Labour ] Determine the optimal solution for *1 , 202 , 203 .0 4 The optimal solution is *1 = \\ 202 = \\ 2:3 = [ 2 4 = [ Profit : E Is it economically sensible to combine the two plants ? | Select*