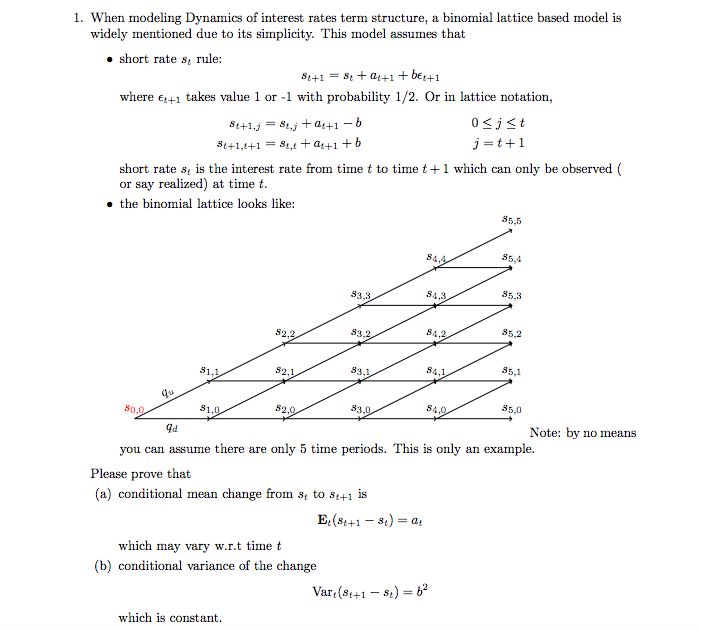

When modeling Dynamics of interest rates term structure, a binomial lattice based model is widely mentioned due to its simplicity. This model assumes that short rate s_t rule: s_t + 1 = s_t + a_t + a_t + 1 + b_elementof_t + 1 where elementof_t + 1 takes value 1 or -1 with probability 1/2. Or in lattice notation, s_t + 1, j = s_t, j + a_t + 1 - b 0 lessthanorequalto j lessthanorequalto t s_t + 1, t + 1 = s_t, t + a_t + 1 + b j = t + 1 short rate s_t is the interest rate from time t to time t + 1 which can only be observed (or say realized) at time t. the binomial lattice looks like: Please prove that (a) conditional mean change from s_t to s_t + 1 is E_t(s_t + 1 - s_t) = a_t which may vary w.r.t time t (b) conditional variance of the change Var_t(s_t + 1 - s_t) = b^2 which is constant. (c) in some discussion, researchers will use a slightly different notation. s_i, j = a'_i + b'j, where 0 lessthanorequalto j lessthanorequalto i please find the relationship between the two different notations. (d) The observed interest rate term structure is (7.3, 7.62, 8.1, 8.45, 9.2, 9.64, 10.12, 10.45, 10.75, 11.22, 11.55, 11.92, 12.2, 12.32). Settings q_u = q_d = 0.5 and b = 0.5 for simplicity, find the appropriate a_i's such that the sum of squared error (SSE) between observed interest rate term structure and implied interest rate term structure. Let r_i stand for the observed interest rate from time 0 to time i, from the binomial lattice described above. Then he SSE can be expressed as SSE = sigma_i (r_i - m_i)^2 You can use the excel solver or RQuadprog in R or anything else to solve the problem. Do the computed a_i' s depend on the choice of q_u, q_d or b? (e) Suppose there is an callable bond with coupon rate 9.5% in the market which can be called back in 3 years at strike price exist100. Coupons are paid annually, the fact: value is exist100 and maturity is 9 years. If the bond is called back, the secured interest rate should also be paid. Please compute the price of the callable bond with the default setting above and proper a_i' s computed. Does the computed no-arbitrage price of the callable bond depends on the choice of b or q_u or both? What does b in the model stand for? (f) There is a capped floater (floating coupon rate bond with upper bond on the coupon rate) in the market. Its maturity is 10 years. The bond's coupon rate is reset every year according to "coupon rate = min(prevailing risk-free 1-year spot rate +10 bps, 13%)". Suppose the coupon is paid annually. What is the no arbitrage price of the floater under observed spot rates term structure and parameters given above. Suppose there is no default risk








