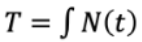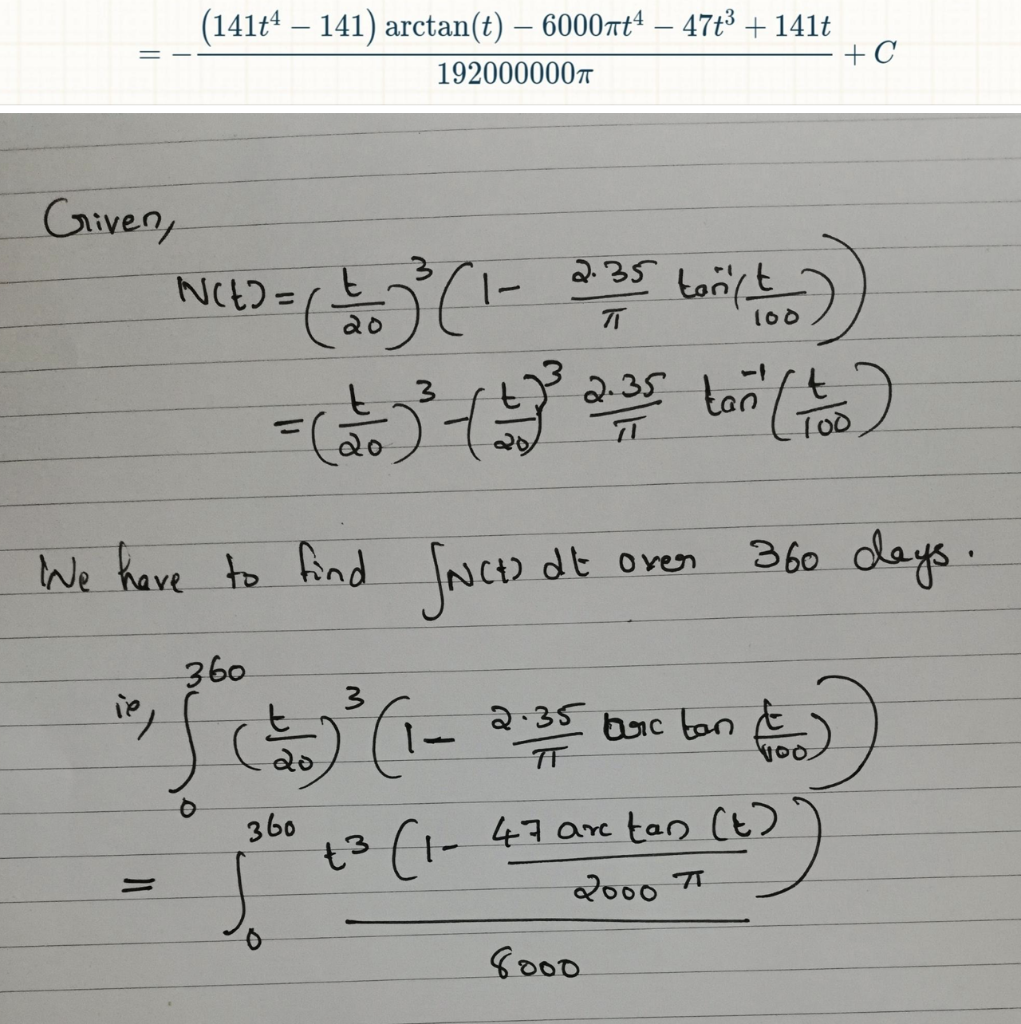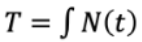
where
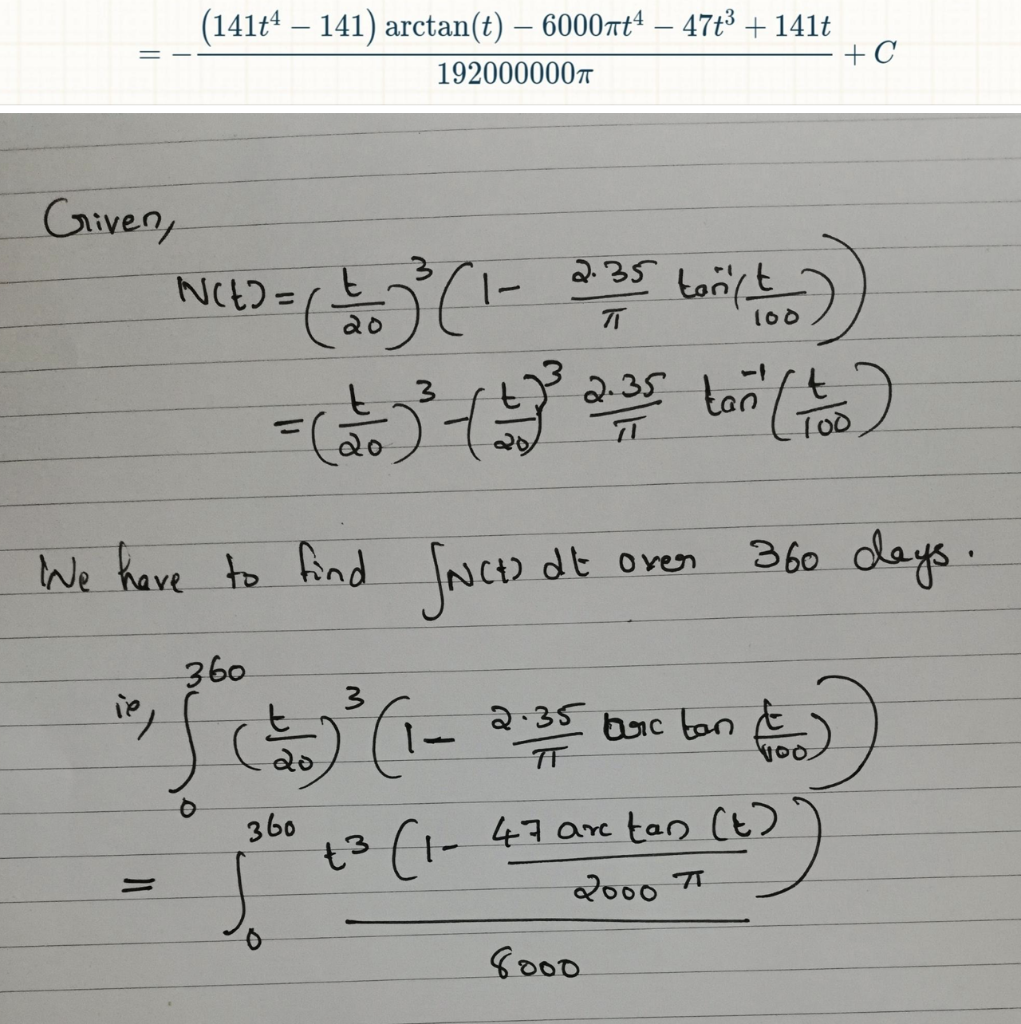
11.4 9 pts Programming: Trapezoid and Simpsons method in MATLAB Calculate the total number of infections T using two methods (Trapezoid, Simpsons-1/3), by writing three functions to run off one MATLAB script: a) Function 1: f = Fun(x), the function that outputs the integrand (i.e. the "thing" that is to be integrated from 0 to 360 days). You already wrote this in problem 11.2. Done!! b) Function 2: Itrap = Trapez (a,b,n) that outputs the integral of Fun (x) over [a,b] using n nodes with the Trapezoid rule. c) Function 3: Isimp = Simpson (a, b,n) that outputs the integral of Fun (x) over [a,b] using n nodes with the Simpsons rules. Make your function easier by assuming that the number of nodes n will always be odd, so you'll only need to program the -1/3 rule. d) Script: Write an m-file called Quaddy.m that ... i. Calls Trapez multiple times to evaluate T using the trapezoid method for each of the following number of nodes: n = [5 21 201 2001 20,001 200,001). ii. Similarly calls Simpson to evaluate I for the same six values of nodes above, that is n = [5 21 201 2001 20,001 200,001). iii. Uses the exact" value of I from 11.2 (with ALL its decimals) to calculate the percent (relative) error for all the approximations of Tin (i) and (ii). iv. Uses the loglog function to plot the log 10 of the absolute value of the % relative error from (i) & (ii) as a function of log 10 of the interval size, h. When done I expect to see two lines on the plot: one line for each method (Trapezoid & Simpsons), each with six values of h, similar to the plot I showed and discussed (and posted!) in Class 26. Please make each line different, so the trapezoid method shows squares connected by solid red line, and the Simpsons method shows circles connected by dashed blue lines. Be sure to use the loglog plot command to allow details to be seen even when the error gets very small. So, use something like this plot command: loglog (h, PctErrTrapez,'sr-', h, PctErrSimpson,'ob--') Save this plot in pdf form as Quad.pdf, and submit all your files online: Codes Fun.m, Trapez.m, Simpson.m, Quaddy.m, and plot Quad.pdf Now, look at the plot: you should be seeing your error get small as h gets smaller. BY HAND, please write up answers to the following two questions: e) Read values off the axes (by hand) to evaluate the slope of the Trapezoid error line in log-log space (i.e. the slope of log(Error) vs. log(h), like we discussed in class). Explain whether that slope is consistent with your expectations from class. (What do you expect? What do you see?) f) Look at the shape & slope(s) of the Simpsons line. Explain whether that is consistent with your expectation of shape & slope from class. (What do you expect? What do you see?) You probably see a "kink in the line as h gets "too" small. Based on everything you've been learning all year, explain what you think is happening here to cause this kink. T = S N(t) (141t4 141) arctan(t) 60001t4 47+3 + 1410 1920000001 +C Griven, INCE2=t 2.35 tow' (to) dt over 360 days. We have to find facto .35 buc ton to 360 3 2.35 TT do 360 +3 (1- 47 are tan (6) " 2000 71 0 8000 11.4 9 pts Programming: Trapezoid and Simpsons method in MATLAB Calculate the total number of infections T using two methods (Trapezoid, Simpsons-1/3), by writing three functions to run off one MATLAB script: a) Function 1: f = Fun(x), the function that outputs the integrand (i.e. the "thing" that is to be integrated from 0 to 360 days). You already wrote this in problem 11.2. Done!! b) Function 2: Itrap = Trapez (a,b,n) that outputs the integral of Fun (x) over [a,b] using n nodes with the Trapezoid rule. c) Function 3: Isimp = Simpson (a, b,n) that outputs the integral of Fun (x) over [a,b] using n nodes with the Simpsons rules. Make your function easier by assuming that the number of nodes n will always be odd, so you'll only need to program the -1/3 rule. d) Script: Write an m-file called Quaddy.m that ... i. Calls Trapez multiple times to evaluate T using the trapezoid method for each of the following number of nodes: n = [5 21 201 2001 20,001 200,001). ii. Similarly calls Simpson to evaluate I for the same six values of nodes above, that is n = [5 21 201 2001 20,001 200,001). iii. Uses the exact" value of I from 11.2 (with ALL its decimals) to calculate the percent (relative) error for all the approximations of Tin (i) and (ii). iv. Uses the loglog function to plot the log 10 of the absolute value of the % relative error from (i) & (ii) as a function of log 10 of the interval size, h. When done I expect to see two lines on the plot: one line for each method (Trapezoid & Simpsons), each with six values of h, similar to the plot I showed and discussed (and posted!) in Class 26. Please make each line different, so the trapezoid method shows squares connected by solid red line, and the Simpsons method shows circles connected by dashed blue lines. Be sure to use the loglog plot command to allow details to be seen even when the error gets very small. So, use something like this plot command: loglog (h, PctErrTrapez,'sr-', h, PctErrSimpson,'ob--') Save this plot in pdf form as Quad.pdf, and submit all your files online: Codes Fun.m, Trapez.m, Simpson.m, Quaddy.m, and plot Quad.pdf Now, look at the plot: you should be seeing your error get small as h gets smaller. BY HAND, please write up answers to the following two questions: e) Read values off the axes (by hand) to evaluate the slope of the Trapezoid error line in log-log space (i.e. the slope of log(Error) vs. log(h), like we discussed in class). Explain whether that slope is consistent with your expectations from class. (What do you expect? What do you see?) f) Look at the shape & slope(s) of the Simpsons line. Explain whether that is consistent with your expectation of shape & slope from class. (What do you expect? What do you see?) You probably see a "kink in the line as h gets "too" small. Based on everything you've been learning all year, explain what you think is happening here to cause this kink. T = S N(t) (141t4 141) arctan(t) 60001t4 47+3 + 1410 1920000001 +C Griven, INCE2=t 2.35 tow' (to) dt over 360 days. We have to find facto .35 buc ton to 360 3 2.35 TT do 360 +3 (1- 47 are tan (6) " 2000 71 0 8000