Why is using a three-level Manhattan more efficient than using a Manhattan with long indel edges to solve the Alignment with Affine Gap Penalties Problem?



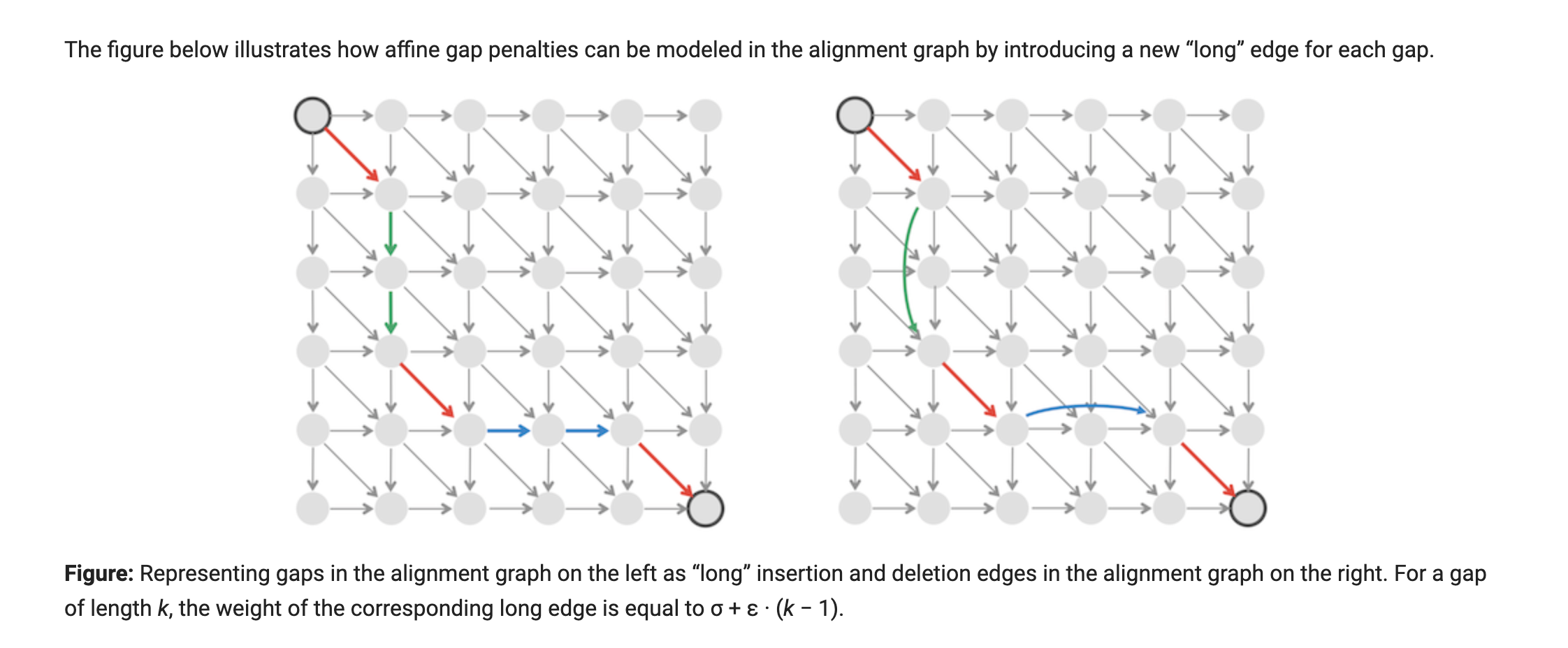
Building Manhattan on three levels The trick to decreasing the number of edges in the DAG for the Alignment with Affine Gap Penalties Problem is to increase the number of nodes. To this end, we will build an alignment graph on three levels; for each node (ij), we will construct three different nodes: (Dlower. (D) middle, and (1. jupper. The middle level will contain diagonal edges of weight score(vi, W;) representing matches and mismatches. The lower level will have only vertical edges with weight - to represent gap extensions in v, and the upper level will have only horizontal edges with weights -e to represent gap extensions in w (see figure below). Figure: Building a three-level graph for alignment with affine gap penalties. The lower level corresponds to gap extensions in v, the middle level corresponds to matches and mismatches, and the upper level corresponds to gap extensions in w. Life in such a three-level city would be difficult because there is currently no way to move between different levels. To address this issue, we add edges responsible for opening and closing gaps. To model gap opening, we connect each node 1, Dmiddle to both (i + 1. Dlower and (1.j + 1)upperi we then weight these edges with -o. Closing a gap does not carry a penalty, and so we introduce zero-weight edges connecting nodes (i, Dlower and (i, Dupper with the corresponding node (1, 1)middle at the middle level. As a result, a gap of length k starts and ends at the middle level and is charged -o for the first symbol, -e for each subsequent symbol, and 0 to close the gap, producing a total penalty of o + . (k-1), as desired. The figure below illustrates how the path from this lesson's third step traverses the three-level graph. Exercise Break: Prove that the number of edges in the three-level graph described in the figure below is at most 7.n.m for sequences of length n and m. 611 best II The DAG we have just constructed may be complicated, but it uses only O(n. m) edges for sequences of length n and m, and a longest path in this graph still constructs an optimal alignment with affine gap penalties. The three-level alignment graph translates into the system of three recurrence relations shown below. Here, loweri,j, middlej,j, and upperi,j, are the lengths of the longest paths from the source node to (i, j)lower, (i, j) middle, and (i, jupper, respectively. lower;-1,j - lowerij = max middle;1,j 0 upperi,j-1 - 6 upperij = max | middle;,j-10 lowerij middlei,j = max { middle;1,11 + score(Vi,W;) | upperij The variable lowerij computes the score of an optimal alignment between the i-prefix of v and the j-prefix of w ending with a deletion (i.e., a vertical edge), whereas the variable upperij computes the score of an optimal alignment of these prefixes ending with an insertion (i.e., a horizontal edge), and the variable middlei,j computes the score of an optimal alignment ending with a match or mismatch. The first term in the recurrences for loweri,j and upperi,j corresponds to extending the gap, whereas the second term corresponds to initiating the gap. The figure below illustrates how affine gap penalties can be modeled in the alignment graph by introducing a new long" edge for each gap. Figure: Representing gaps in the alignment graph on the left as long insertion and deletion edges in the alignment graph on the right. For a gap of length k, the weight of the corresponding long edge is equal to 0 + (k-1). Building Manhattan on three levels The trick to decreasing the number of edges in the DAG for the Alignment with Affine Gap Penalties Problem is to increase the number of nodes. To this end, we will build an alignment graph on three levels; for each node (ij), we will construct three different nodes: (Dlower. (D) middle, and (1. jupper. The middle level will contain diagonal edges of weight score(vi, W;) representing matches and mismatches. The lower level will have only vertical edges with weight - to represent gap extensions in v, and the upper level will have only horizontal edges with weights -e to represent gap extensions in w (see figure below). Figure: Building a three-level graph for alignment with affine gap penalties. The lower level corresponds to gap extensions in v, the middle level corresponds to matches and mismatches, and the upper level corresponds to gap extensions in w. Life in such a three-level city would be difficult because there is currently no way to move between different levels. To address this issue, we add edges responsible for opening and closing gaps. To model gap opening, we connect each node 1, Dmiddle to both (i + 1. Dlower and (1.j + 1)upperi we then weight these edges with -o. Closing a gap does not carry a penalty, and so we introduce zero-weight edges connecting nodes (i, Dlower and (i, Dupper with the corresponding node (1, 1)middle at the middle level. As a result, a gap of length k starts and ends at the middle level and is charged -o for the first symbol, -e for each subsequent symbol, and 0 to close the gap, producing a total penalty of o + . (k-1), as desired. The figure below illustrates how the path from this lesson's third step traverses the three-level graph. Exercise Break: Prove that the number of edges in the three-level graph described in the figure below is at most 7.n.m for sequences of length n and m. 611 best II The DAG we have just constructed may be complicated, but it uses only O(n. m) edges for sequences of length n and m, and a longest path in this graph still constructs an optimal alignment with affine gap penalties. The three-level alignment graph translates into the system of three recurrence relations shown below. Here, loweri,j, middlej,j, and upperi,j, are the lengths of the longest paths from the source node to (i, j)lower, (i, j) middle, and (i, jupper, respectively. lower;-1,j - lowerij = max middle;1,j 0 upperi,j-1 - 6 upperij = max | middle;,j-10 lowerij middlei,j = max { middle;1,11 + score(Vi,W;) | upperij The variable lowerij computes the score of an optimal alignment between the i-prefix of v and the j-prefix of w ending with a deletion (i.e., a vertical edge), whereas the variable upperij computes the score of an optimal alignment of these prefixes ending with an insertion (i.e., a horizontal edge), and the variable middlei,j computes the score of an optimal alignment ending with a match or mismatch. The first term in the recurrences for loweri,j and upperi,j corresponds to extending the gap, whereas the second term corresponds to initiating the gap. The figure below illustrates how affine gap penalties can be modeled in the alignment graph by introducing a new long" edge for each gap. Figure: Representing gaps in the alignment graph on the left as long insertion and deletion edges in the alignment graph on the right. For a gap of length k, the weight of the corresponding long edge is equal to 0 + (k-1)










