Wk6-HW6 Confidence Intervals and Hypothesis Tests Comparing TWO Proportions, Differences or Means AND ANOVA (Analysis of Variance)

This first part of this Homework involves calculating: Confidence Interval for two population Proportions Hypothesis Test for two population Proportions Hypothesis Test for two population Differences Confidence Interval for two population differences Hypothesis Test comparing two population Means

IF you need additional guidance, there is a Supplement Guidance attachment for your use. It does relate to these problem types and should be useful in saving you time working them.

1) (made-up data) Confidence Interval Problem for Proportions: Calculate a 95% confidence interval for these proportions. SHOW YOUR "E" SETUP & CALCULATIONS. The same assumptions must be met to insure the statistical analysis is valid and Make sure to calculate the proportions first.

High school students take the AP tests in different subject areas. This year 150 students took the biology exam of which 85 were female. And, 220 students took the calculus exam of which 100 were female. Calculate the difference in the PROPORTION of female students taking the biology exam verses female students taking the calculus exam using a 95% confidence level. E = z-critical * sqrt[ (p-hat1 * q-hat1)1) + (p-hat2 * q-hat2)2)]

2) (made-up data) Hypothesis Test problem for Proportions: Assume a 1% significance level. The same assumptions must be met to insure the statistical analysis is valid and calculate the proportions first.

SHOW Z-Test SETUP AND Z-Critical value the z-Test was compared to. Also, use software to calculate the p-Value. Do both support the same conclusion? (they MUST). State your real-world conclusion?

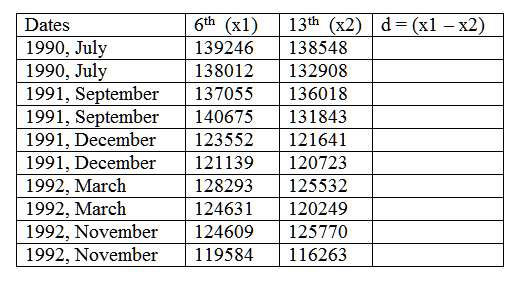
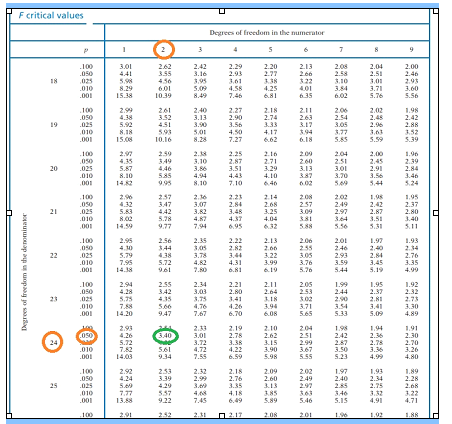
Are more children diagnosed with Autism Spectrum Disorder in States that have urban areas over States that are mostly rural? In an urban State there were are 300 3rd grade students diagnosed with ASD out of 18,500 3rd graders tested. In a rural state, there were 55 3rd grade students diagnosed with ASD out of 2,300 3rd graders tested. Is there enough evidence to show that the proportion of children diagnosed with ASD in an urban State is more than the proportion in a rural State? Test at the = 1% level. 3) Coin-Toss Data - We had ____ sets of 30-flipped coin sets. Some used ONE coin and some 30 different coins. Conduct a hypothesis test on the proportion of HEADS using ONE coin verses proportion of HEADS using 30 coins. IS there a significant difference (5% level)? t-Test = [(x-bar1 - x-bar2) - (1 - 2)] / sqrt ( s121 + s222) To find the t-Critical we need the degrees of freedom (df) and the formula to calculate df is "hairy". As presented earlier, there simpler formula that is used by some statisticians: df = (n1 - 1) + (n2 - 1) 4) (made-up data) Hypothesis Test problem for TWO population DIFFERENCES (not proportions or means) comparison hypothesis test (NOT a proportion problem - so we use t-values, not z-values). SHOW t-TEST SETUP and calculation, AND for the t-Critical, what SIGNIFICANCE LEVEL (the column) and what df (which row) were used and what the t-Critical value is. Do people avoid driving on Friday the 13th ? Here are data on 20 Fridays: 10 on the 13th and the other 10 on the Friday before. For the DIFFERENCES, Calculate the MEAN and SD between traffic on these two Fridays at the 95% level (alpha = 5%); Traffic Count

TIME IT TAKES FOR TWO DIFFERENT MEDICATION TO TAKE EFFECT A B 44 79 100 Time to Effect 45 79 90 50 83 30 52 79 70 42 73 60 51 75 47 73 Minutes 250 42 79 40 40 80 30 44 85 20 47 87 10 48 81 47 72 0 2 4 6 10 12 14 16 53 75 Person # 55 74 47.1 78.3 MEAN 19.4 20.8 VARIANCE 4.4 4.6 STD DEVIATIONt-Test = [(x-bar1 - x-bar2) -((1 - (2)] / sqrt ( s121 + $232) To find the t-Critical we need the degrees of freedom (df): df = (n1 -1) + (n2 - 1) Also, find the p-value Bottom line: Is there a significant difference between the mean "time to take effect" for these two medications and if so, which medication is significantly faster. MOVING ON TO ANOVA (Analysis of Variance) We have just finished comparing the means of TWO data sets to determine if there is a significant difference between them. We have used the z-Test (proportions) and the t-Test to do this. We FINALLY find a use for the VARIANCE ! We haven't used the variance very much in this course, just its square root, the standard deviation. There is a LOT of squaring (and maybe swearing) in ANOVA calculations and if you recall from your Week 1 exercise in calculating variance, we squared distances to make any negative ones, positive. This is what we are essentially doing here, but in multiple dimensions.\fPlant 1 Plant 2 Plant 3 Plant 4 Plant 5 n Mean Variance Fill in the Table above ^\fF critical values Degrees of freedom in the numerator 3 S 3.01 2.42 2.29 2.20 2.13 2.09 2.04 2.00 4.41 3.45 3.16 2.91 2.77 2.58 2.51 2.46 3.71 DOI 65 01 8.49 7.46 5.81 6 35 6.02 5.76 2.18 211 2.012 090 3.$2 3.13 2.90 2.74 2.54 2.42 19 5.90 451 3.90 3.56 3.3.3 3.17 3.05 2.06 2.8R 0TO 5,01 4.50 417 10.16 8.24. 7.27 5.45 5.59 5.39 2.18 2.15 2.10 2.04 4.35 3.49 3.10 2.87 2.71 2.51 2.45 20 025 5.47 4.46 3.86 3.51 3.20 313 3.01 2.91 010 5.85 4.43 4.10 387 3.70 3.59 3.46 8,10 7.10 4.#4 2.14 2.21 2.14 2.01 050 4.32 3.47 3.07 2.84 2.68 2 57 2.49 2.42 2.37 21 4.42 3.62 3.48 3.25 2.97 2.87 2.80 C 010 R.OF 5.78 4.31 4.0 3.64 1.40 4.77 7.4 $11 2.95 1.46 2.35 2.21 2.01 1.97 1.93 050 2.83 3.14 22 025 5.79 438 3.22 3.05 2.93 2.84 2.76 010 7.95 5.7 4.12 4.31 3.76 3.59 3.45 3.35 14.18 6.81 1.44 4.19 Degrees of freedom in the denominator 100 2.94 2.55 2.34 2.21 2.11 205 1.95 1.92 050 4.28 3.42 2.80 2.44 2.37 2.32 1,41 010 4. TO 3.94 371 3.54 3.41 3.30 1420 2.47 7.67 6. 70 5.3.3. 5.09 2.19 2.10 2 04 3.40 3.01 2.78 2.62 251 2.42 2.35 2.310 24 5.32 3.72 3.38 3.15 2.99 2.47 2.75 2.70 010 7.82 5.61 4.72 4.22 367 3.50 14.03 934 6.59 1.80 2.53 2.32 2.18 2.04 202 1.97 1.93 1.49 050 4.24 3.39 2.59 2.76 2.60 2.49 2.40 2.34 2.28 25 .015 4.20 3.35 4.13 2.75 010 7.77 5.57 1, 17 13.48 9.22 7.45 6.49 5.85 5.15 4.31 2.91 242 2.11 2.08 1.02 I.AK