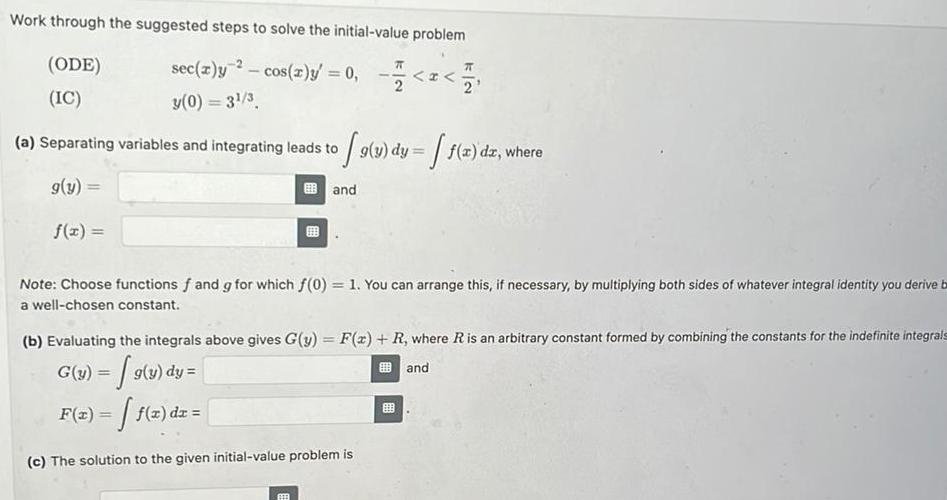
Work through the suggested steps to solve the initial-value problem (ODE) (IC) sec(z)y 2 - cos(x)y' = 0, y(0) = 31/3 < < (a) Separating variables and integrating leads to 9(y) dy = f(x) dz, where g(y)= f(x) = and Note: Choose functions f and g for which f(0) = 1. You can arrange this, if necessary, by multiplying both sides of whatever integral identity you derive b a well-chosen constant. (b) Evaluating the integrals above gives G(y) = F(x) + R, where R is an arbitrary constant formed by combining the constants for the indefinite integrals G(y) = g(y) dy = and F(x) = f(x) dx = (c) The solution to the given initial-value problem is