Question: 1) Write a function divdiff in matlab. The function should read in two vectors x and y, and returns a table (a matrix) of

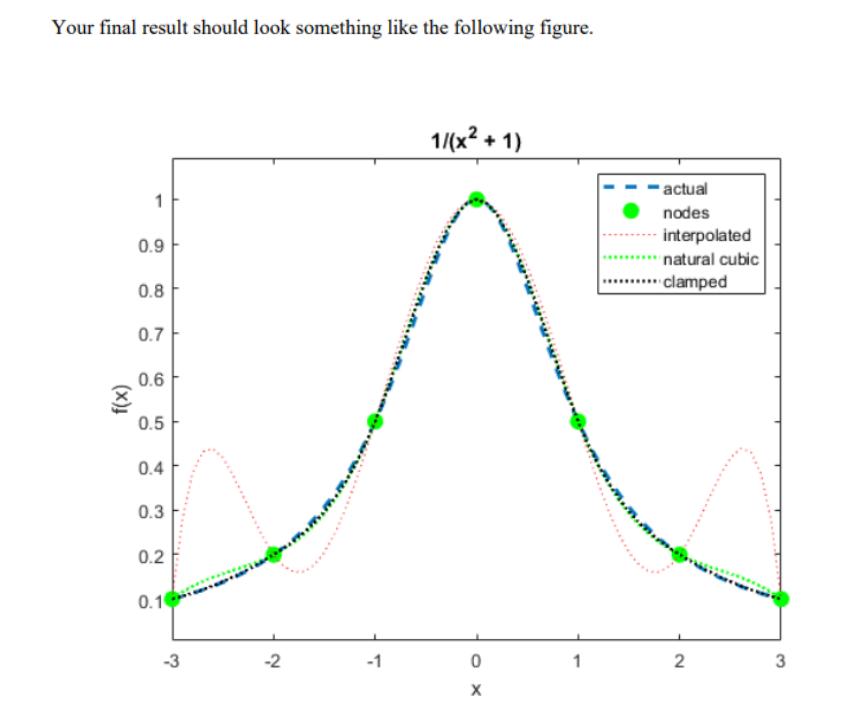

1) Write a function divdiff in matlab. The function should read in two vectors x and y, and returns a table (a matrix) of the divided difference values. The prototype of the function is: function a = divdiff(x, y) tinput: x, y: the data set to be interpolated Soutput: a: a table for Newton's divided differences 2) Write a function called polyvalue, that reads in the table of divided difference values generated by the function divdiff, the x-vector, and a vector t. The output of the function should be the values of Newton't polynomial computed at points gives in the vector t. The prototype of the polyvalue function is function v = polyvalue (a, x, t) $ input: a = Newton's divided differences x = the ponts for the dataset, same as in divdiff t = the points where the polynomial should be evaluated 3) Test your Matlab functions in a and b using 11 equally spaced nodes on the interval [-5, 5] (>> x = -5:5 ), find the interpolating polynomial p of degree 10 for the function f (x) = (x2 + 1)-1. Plot the function f(x) using the matlab ezplot function. Then on the same plot (use hold on) plot p(x) at the 11 point. Does it work well or poor? explain why? 4) Now, use the cubic spline interpolation provided by the matlab functions spline and ppval to generate the interpolation assuming natural cubic spline. Plot the result on the same plot as in three. 5) Repeat (4), but now use clamped cubic spline instead. You can do that by differentiating the function and finding f'(-.5) and f'(.5). Plot the result on the same plot as in 3 and 4. Your final result should look something like the following figure. 1/(x2 + 1) actual 1 nodes interpolated 0.9 natural cubic ....clamped 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.10 -3 -2 -1 1 3. 2. m.m.m m.m.m mimo (x), What to turn in: Submit a zip file that contains the required matlab files that would generate a figure similar to the above figure. Explain which method is the best for this problem, natural cubic spline or clamped cubic spline or Newton's divided difference. 1) Write a function divdiff in matlab. The function should read in two vectors x and y, and returns a table (a matrix) of the divided difference values. The prototype of the function is: function a = divdiff(x, y) tinput: x, y: the data set to be interpolated Soutput: a: a table for Newton's divided differences 2) Write a function called polyvalue, that reads in the table of divided difference values generated by the function divdiff, the x-vector, and a vector t. The output of the function should be the values of Newton't polynomial computed at points gives in the vector t. The prototype of the polyvalue function is function v = polyvalue (a, x, t) $ input: a = Newton's divided differences x = the ponts for the dataset, same as in divdiff t = the points where the polynomial should be evaluated 3) Test your Matlab functions in a and b using 11 equally spaced nodes on the interval [-5, 5] (>> x = -5:5 ), find the interpolating polynomial p of degree 10 for the function f (x) = (x2 + 1)-1. Plot the function f(x) using the matlab ezplot function. Then on the same plot (use hold on) plot p(x) at the 11 point. Does it work well or poor? explain why? 4) Now, use the cubic spline interpolation provided by the matlab functions spline and ppval to generate the interpolation assuming natural cubic spline. Plot the result on the same plot as in three. 5) Repeat (4), but now use clamped cubic spline instead. You can do that by differentiating the function and finding f'(-.5) and f'(.5). Plot the result on the same plot as in 3 and 4. Your final result should look something like the following figure. 1/(x2 + 1) actual 1 nodes interpolated 0.9 natural cubic ....clamped 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.10 -3 -2 -1 1 3. 2. m.m.m m.m.m mimo (x), What to turn in: Submit a zip file that contains the required matlab files that would generate a figure similar to the above figure. Explain which method is the best for this problem, natural cubic spline or clamped cubic spline or Newton's divided difference. 1) Write a function divdiff in matlab. The function should read in two vectors x and y, and returns a table (a matrix) of the divided difference values. The prototype of the function is: function a = divdiff(x, y) tinput: x, y: the data set to be interpolated Soutput: a: a table for Newton's divided differences 2) Write a function called polyvalue, that reads in the table of divided difference values generated by the function divdiff, the x-vector, and a vector t. The output of the function should be the values of Newton't polynomial computed at points gives in the vector t. The prototype of the polyvalue function is function v = polyvalue (a, x, t) $ input: a = Newton's divided differences x = the ponts for the dataset, same as in divdiff t = the points where the polynomial should be evaluated 3) Test your Matlab functions in a and b using 11 equally spaced nodes on the interval [-5, 5] (>> x = -5:5 ), find the interpolating polynomial p of degree 10 for the function f (x) = (x2 + 1)-1. Plot the function f(x) using the matlab ezplot function. Then on the same plot (use hold on) plot p(x) at the 11 point. Does it work well or poor? explain why? 4) Now, use the cubic spline interpolation provided by the matlab functions spline and ppval to generate the interpolation assuming natural cubic spline. Plot the result on the same plot as in three. 5) Repeat (4), but now use clamped cubic spline instead. You can do that by differentiating the function and finding f'(-.5) and f'(.5). Plot the result on the same plot as in 3 and 4. Your final result should look something like the following figure. 1/(x2 + 1) actual 1 nodes interpolated 0.9 natural cubic ....clamped 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.10 -3 -2 -1 1 3. 2. m.m.m m.m.m mimo (x), What to turn in: Submit a zip file that contains the required matlab files that would generate a figure similar to the above figure. Explain which method is the best for this problem, natural cubic spline or clamped cubic spline or Newton's divided difference.
Step by Step Solution
3.52 Rating (152 Votes )
There are 3 Steps involved in it
Mtlb de fr Newtn divide differene frmultin ler ll lse ll funtin fr whih interltin hve t d fx x211 ll ... View full answer

Get step-by-step solutions from verified subject matter experts


