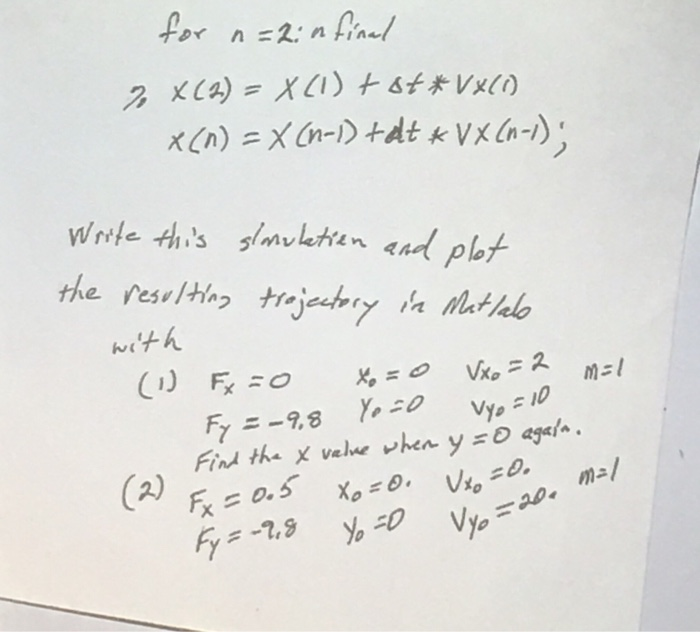Write a Matlab program (script or function or combination of both at your option) that simulates a two dimensional (x and y) trajectory of a mass, m, with a specified applied force. The state of this single mass system is given by the position and velocity: x, y, vx, vy. The core algorithm to update the state from values known at time step (n) to the next state at time step (n+1) is given by: x(n+1) = x(n) + dt * vx(n) y(n+1) = y(n) + dt* vy(n) vx(n+1) = vx(n) + dt * Ex(n)/m vy(n+1) = vy(n) + dt * Fy(n)/m Run your simulation for two sets of initial conditions and applied force: 1. Fx = 0; Fy=-9.8; x0 = 0; yO=0; vx0=2; vy0=10; m=1; For this case, find the value of x when y returns to zero. 2. Fx=0.5; Fy=-9.8; x0 = 0; yO=0; vx0 = 0; vy0 = 20; m = 1; Plot the resulting trajectory. for n=2in final 2 X(3) = x(i) +8+*VX60 x(n) = x (n-) +dt * VX (n-1); Write this slauktien and plet the resulting trajectory in Matlalo with (1) Ex=0 Xo=0 Vxo =2 m=1 Fy = -9,8 Yo=0 vyo=10 Find the x value when y=0 again. Fx = 0.5 Xo=0. Vxo =0. m=1 Fy = -9,8 Yo =0 Vy=2 Write a Matlab program (script or function or combination of both at your option) that simulates a two dimensional (x and y) trajectory of a mass, m, with a specified applied force. The state of this single mass system is given by the position and velocity: x, y, vx, vy. The core algorithm to update the state from values known at time step (n) to the next state at time step (n+1) is given by: x(n+1) = x(n) + dt * vx(n) y(n+1) = y(n) + dt* vy(n) vx(n+1) = vx(n) + dt * Ex(n)/m vy(n+1) = vy(n) + dt * Fy(n)/m Run your simulation for two sets of initial conditions and applied force: 1. Fx = 0; Fy=-9.8; x0 = 0; yO=0; vx0=2; vy0=10; m=1; For this case, find the value of x when y returns to zero. 2. Fx=0.5; Fy=-9.8; x0 = 0; yO=0; vx0 = 0; vy0 = 20; m = 1; Plot the resulting trajectory. for n=2in final 2 X(3) = x(i) +8+*VX60 x(n) = x (n-) +dt * VX (n-1); Write this slauktien and plet the resulting trajectory in Matlalo with (1) Ex=0 Xo=0 Vxo =2 m=1 Fy = -9,8 Yo=0 vyo=10 Find the x value when y=0 again. Fx = 0.5 Xo=0. Vxo =0. m=1 Fy = -9,8 Yo =0 Vy=2