Write a program in Python:

Your solution should be a neatly typed report that walks a reader through the problem presented below. Illustrate your work with plots and code. (Use python or matlab)

In class we used Taylors Theorem to create numerical methods that would approximate the derivative of a function f(x). Lets explore Taylors Theorem approximations to the derivative and second derivative for specified function. Specifically lets working on the interval from [0,2?] with the function f(x) = Asin(x) + B cos(x) where A and B are constant integers in the set {0,1}. You can now write a code that will approximate the derivative to f(x) given a discrete representation of f(x) at n points. This means you will know two vectors: xn := a collection of the n equally spaced points on the interval [0,2?]. fn := a collection of function evaluations of f(x) at the n points specified in xn.

You will be looking for the vectors f'_{n} and ?f''_{n}.

Specific Coding Tasks

You should develop a first and second order method for approximating the first derivative, and a second order method for approximating the second derivative using Taylors Theorem (You have seen this in class). You should then test your approximation using all permutations of the coefficients A and B using a mesh or grid refinement and exploring the error obtained. I outline this below.

Assumptions that can be made:

Lets assume you know the derivative and second derivative at the endpoints exactly (you can compute these values by hand). If xn[0] = 0, and xn[n] = 2? then this means that f'_{n}[0], f'_{n}[n], f''_{n}[0] and f''_{n}[n] are all known values. The other values should all be computed using your Taylors Theorem approximations. Grid Refinement A grid refinement or mesh refinement is done by looking at the error when more points are used. To conduct a grid refinement look at the error in your approximation when n = 10,20,40,80,160,320 points are used. The error in the approximation of the derivative should be found using the following expression where g represents the true derivative of f.

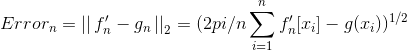
You can extend this definition for the second derivative grid refinement study.

Order of Convergence

Note that you can solve the following relation for the value of ?:

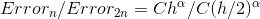
As you do your mesh refinement you should see ? approach a fixed value. Make a table for the values of ? you see in your numerical experiments. It will look like the following:

A = 0,B = 0 A = 1,B = 0 A = 0,B = 1 A = 1,B = 1

first order f0 NA ?? ?? ??

second order f0 NA ?? ?? ??

second order f00 NA ?? ?? ??

where the values in the table represent the order of convergence you have achieved. Note that I have placed a value of NA in the chart for the A = 0,B = 0 case as this is trivial and boring.

Why do you think you see the values in the table that you do? (Hint: Note the Taylors Theorem expansion of even and odd functions may help you answer this question.) I will be looking for the following:

Three Taylors Theorem approximations functions that take a vector and give back a vector.

Function used for the true derivative, and a function used for the true second derivative.

Functions that looks at the error of your approximations.

The grid refinement study.

Some illustrating plots.

Analysis where appropriate.

Error, _ gn lla (2pi> f, -g(zi) ) 1/2 Errorn = 11 J n