Write acomplete Java program to implement Quick and Merge sortingalgorithms.

Input an arrayof double data type, and choice of sorting algorithm to be used,from the user.

Display thesorted array to the user.

Runthe program and display output samples [2Marks]

(Hint Refer toLab 9)

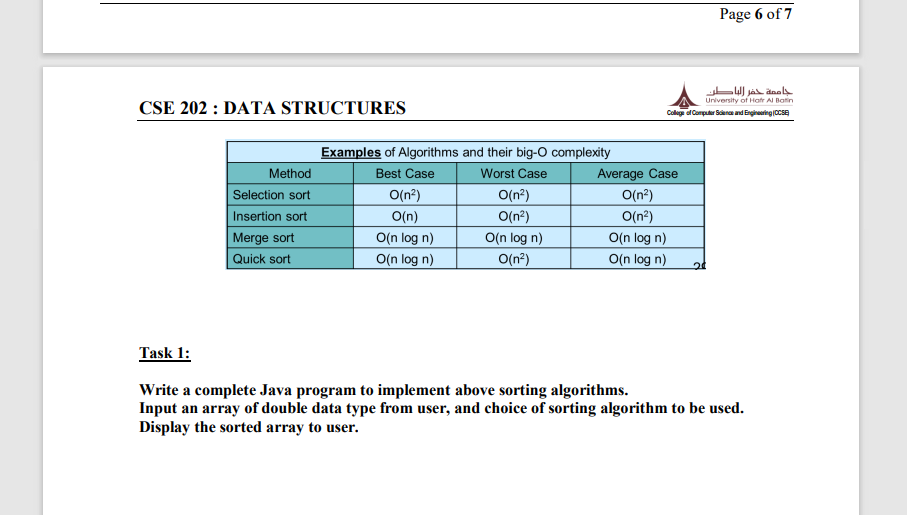
LAB 09: Recursion Objectives: To implement some of the recursive algorithms and analyze their complexity. 1. Recursion We have seen so far that a function, such as main, can call another function to perform some computation. In Java, a function can also call itself. Such types of functions are called recursive functions. A function, f, is also said to be recursive if it calls another function, g, which in turn calls f. Although it may sound strange for a function to call itself, it is in fact not so strange, as many mathematical functions are defined recursively... e.g., factorial function: n! = Although less efficient than iterative functions (using loops) due to overhead in function calls, in many cases, recursive functions provide a more natural and simple solutions. Thus, recursion is a powerful tool in problem solving and programming. Problems that can be solved using recursion have the following characteristics: One or more simple cases of the problem have a direct and easy answer - also called base cases. Example: 0! = 1. The other cases can be re-defined in terms of a similar but smaller problem - recursive cases. Example: n! =n(n-1)! By applying this re-definition process, each time the recursive cases will move closer and eventually reach the base case. Example: n! (n-1)! (n-2)! ... 1!, 0!. The strategy in recursive solutions is called divide-and-conquer. The idea is to keep reducing the problem size until it reduces to the simple case with obvious solution. size n problem } Recursive version int factorial (int n) { if n = 0, n* (n-1)! if n>0 if (n == 0) return 1; size n-1 problem size 1 problem //base case Example: Recursive Factorial The following code shows the recursive and iterative versions of the factorial function: //recursive case else return n*factorial (n-1); size n-2 problem size 1 problem } Iterative version int factorial (int n) { size 2 problem size 1 problem size 1 problem int i, product=1; for (i=n; i>1; -1) product=product * i; return product; size 1 problem In recursive functions such as above: The if branch is the base case, while the else branch is the recursive case. For the recursion to terminate, the recursive case must be moving closer to the base case. Tracing the Recursive Functions Executing recursive algorithms goes through two phases: Expansion in which the recursive step is applied until hitting the base step. factorial(4) = 4* factorial (3) = 4*(3* factorial (2)) = 4*(3* (2* factorial (1))) The following diagram from wikipedia shows the complete merge sort process for an example array (38, 27, 43, 3, 9, 82, 10}. If we take a closer look at the diagram, we can see that the array is recursively divided in two halves till the size becomes 1. Once the size becomes 1, the merge processes comes into action and starts merging arrays back till the complete array is merged. = 4*(3* (2*(1 * factorial (0)))) = 4*(3* (2 (11))) = 4*(3* (2*1)) 38 = 4*(3*2) = 4*6 = 24 CSE 202: DATA STRUCTURES Substitution in which the solution is constructed backwards starting with the base step. 2. Sorting Algorithms Call mergeSort (arr, m+1, r) 4. Merge the two halves sorted in step 2 and 3: Call merge (arr, 1, m, r) 38 27 Sorting algorithms rearrange the data in some order (ascending or descending order). Following are the two very common recursive algorithms for sorting. These numbers, indicate the order steps are prohich 27 i. Merge Sort Like QuickSort, Merge Sort is a Divide and Conquer algorithm. It divides input array in two halves, calls itself for the two halves and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, 1, m, r) is key process that assumes that arr[1..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one. See following C implementation for details. MergeSort (arr [], 1, r) If r > 1 1. Find the middle point to divide the array into two halves: middle m = (1+r)/2 2. Call merge Sort for first half: Call mergeSort (arr, 1, m) 3. Call mergeSort for second half: 27 Expansion phase 38 27 43 2 Substitution phase 8 10 University of Hafr Al Batin College of Computer Science and Engineering (CCSE 38 27 43 39 82 10 27 30 9 982 10 12 02 9 82 16 9 10 82 19 82 15 7 10 27 30 43 02 20 10 10 10 18 17 Exercise # 1: Edit, compile and run the following code in Eclipse. /* Java program for Merge Sort */ public class MergeSort { 12 13. 14. 15. 16. 17. 34. 35. 36. 57. 37 50. 38. CSE 202: DATA STRUCTURES 59. 40. 40. 41. 42. Merges two of arr[]. 47. 48. // First subarray is void merge(int arr[], int 1, int m, int r) { // Find sizes of two subarrays to be merged int n1 = m - 1 + 1; int n2 = rm; /* Create temp arrays */ int L[] = new int [n1]; int R[] = new int [n2]; /*Copy data to temp arrays*/ for (int i=0; i 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71. 72. 73. 74. 75. 76. 77. 78. 79. 80. 81. 82. 83. 84. 85. 86. 87. 88. 89. 90. 91. 92. 93. 94. 95. } } /* Copy remaining elements of R[] if any */ while (j < n2) { arr[k] = R[j]; } } // Main function that sorts arr[1..r] using merge() void sort(int arr[], int 1, int r) { if (1 85. 86. 87. 88. 89. 90. 91. 92. 93. 94. } 95. } 96. /* contributed by Rajat Mishra: https://www.geeksforgeeks.org/merge-sort/ */ System.out.println( Given Array ); printArray(arr); MergeSort ob = new MergeSort(); ob.sort (arr, 0, arr.length-1); System.out.println( Sorted array ); printArray(arr); Given Array 12 11 13 5 6 7 Sorted array 567 11 12 13 ii. Quick Sort Like Merge Sort, QuickSort is a Divide and Conquer algorithm. It picks an element as pivot and partitions the given array around the picked pivot. There are many different versions of quickSort that pick pivot in different ways. 1. Always pick first element as pivot. 2. Always pick last element as pivot (implemented below) 3. Pick a random element as pivot. 4. Pick median as pivot. The key process in quickSort is partition(). Target of partitions is, given an array and an element x of array as pivot, put x at its correct position in sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x. All this should be done in linear time. Page 4 of 7 /* low --> Starting index, high --> Ending index */ quickSort (arr [], low, high) { if (low high) { to Partition Algorithm: There can be many ways do partition, following pseudo code adopts the method given in CLRS book (Introduction to Algorithms by Cormen et. al.). The logic is simple, we start from the leftmost element and keep track of index of smaller (or equal to) elements as i. While traversing, if we find a smaller element, we swap current element with arr[i]. Otherwise we ignore current element. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. } 15. 16. /* pi is partitioning index, arr [pil is now at right place */ pi partition (arr, low, high); 1. 2. public class QuickSort 3. { 4. 17. 18. 19. 20. quickSort (arr, low, pi 1); // Before pi quickSort (arr, pi + 1, high); // After pi 21. 22. 23. 24. Exercise # 2: Edit, compile and run the following code in Eclipse. Java program for implementation of QuickSort {10, 30, 40, (50) Partition around 50 {10, 30, 40} Partition around 40 (10, (30) Partition {10} around 30 { (10, 80, 30, 90, 40, 50, (70) Partition around 70 (Last element) = for (int j-low; j CSE 202: DATA STRUCTURES 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. iii. arr[high] = temp; return i+1; } /* The main function that implements QuickSort() arr[] > Array to be sorted, low --> Starting index, high > Ending index */ void sort(int arr[], int low, int high) { if (low high) { } } /* pi is partitioning index, arr[pi] is now at right place */ int pi= partition (arr, low, high); // Recursively sort elements before // partition and after partition sort(arr, low, pi-1); sort (arr, pi+1, high); /* A utility function to print array of size n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i CSE 202: DATA STRUCTURES Method Selection sort Insertion sort Merge sort Quick sort Examples of Algorithms and their big-O complexity Best Case Worst Case O(n) O(n) O(n log n) O(n log n) O(n) O(n) O(n log n) O(n) Page 6 of 7 Average Case O(n) O(n) O(n log n) O(n log n) University of Hofr Al Batin College of Computer Science and Engineering (CCSE Task 1: Write a complete Java program to implement above sorting algorithms. Input an array of double data type from user, and choice of sorting algorithm to be used. Display the sorted array to user.