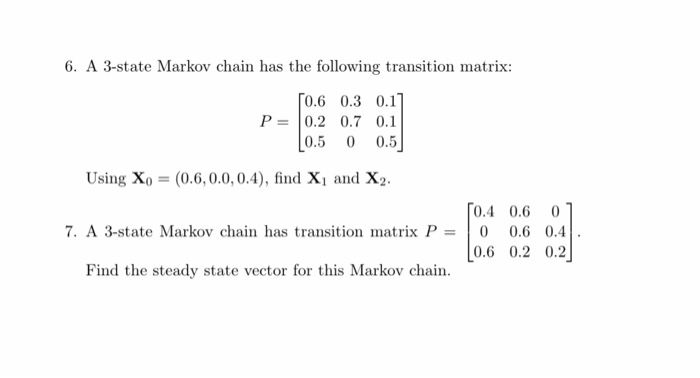
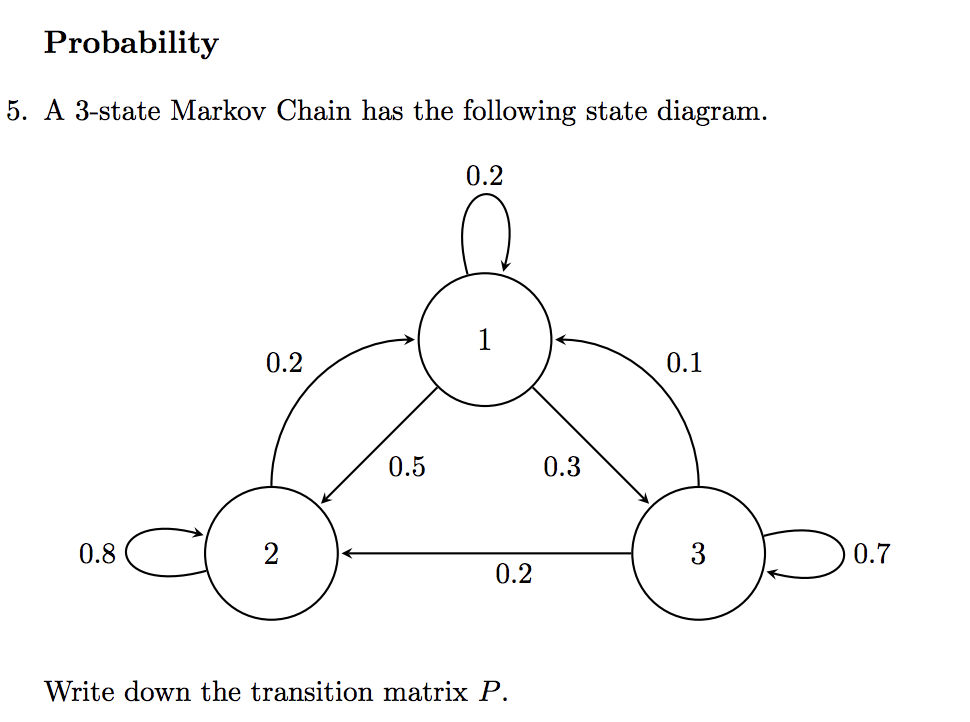
Write down the trnansition matrix
For the following word problems state if the problem requires using the Central Limit theorem or if does Not require using the Central limit theorem Circle the correct choice: 1. What is the probability of randomly selecting an adult with an IQ score less than 75? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 2. If 30 cell phones are randomly selected what is the probability the cell phones will last an average of more than 23.8 months? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 3. In general Marine platoons are around 50 strong, if a sample of a given platoon is taken from a populati of Marines with a mean weight of 200 pounds and with standard deviation o = 10. What is the probabil that the sample mean weight will be less than 196 pounds? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 4. The mean age of baseball players is 27 years. Assuming the age of baseball players are normally distributed and that the average size of a baseball team is 25 players, what is the probability a basebal player is older than 30 years if the player is randomly selected. A. Requires the Central limit theorem. B. Does not require the central limit theorem. 5. Suppose that you have a sample of 81 students from a population with mean u = 500 and with standard deviation o = 108. What is the probability that the sample mean will be greater than 483. A. Requires the Central limit theorem. B. Does not require the central limit theorem.Problem 1: A Central Limit Theorem Simulation Here we will perform a Central Limit Theorem simulation similar to the ones done in class. That is: . Pick a distribution (that was not presented in class) . Justify that the distribution will abide by the central limit theorem . Find a parameter set and value for / where we can see that the central limit theorem clearly applies . Find a parameter set and value for / where we can see that the central limit theorem does not apply . Code must be submitted (preferably in R, but MATLAB, Python, ForTran, and C++ will also be accepted).6. A 3-state Markov chain has the following transition matrix: 0.6 0.3 0.17 P = 0.2 0.7 0.1 0.5 0 0.5 Using Xo = (0.6, 0.0, 0.4), find X1 and X2. 0.4 0.6 07 7. A 3-state Markov chain has transition matrix P = 0 0.6 0.4 0.6 0.2 0.2 Find the steady state vector for this Markov chain.Probability 5. A 3-state Markov Chain has the following state diagram. 0.2 0.2 0.1 0.5 0.3 0.8 N 0.7 0.2 Write down the transition matrix P.6. A 3-state Markov chain has the following transition matrix: 0.6 0.3 0.17 P = 0.2 0.7 0.1 0.5 0 0.5 Using Xo = (0.6, 0.0, 0.4), find X1 and X2