Write the code for the count(item) and items () methods in Python 3.7 language:

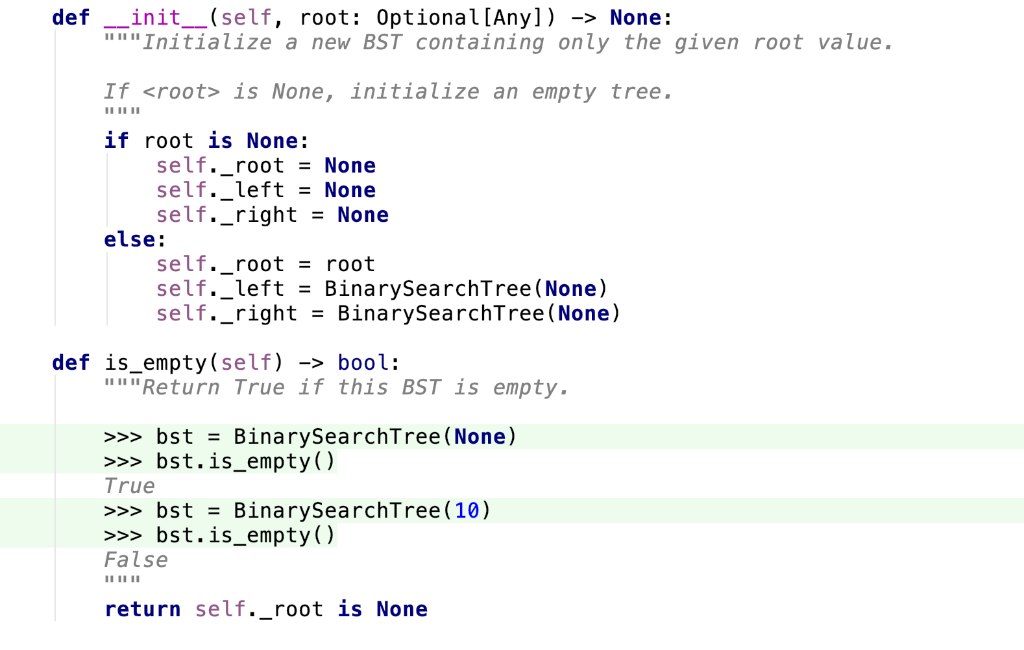
def init__(self, root: Optional [Any]) None: """Initialize a new BST containing only the given root value. If is None, initialize an empty tree if root is None: self. root - None self. left - None self._right - None else: self._root - root self._left-BinarySearchTree (None) self._right - BinarySearchTree (None) def is_empty (self) - bool: ""Return True if this BST is empty. 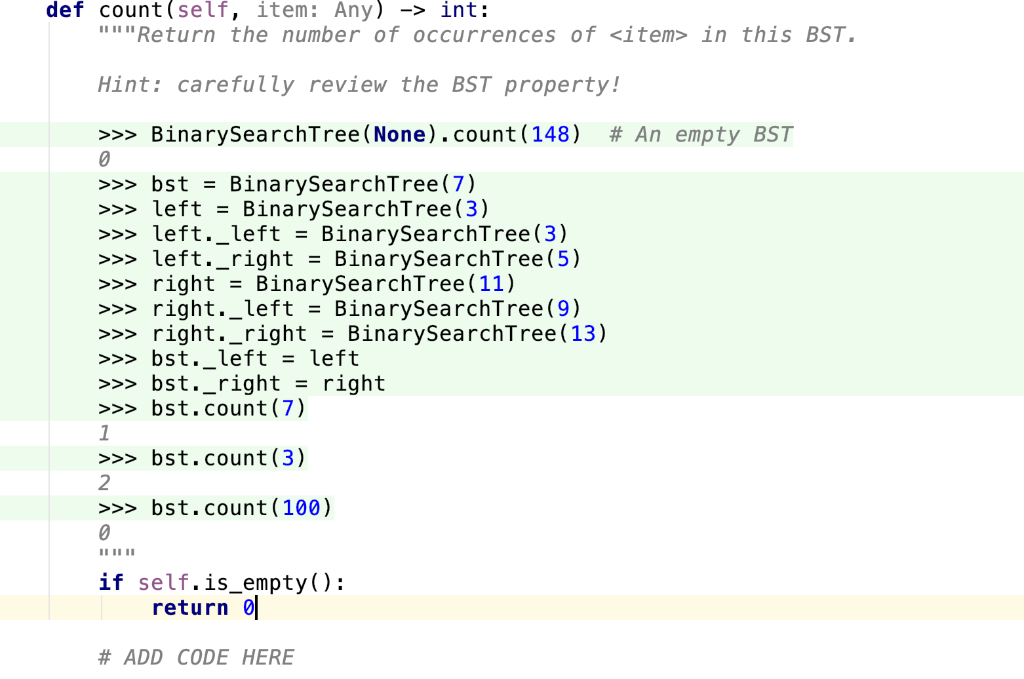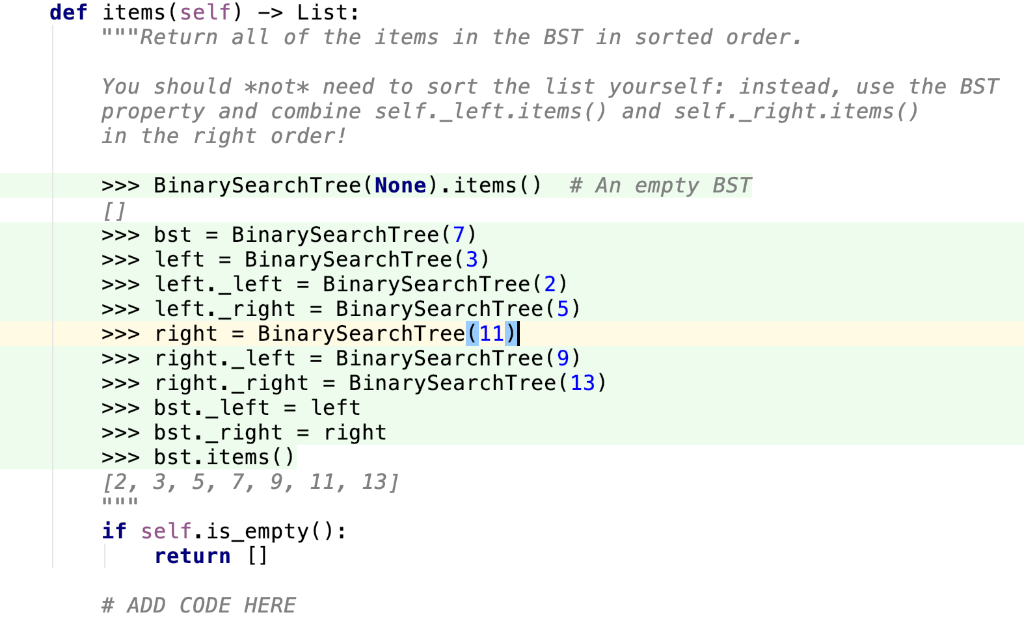>>> bst- BinarySearchTree (None) >>>bst.is_empty() True >>> bstBinarySearchTree (10) >>bst.is_empty() False return self._root is None def count(self, item: Any) ->int: Return the number of occurrences of in this BST. Hint: carefully review the BST property >>> Bina rySearchTree ( None). pty BST count (148) #Anem >bst BinarySearchTree(7) >leftBinarySearchTree(3) >left._leftBinarySearchTree (3) >>left._right - BinarySearchTree (5) >>>right BinarySearchTree (11) >>>right._left-BinarySearchTree(9) >>>right._right -BinarySearchTree (13) >bst._left -left >>>bst._right -right >bst.count (7) >bst.count (3) 2 >>>bst.count (100) if self.is_ empty (): return # ADD CODE HERE def items (self) ->List: Return all of the items in the BST in sorted order. You should *not* need to sort the list yourself: instead, use the BST property and combine self._left.items) and self._right.items () in the right order! >>> BinarySearchTree ( None). items() # An empty BST [ j >>> bst- BinarySearchTree(7) >>leftBinarySearchTree (3) >>left._left -BinarySearchTree(2) >>left._right-BinarySearchTree(5) >>>right-BinarySearchTree(11) >>>right._left-BinarySearchTree(9) >>> right._rightBinarySearchTree (13) >>bst._left-left >>>bst._right- right >>>bst.items) [2, 3, 5, 7, 9, 11, 13] if self.is_empty) return [] # ADD CODE HERE def init__(self, root: Optional [Any]) None: """Initialize a new BST containing only the given root value. If is None, initialize an empty tree if root is None: self. root - None self. left - None self._right - None else: self._root - root self._left-BinarySearchTree (None) self._right - BinarySearchTree (None) def is_empty (self) - bool: ""Return True if this BST is empty. >>> bst- BinarySearchTree (None) >>>bst.is_empty() True >>> bstBinarySearchTree (10) >>bst.is_empty() False return self._root is None def count(self, item: Any) ->int: Return the number of occurrences of in this BST. Hint: carefully review the BST property >>> Bina rySearchTree ( None). pty BST count (148) #Anem >bst BinarySearchTree(7) >leftBinarySearchTree(3) >left._leftBinarySearchTree (3) >>left._right - BinarySearchTree (5) >>>right BinarySearchTree (11) >>>right._left-BinarySearchTree(9) >>>right._right -BinarySearchTree (13) >bst._left -left >>>bst._right -right >bst.count (7) >bst.count (3) 2 >>>bst.count (100) if self.is_ empty (): return # ADD CODE HERE def items (self) ->List: Return all of the items in the BST in sorted order. You should *not* need to sort the list yourself: instead, use the BST property and combine self._left.items) and self._right.items () in the right order! >>> BinarySearchTree ( None). items() # An empty BST [ j >>> bst- BinarySearchTree(7) >>leftBinarySearchTree (3) >>left._left -BinarySearchTree(2) >>left._right-BinarySearchTree(5) >>>right-BinarySearchTree(11) >>>right._left-BinarySearchTree(9) >>> right._rightBinarySearchTree (13) >>bst._left-left >>>bst._right- right >>>bst.items) [2, 3, 5, 7, 9, 11, 13] if self.is_empty) return [] # ADD CODE HERE