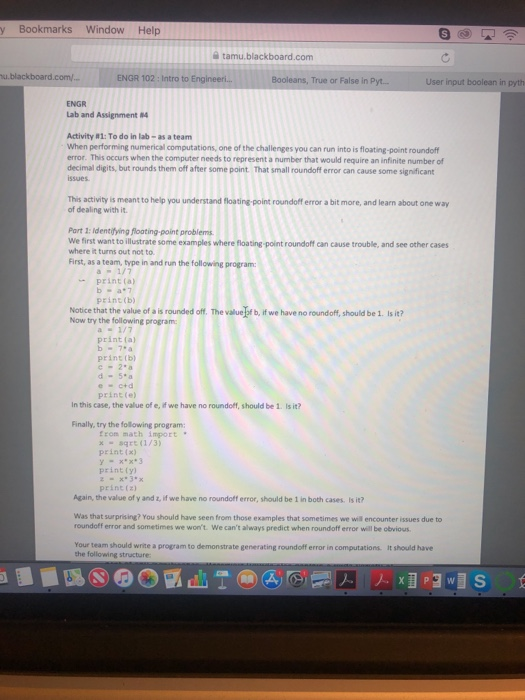
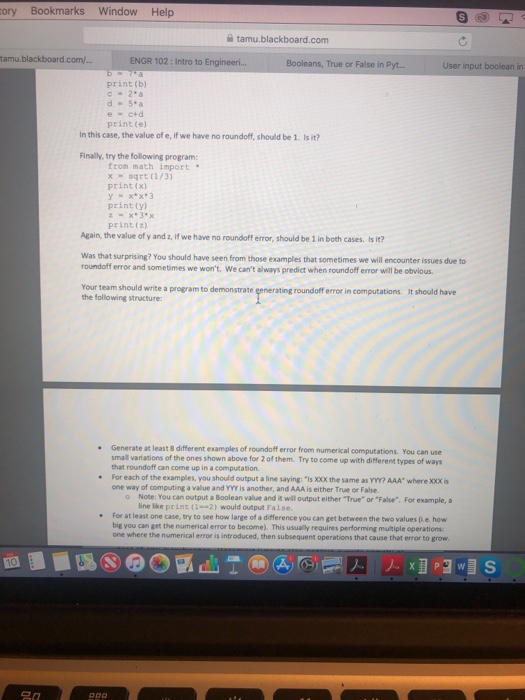
y Bookmarks Window Help e tamu. blackboard.com blackboard.com/. E ENGR 102: Intro to Engineeri.. . Booleans, True or False in Pyt. User input boolean in pyth ENGR Lab and Assignment #4 Activity #1: To do in lab- as a team When performing numerical computations, one of the challenges you can run into is floating-point roundoff error. This occurs when the computer needs to represent a number that would require an infinite number of decimal digits, but rounds them off after some point. That small roundoff error can cause some significant issues This activity is meant to help you understand floating-point roundoff error a bit more, and learn about one way of dealing with it Part 1: Identifying floating-paint probl We first want to illustrate some examples where floating-point roundoff can cause trouble, and see other cases where it turns out not to. First, as a team, type in and run the following pr print (a) print(b) Notice that the value of a is rounded off. The valueo b, if we have no roundoff, should be 1. Is it? Now try the following program print (a) print (b) c-2.a print(el In this case, the vallue of e, if we have no roundoff, should be 1. Is it? Finally, try the following program: from math import . peint(x) print(y print(z) Again, the value of y and z, if we have no roundoff error, should be 1 in both cases. Is it? Was that surprising? You should have seen from those examples that sometimes we will encounter issues due to roundoff error and sometimes we won't We can't always predict when roundoff error will be obvious Your team should write a program to demonstrate generating roundoff error in computations. the following stracture It should have tory Bookmarks Window Helo tamu.blackboard.com tamu. ENGR 102: Intro to Engineeri... Booleans, True or False in Pyt. User input boolean in print (b) c2*a d-5*a ec+d print(e) In this case, the value of e, if we have no roundoff, should be 1. Is it? Finally, try the following program from math import * xsqrt (1/3) print(x) xx*3 print (yl print (z) Again, the value of y and z, if we have no roundoff error, should be 1 in both cases. Is it? Was that surprising? You should have seen from those examples that sometimes we will encounter issues due to error and sometimes we won't. We can't always predict when roundoff error will be obvious Your team should write a program to demonstrate the following structure roundoff error in computations. It should have Generate at least 8 different examples of roundoff error from numerical computations. You can use small variations of the ones shown above for 2 of them. Try to come up with different types of ways that roundoff can come up in a computation e For each of the examples, you should output a line saying: "ls X00X the same as YYY? AAA" where XXX is one way of computing a value and YYY is another, and AAA is either True or False. o Note: You can output a Boolean value and it will output either "True" or "False". For example,a line Ike print (1- 2) would output False For at least one case, try to see how large of a difference you can get between the two values (ie. how big you can get the numerical error to become). This usually requires performing multiple operations one where the numerical error is introduced, then subsequent operations that cause that error to grow