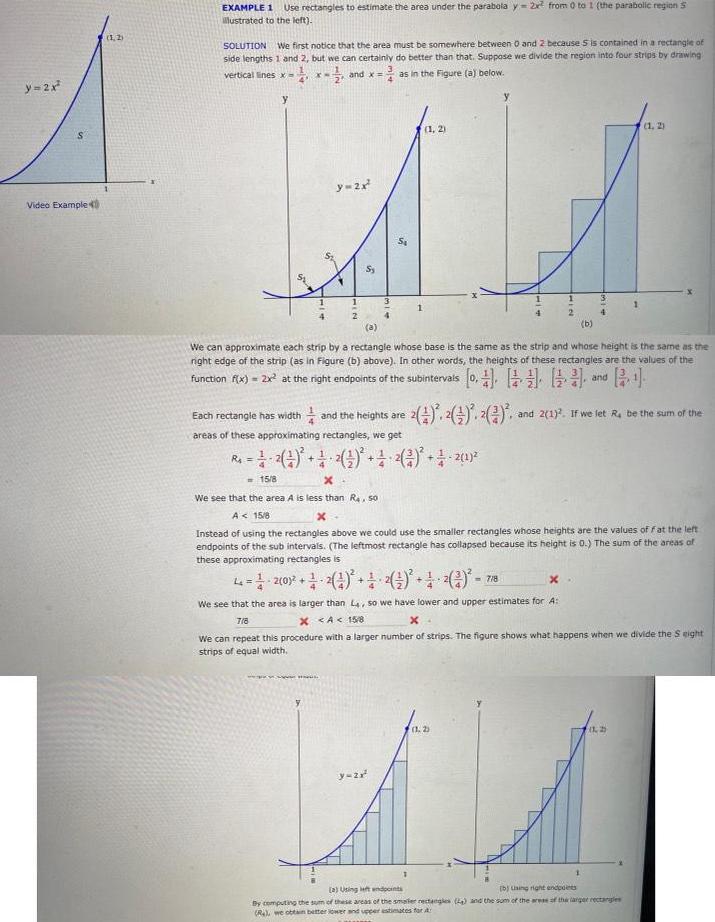
y=2x Video Example (1,2) EXAMPLE 1 Use rectangles to estimate the area under the parabola y 2x from 0 to 1 (the parabolic region 5 illustrated to the left). SOLUTION We first notice that the area must be somewhere between 0 and 2 because S is contained in a rectangle of side lengths 1 and 2, but we can certainly do better than that. Suppose we divide the region into four strips by drawing vertical lines x= as in the Figure (a) below. y and x = y=2x S 5 S 1 3 1 (a) (1, 2) I 1 3 2 4 (b) (1, 2) We can approximate each strip by a rectangle whose base is the same as the strip and whose height is the same as the right edge of the strip (as in Figure (b) above). In other words, the heights of these rectangles are the values of the and function f(x)=2x2 at the right endpoints of the subintervals Pand Each rectangle has width and the heights are areas of these approximating rectangles, we get =2(4). 2(+). (*). and 2(1). If we let R, be the sum of the *+2() ++(1)+2(1)+1.2(1) R = 15/8 x We see that the area A is less than R., so A 15/8 x Instead of using the rectangles above we could use the smaller rectangles whose heights are the values of fat the left endpoints of the sub intervals. (The leftmost rectangle has collapsed because its height is 0.) The sum of the areas of these approximating rectangles is =2(0)+2() + 2() + 2(2) - -7/8 x We see that the area is larger than L, so we have lower and upper estimates for A: 7/8 X