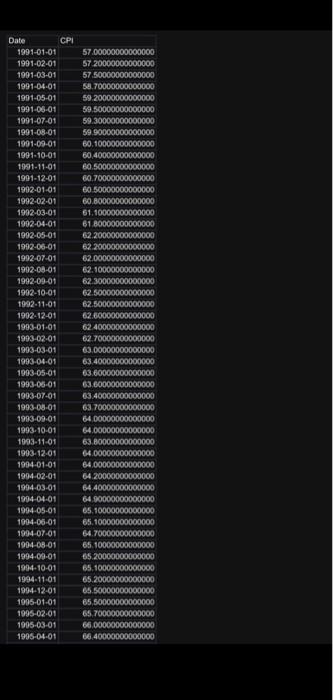
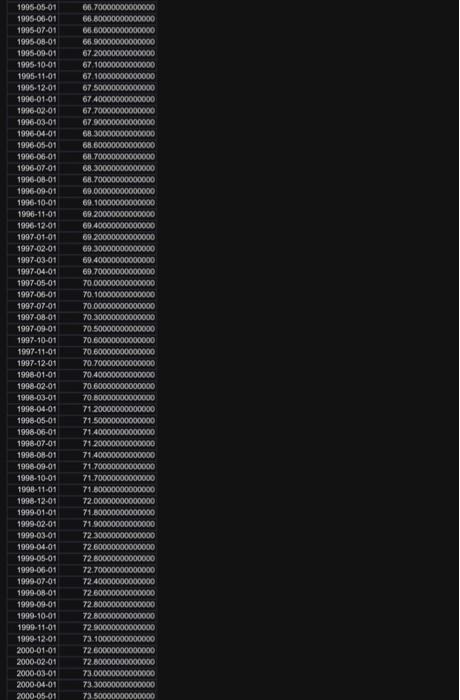
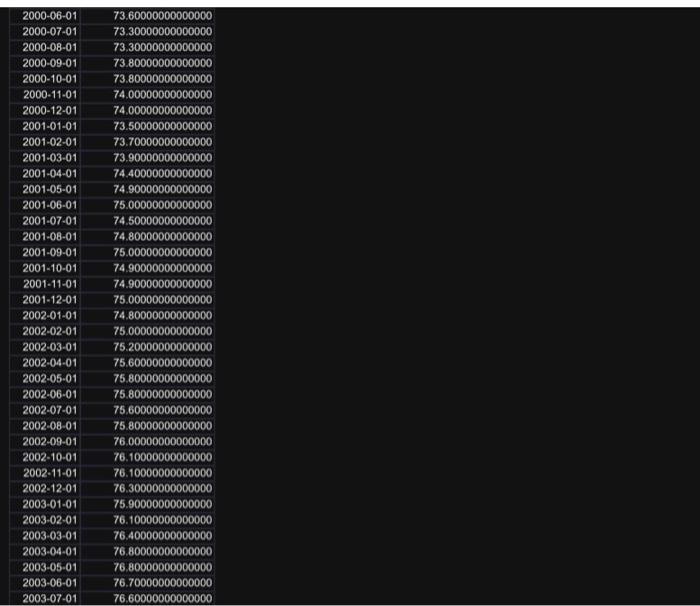
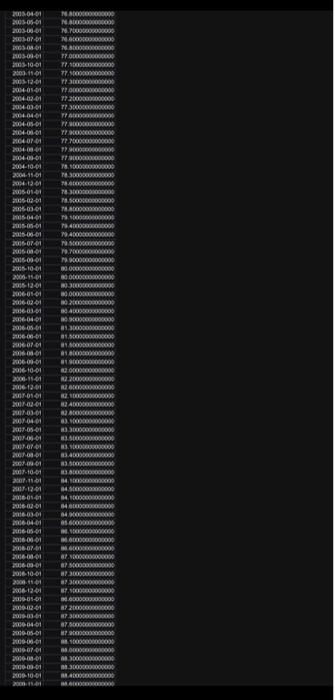
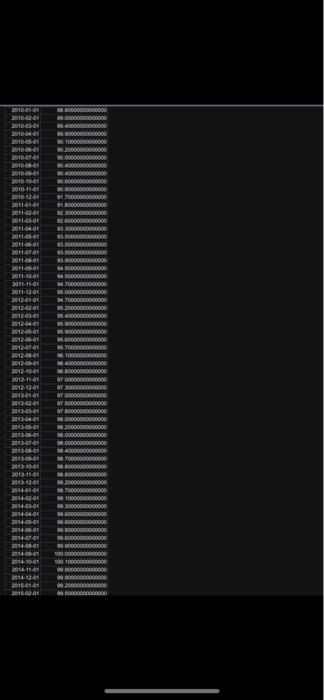
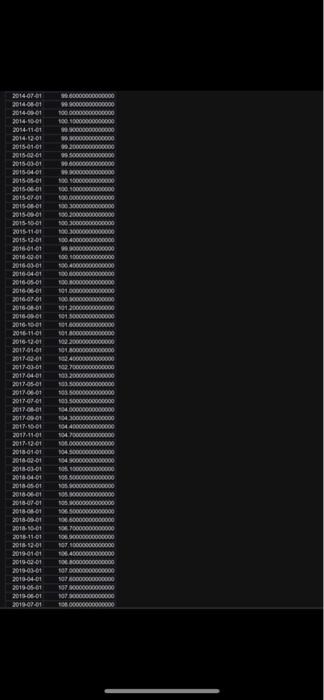
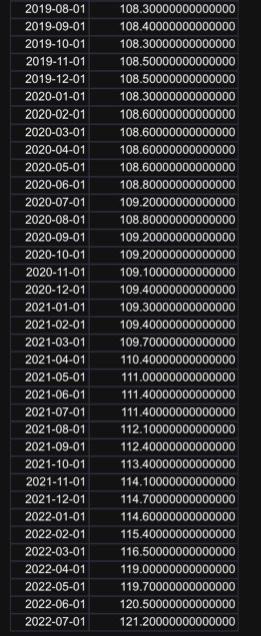
You are given monthly data of the U.K. Consumer Price Index (CPI) over the period 1991M1 to 2022M7. The data file name is "CPI.xls", uploaded alongside this file (photos). First calculate the UK inflation rate, i.e., cpit= cpit -cpit-1, where cpit is the natural logarithm of the CPI at time t and is the first difference operator. Then:

a) Explain the Box-Jenkins approach in building an ARMA(p,q) model for cpit.

b) Use the full sample period to obtain a graph of the cpit series. Based on the graph, does the series appear to be stationary? Comment on the behaviour of this series over time.

c) Explain the terms autocorrelation function (ACF) and partial autocorrelation function (PACF). What shape would these two functions take for a stationary autoregressive process, a moving average process, and an autoregressive moving average process?

d) Obtain the autocorrelation function (ACF) and partial autocorrelation function (PACF) for the cpit series (specify the number of lags to be 6) using data from 1991M1 to 2020M12 (Note that this is not the full sample). Discuss the significance of the ACF and PACF coefficients and identify the suitable models that you would estimate.

e) Estimate all ARMA models from order (0, 0) to (6, 6) for the cpit series over the shorter sample period 1991M1 to 2020M12. From your estimations, which is the suitable model order? Explain why? (You would also need to report all relevant information for the models that you estimate, including the value of the AIC and SBIC and other relevant required criteria in a Table).

f) Re-estimate only the suitable model(s) identified from Question (e). Again, use only the sample 1991M1 to 2020M12. Report and comment on the results. Perform diagnostic checks on the residuals from these estimated model(s). Do the model(s) fit the data well?

g) Use the model(s) estimated in Question (f) to generate one step ahead (static) forecasts for the period 2021M1 2022M7. Create a graph of the actual cpit series and the forecasts that you have generated over the specified out-of-sample period. Comment on the results.

Conduct all your statistical tests at the 5% level.

\begin{tabular}{|c|c|} \hline 20000601 & 73.60000000000000 \\ \hline 20000701 & 73.30000000000000 \\ \hline 20000801 & 73.30000000000000 \\ \hline 20000901 & 73.80000000000000 \\ \hline 20001001 & 73.80000000000000 \\ \hline 20001101 & 74.00000000000000 \\ \hline 20001201 & 74.00000000000000 \\ \hline 20010101 & 73.50000000000000 \\ \hline 20010201 & 73.70000000000000 \\ \hline 20010301 & 73.90000000000000 \\ \hline 20010401 & 74.40000000000000 \\ \hline 20010501 & 74.90000000000000 \\ \hline 20010601 & 75.00000000000000 \\ \hline 20010701 & 74.50000000000000 \\ \hline 20010801 & 74.80000000000000 \\ \hline 20010901 & 75.00000000000000 \\ \hline 20011001 & 74.90000000000000 \\ \hline 20011101 & 74.90000000000000 \\ \hline 20011201 & 75.00000000000000 \\ \hline 20020101 & 74.80000000000000 \\ \hline 20020201 & 75.00000000000000 \\ \hline 20020301 & 75.20000000000000 \\ \hline 20020401 & 75.60000000000000 \\ \hline 20020501 & 75.80000000000000 \\ \hline 20020601 & 75.80000000000000 \\ \hline 20020701 & 75.60000000000000 \\ \hline 20020801 & 75.80000000000000 \\ \hline 20020901 & 76.00000000000000 \\ \hline 20021001 & 76.10000000000000 \\ \hline 20021101 & 76.10000000000000 \\ \hline 20021201 & 76.30000000000000 \\ \hline 20030101 & 75.90000000000000 \\ \hline 20030201 & 76.10000000000000 \\ \hline 20030301 & 76.40000000000000 \\ \hline 20030401 & 76.80000000000000 \\ \hline 20030501 & 76.80000000000000 \\ \hline 20030601 & 76.70000000000000 \\ \hline 20030701 & 76.60000000000000 \\ \hline \end{tabular} \begin{tabular}{|r|r|} \hline 20190801 & 108.30000000000000 \\ \hline 20190901 & 108.40000000000000 \\ \hline 20191001 & 108.30000000000000 \\ \hline 20191101 & 108.50000000000000 \\ \hline 20191201 & 108.50000000000000 \\ \hline 20200101 & 108.30000000000000 \\ \hline 20200201 & 108.60000000000000 \\ \hline 20200301 & 108.60000000000000 \\ \hline 20200401 & 108.60000000000000 \\ \hline 20200501 & 108.60000000000000 \\ \hline 20200601 & 108.80000000000000 \\ \hline 20200701 & 109.20000000000000 \\ \hline 20200801 & 108.80000000000000 \\ \hline 20200901 & 109.20000000000000 \\ \hline 20201001 & 109.20000000000000 \\ \hline 20201101 & 109.10000000000000 \\ \hline 20201201 & 109.40000000000000 \\ \hline 20210101 & 109.30000000000000 \\ \hline 20210201 & 109.40000000000000 \\ \hline 20210301 & 109.70000000000000 \\ \hline 20210401 & 110.40000000000000 \\ \hline 20210501 & 111.00000000000000 \\ \hline 20210601 & 111.40000000000000 \\ \hline 20210701 & 111.40000000000000 \\ \hline 20210801 & 112.10000000000000 \\ \hline 20210901 & 112.40000000000000 \\ \hline 20211001 & 113.40000000000000 \\ \hline 20211101 & 114.10000000000000 \\ \hline 20211201 & 114.70000000000000 \\ \hline 20220101 & 114.60000000000000 \\ \hline 20220201 & 115.40000000000000 \\ \hline 2020301 & 116.50000000000000 \\ \hline 20201 & 119.00000000000000 \\ \hline 2001 & 119.70000000000000 \\ \hline \hline - & 120.50000000000000 \\ \hline 201 & 121.20000000000000 \\ \hline \end{tabular} \begin{tabular}{|c|c|} \hline 20000601 & 73.60000000000000 \\ \hline 20000701 & 73.30000000000000 \\ \hline 20000801 & 73.30000000000000 \\ \hline 20000901 & 73.80000000000000 \\ \hline 20001001 & 73.80000000000000 \\ \hline 20001101 & 74.00000000000000 \\ \hline 20001201 & 74.00000000000000 \\ \hline 20010101 & 73.50000000000000 \\ \hline 20010201 & 73.70000000000000 \\ \hline 20010301 & 73.90000000000000 \\ \hline 20010401 & 74.40000000000000 \\ \hline 20010501 & 74.90000000000000 \\ \hline 20010601 & 75.00000000000000 \\ \hline 20010701 & 74.50000000000000 \\ \hline 20010801 & 74.80000000000000 \\ \hline 20010901 & 75.00000000000000 \\ \hline 20011001 & 74.90000000000000 \\ \hline 20011101 & 74.90000000000000 \\ \hline 20011201 & 75.00000000000000 \\ \hline 20020101 & 74.80000000000000 \\ \hline 20020201 & 75.00000000000000 \\ \hline 20020301 & 75.20000000000000 \\ \hline 20020401 & 75.60000000000000 \\ \hline 20020501 & 75.80000000000000 \\ \hline 20020601 & 75.80000000000000 \\ \hline 20020701 & 75.60000000000000 \\ \hline 20020801 & 75.80000000000000 \\ \hline 20020901 & 76.00000000000000 \\ \hline 20021001 & 76.10000000000000 \\ \hline 20021101 & 76.10000000000000 \\ \hline 20021201 & 76.30000000000000 \\ \hline 20030101 & 75.90000000000000 \\ \hline 20030201 & 76.10000000000000 \\ \hline 20030301 & 76.40000000000000 \\ \hline 20030401 & 76.80000000000000 \\ \hline 20030501 & 76.80000000000000 \\ \hline 20030601 & 76.70000000000000 \\ \hline 20030701 & 76.60000000000000 \\ \hline \end{tabular} \begin{tabular}{|r|r|} \hline 20190801 & 108.30000000000000 \\ \hline 20190901 & 108.40000000000000 \\ \hline 20191001 & 108.30000000000000 \\ \hline 20191101 & 108.50000000000000 \\ \hline 20191201 & 108.50000000000000 \\ \hline 20200101 & 108.30000000000000 \\ \hline 20200201 & 108.60000000000000 \\ \hline 20200301 & 108.60000000000000 \\ \hline 20200401 & 108.60000000000000 \\ \hline 20200501 & 108.60000000000000 \\ \hline 20200601 & 108.80000000000000 \\ \hline 20200701 & 109.20000000000000 \\ \hline 20200801 & 108.80000000000000 \\ \hline 20200901 & 109.20000000000000 \\ \hline 20201001 & 109.20000000000000 \\ \hline 20201101 & 109.10000000000000 \\ \hline 20201201 & 109.40000000000000 \\ \hline 20210101 & 109.30000000000000 \\ \hline 20210201 & 109.40000000000000 \\ \hline 20210301 & 109.70000000000000 \\ \hline 20210401 & 110.40000000000000 \\ \hline 20210501 & 111.00000000000000 \\ \hline 20210601 & 111.40000000000000 \\ \hline 20210701 & 111.40000000000000 \\ \hline 20210801 & 112.10000000000000 \\ \hline 20210901 & 112.40000000000000 \\ \hline 20211001 & 113.40000000000000 \\ \hline 20211101 & 114.10000000000000 \\ \hline 20211201 & 114.70000000000000 \\ \hline 20220101 & 114.60000000000000 \\ \hline 20220201 & 115.40000000000000 \\ \hline 2020301 & 116.50000000000000 \\ \hline 20201 & 119.00000000000000 \\ \hline 2001 & 119.70000000000000 \\ \hline \hline - & 120.50000000000000 \\ \hline 201 & 121.20000000000000 \\ \hline \end{tabular}