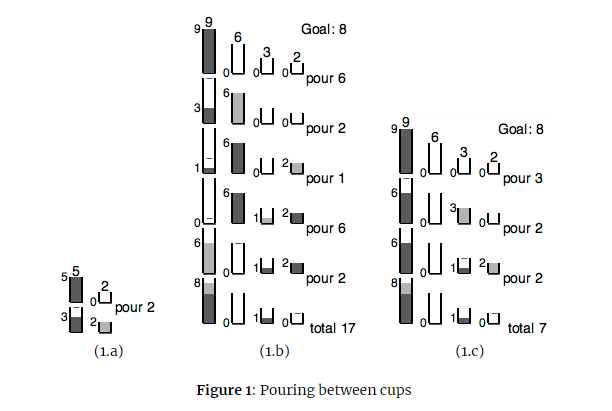
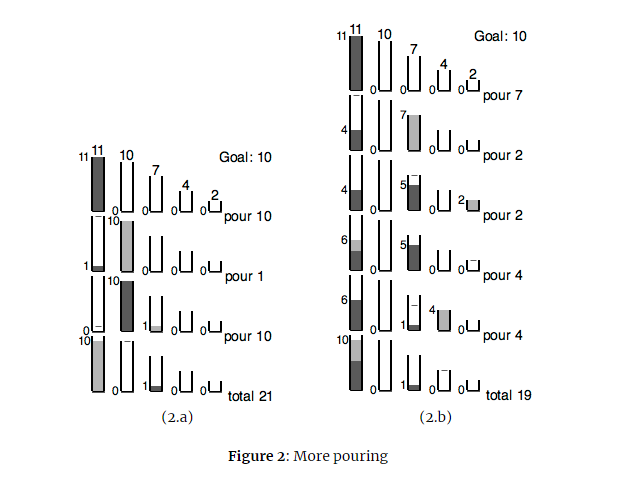
You are making a recipe and need to measure a precise volume of liquid. There are an assortment of cups of varying volumes in your kitchen, however no cup has any markings on it other than to indicate its total volume, and none of them match the volume that you want. You start with the biggest cup full of liquid and, to make sure you know precisely how much volume you are working with at any point in time, you consider steps in which you pour from any nonempty cup into another cup, always pouring until either the cup you are pouring into becomes full, or the cup you are pouring from becomes empty (whichever occurs first). As a simple example, assume you start with a full cup having capacity 55, and you have another cup with capacity 22, but your goal is to have 33 units of the liquid in the largest cup. In this case, you can start pouring from the larger cup to the smaller, stopping when the smaller one reaches its capacity of 22. This will leave precisely 33 units in the larger cup. See Figure 1(a). As another example, consider a case in which you have 44 cups with capacities 99, 66, 33, and 22, and you start with the largest cup full, the rest empty, and a goal of ending with 88 units in the largest cup. For ease of discussion we will refer to the cup with capacity 99 as the 99-cup and similarly for the other sizes. You notice that the 66-cup and 22-cup have combined capacity of 88, and so you could pour from the original 99-cup to fill those two cups, then dump the remaining 11 unit from the 99-cup into the 33-cup, and finally pour the full 66-cup and 22-cup back into the 99-cup. See Figure 1(b). In implementing this strategy, the total volume of liquid poured would be 6+2+1+6+2=176+2+1+6+2=17. You could achieve this goal in another way: pour 33 units from the 99-cup to the 33-cup (leaving 66 units in the 99-cup), then fill the 22-cup from the 33-cup (leaving 11 unit in the 22 cup), and finally pour the full 22-cup back into the 99-cup, resulting in exactly 88 units in that cup. With this strategy, the total volume poured is only 3+2+2=73+2+2=7. See Figure 1(c). As a final example, you start with cups of capacities 1111, 1010, 77, 44, and 22, with the 1111-cup full, and a goal of ending up with 1010 units in the 1111-cup. Obviously, you could fill the 1010-cup, dump the remaining 11 unit into another cup, and then pour from the full 1010-cup back into the 1111-cup, as illustrated in Figure 2(a). These three pours would mean transferring a total volume of 10+1+10=2110+1+10=21. Figure 2(b) shows a sequence with more steps, but less liquid poured. Input The input consists of a single line of positive integers: nn c1c1 c2c2 cncn VV, where there are nn cups, with 2n52n5, having capacities satisfying 64c1>c2>>cn164c1>c2>>cn1. The value Vlargest cup. Output Output the minimum amount of liquid that must be poured to achieve the goal, or output impossible if the goal cannot be achieved. Sample Input 1 Sample Output 1 2 5 2 3 2 Sample Input 2 Sample Output 2 4 9 6 3 2 8 7 Sample Input 3 Sample Output 3 5 11 10 7 4 2 10 19 Sample Input 4 Sample Output 4 2 5 2 4 impossible Goal: 8 6 pour 6 L pour 2 Goal: 8 pour 1 pour 3 [] pour 6 pour 2 5 p11 111 10 Goal: 10 pour 7 11.11 10 Goal: 10 pour 2 || [1] * \\\ : 4 Sample Input 5 Sample Output 5 5 64 45 41 28 2 63 121

Explain how Dijkstra's algorithm can be used to solve this problem. Since no graph is described explicitly in the problem, describe the graph that Dijkstra's algorithm is applied to and how its nodes and edges are generated.

Goal: 8 6 pour 6 L pour 2 Goal: 8 pour 1 pour 3 [] pour 6 pour 2 5 pour 2 pour 2 pour 2 L, total 17 total 7 (1.a) (1.b) (1.c) Figure 1: Pouring between cups 11 111 10 Goal: 10 pour 7 11.11 10 Goal: 10 pour 2 || [1] * \\\ : 4 \\ pour 10 pour 2 6 10 pour 1 pour 4 1 1 .1 101 pour 10 pour 4 || | "|||| total 21 total 19 (2.a) (2.b) Figure 2: More pouring Goal: 8 6 pour 6 L pour 2 Goal: 8 pour 1 pour 3 [] pour 6 pour 2 5 pour 2 pour 2 pour 2 L, total 17 total 7 (1.a) (1.b) (1.c) Figure 1: Pouring between cups 11 111 10 Goal: 10 pour 7 11.11 10 Goal: 10 pour 2 || [1] * \\\ : 4 \\ pour 10 pour 2 6 10 pour 1 pour 4 1 1 .1 101 pour 10 pour 4 || | "|||| total 21 total 19 (2.a) (2.b) Figure 2: More pouring