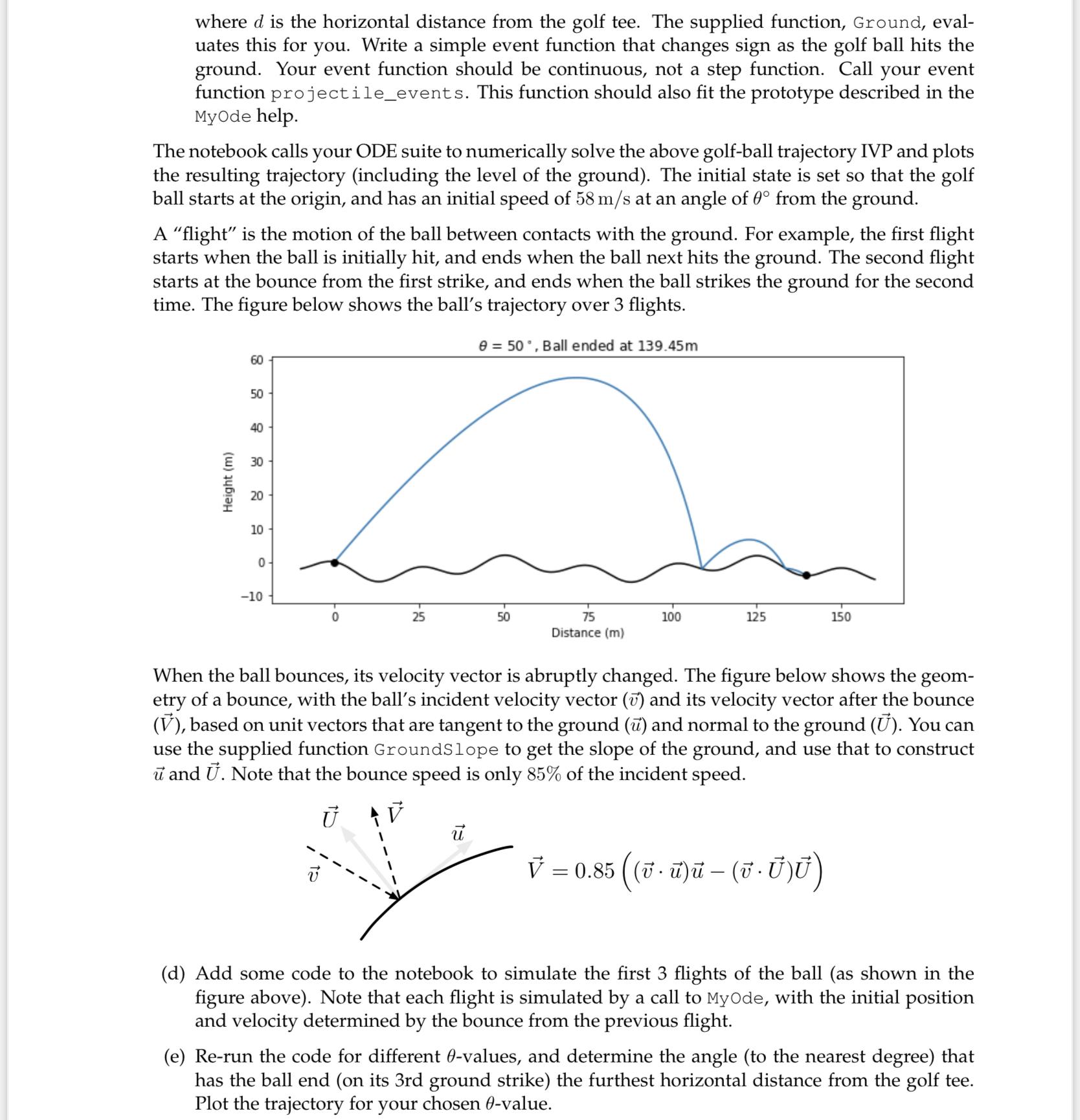
You are taking part in a golf driving-range competition to see who can hit the ball farthest. The distance that counts is where the ball lands on its third bounce. In this task, you will write your own ODE solving suite that performs Modified Euler (also known as Improved Euler) time stepping, and use the suite to solve for the trajectory of a golf ball, ac- counting for air resistance. The system of differential equations that governs the motion of a pro- jectile, like a golf ball, is x"(t) = -K x' (t) y"(t)-g-K y' (t), = where g is 9.81 m/s, and K is a coefficient of air resistance. You may assume that K always equals 0.3 for this task. (a) Complete the Python function Myode, t, y = Myode (de, tspan, y0, h, event) that numerically solves the IVP using Modified Euler time stepping using a fixed time step of h. See the help documentation in the supplied code for an explanation of the input and output variables. Importantly, your function should ignore the event function for the first time step. Note that if Myode detects the occurrence of an event, it should linearly interpolate between the last two points to find a more accurate estimate for the time of the event. Then it should interpolate the state at that new, interpolated end time. (b) Formulate the system of ODEs above into a first order system, and create a Python function called projectile that fits the prototype of the dynamics function described in the Myode help. (c) The driving range has rolling hills, so that the level of the ground is a cosine function, = 2 (cos (1) - () - sin (1)-) Ground (d) = 2 ( cos where d is the horizontal distance from the golf tee. The supplied function, Ground, eval- uates this for you. Write a simple event function that changes sign as the golf ball hits the ground. Your event function should be continuous, not a step function. Call your event function projectile_events. This function should also fit the prototype described in the Myode help. The notebook calls your ODE suite to numerically solve the above golf-ball trajectory IVP and plots the resulting trajectory (including the level of the ground). The initial state is set so that the golf ball starts at the origin, and has an initial speed of 58 m/s at an angle of 0 from the ground. A "flight" is the motion of the ball between contacts with the ground. For example, the first flight starts when the ball is initially hit, and ends when the ball next hits the ground. The second flight starts at the bounce from the first strike, and ends when the ball strikes the ground for the second time. The figure below shows the ball's trajectory over 3 flights. 0 = 50, Ball ended at 139.45m Height (m) 60 50 40 30 20 10 0- -10 25 50 U 75 Distance (m) 100 125 150 When the ball bounces, its velocity vector is abruptly changed. The figure below shows the geom- etry of a bounce, with the ball's incident velocity vector (7) and its velocity vector after the bounce (V), based on unit vectors that are tangent to the ground () and normal to the ground (). You can use the supplied function GroundSlope to get the slope of the ground, and use that to construct u and U. Note that the bounce speed is only 85% of the incident speed. 1 = 0.85 ((v ) (v )) (d) Add some code to the notebook to simulate the first 3 flights of the ball (as shown in the figure above). Note that each flight is simulated by a call to Myode, with the initial position and velocity determined by the bounce from the previous flight. (e) Re-run the code for different 0-values, and determine the angle (to the nearest degree) that has the ball end (on its 3rd ground strike) the furthest horizontal distance from the golf tee. Plot the trajectory for your chosen (-value.