Question: You are to complete two features: tree traversal and avl balance (right and left) rotations. Look for Fill the blank block comment as shown below:
You are to complete two features:
tree traversal and
avl balance (right and left) rotations.
Look for Fill the blank block comment as shown below:
// // fill the blank //
Test Run Example
Submit a test run screenshot using the test pattern below:
string input = "h,d,l,b,f,j,n,a,c,e,g,i,k,m,o";
Then test the 3 different traversal.
This is what the ouput looks right now:
Create a default AVLtree (BST) (after completion of this assignment, this should be an AVL Tree): Display the binary search tree as it is being built: +-- h +-- h +-- d +-- l +-- h +-- d +-- l +-- h +-- d +-- b +-- l +-- h | +-- f +-- d +-- b +-- l | +-- j +-- h | +-- f +-- d +-- b +-- n +-- l | +-- j +-- h | +-- f +-- d +-- b +-- n +-- l | +-- j +-- h | +-- f +-- d +-- b +-- a +-- n +-- l | +-- j +-- h | +-- f +-- d | +-- c +-- b +-- a +-- n +-- l | +-- j +-- h | +-- f | | +-- e +-- d | +-- c +-- b +-- a +-- n +-- l | +-- j +-- h | +-- g | +-- f | | +-- e +-- d | +-- c +-- b +-- a +-- n +-- l | +-- j | +-- i +-- h | +-- g | +-- f | | +-- e +-- d | +-- c +-- b +-- a +-- n +-- l | | +-- k | +-- j | +-- i +-- h | +-- g | +-- f | | +-- e +-- d | +-- c +-- b +-- a +-- n | +-- m +-- l | | +-- k | +-- j | +-- i +-- h | +-- g | +-- f | | +-- e +-- d | +-- c +-- b +-- a +-- o +-- n | +-- m +-- l | | +-- k | +-- j | +-- i +-- h | +-- g | +-- f | | +-- e +-- d | +-- c +-- b +-- a +-- o +-- n | +-- m +-- l | | +-- k | +-- j | +-- i +-- h | +-- g | +-- f | | +-- e +-- d | +-- c +-- b +-- a ====BINARY SEARCH TREE MENU==== Delimiter is (,) t - TOGGLE trace: (OFF) LEVEL-0 p - PRINT tree e - isEMPTY? h - getHEIGHT n - NUMBER of Nodes b - BUILD tree from a node list i - INSERT r - REMOVE c - CLEAR 1 - In Order Traversal 2 - Pre Order Traversal 3 - Post Order Traversal m - MENU - this menu q - quit this menu TRACE_level_0 -->YOUR CHOICE->
The output below is what I need after the fill in the blank part.

The purpose of this assignment is to become familiar with a standard approach in the self-balancing implementation of the C++ binary search tree.
There are four blanked out code segments are:
1. Line 326 BinaryNodeTree class, traversal methods: preorder() and postorder()
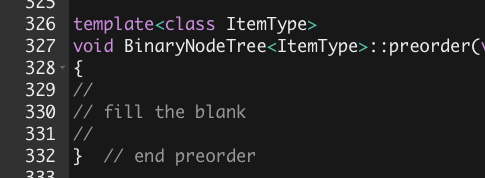
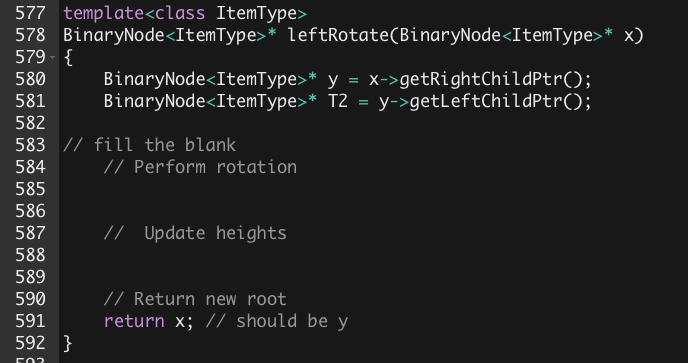
2. Line 577 AVLtree class leftRotate() method
Make sure change line 591 back to
return y;
*The changing of return was to prevent certain unexpected effect for starter run.
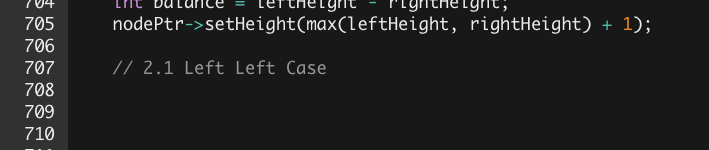
3. Line 707, of theAVLtree class removeNode method(), the four AVL rotation utilities: R-R, R-L, L-R, and L-L rotations.
Practically, all fill the blank code segment is appear multiple times in this file, you should be able to extract the proper working code when you get familiar with this AVLtree.h file.
When completed, make sure your validation contains:
the traversals, and
sequence of insertions and deletions.
AVLtree.h
#ifndef AVL_TREE
#define AVL_TREE
#include
#include
#include
//////////////////////
// BinaryNode
//////////////////////
template
class BinaryNode
{
private:
ItemType item; // Data portion
BinaryNode* leftChildPtr; // Pointer to left child
BinaryNode* rightChildPtr; // Pointer to right child
int height; // required by an AVL Tree Node
public:
BinaryNode()
: item(nullptr), leftChildPtr(nullptr), rightChildPtr(nullptr), height(1) {}
BinaryNode(const ItemType& anItem)
:item(anItem), leftChildPtr(nullptr), rightChildPtr(nullptr), height(1) {}
BinaryNode(const ItemType& anItem,
BinaryNode* leftPtr,
BinaryNode* rightPtr)
: item(anItem), leftChildPtr(leftPtr), rightChildPtr(rightPtr), height(1) {}
void setItem(const ItemType& anItem) {item = anItem;}
ItemType getItem() const {return item;}
bool isLeaf() const {
return ((leftChildPtr == nullptr) && (rightChildPtr == nullptr));
}
BinaryNode* getLeftChildPtr() const {return leftChildPtr;}
BinaryNode* getRightChildPtr() const {return rightChildPtr;}
void setLeftChildPtr(BinaryNode* leftPtr) {leftChildPtr = leftPtr;}
void setRightChildPtr(BinaryNode* rightPtr) {rightChildPtr = rightPtr;}
void drawTree(BinaryNode* , std::string , std::string) const;
int getHeight() const {return height;}
void setHeight(int h) {height = h;}
}; // end BinaryNode
////////////////////////////
// BinaryNodeTree Class
////////////////////////////
template
class BinaryNodeTree
{
private:
BinaryNode* rootPtr;
protected:
//------------------------------------------------------------
// Protected Utility Methods Section:
// Recursive helper methods for the public methods.
//------------------------------------------------------------
int getHeightHelper(BinaryNode* subTreePtr) const;
int getNumberOfNodesHelper(BinaryNode* subTreePtr) const ;
// Recursively deletes all nodes from the tree.
void destroyTree(BinaryNode* subTreePtr);
// Recursively adds a new node to the tree in a left/right fashion to
// keep the tree balanced.
BinaryNode* balancedAdd(BinaryNode* subTreePtr,
BinaryNode* newNodePtr);
// Removes the target value from the tree by calling moveValuesUpTree
// to overwrite value with value from child.
BinaryNode* removeValue(BinaryNode* subTreePtr,
const ItemType target,
bool& success);
// Copies values up the tree to overwrite value in current node until
// a leaf is reached; the leaf is then removed, since its value is
// stored in the parent.
BinaryNode* moveValuesUpTree(BinaryNode* subTreePtr);
// Recursively searches for target value in the tree by using a
// preorder traversal.
BinaryNode* findNode(BinaryNode* treePtr,
const ItemType& target,
bool& success) const;
// Copies the tree rooted at treePtr and returns a pointer to
// the copy.
BinaryNode* copyTree(const BinaryNode* treePtr) const;
// Recursive traversal helper methods:
void preorder(void visit(ItemType&), BinaryNode* treePtr) const;
void inorder(void visit(ItemType&), BinaryNode* treePtr) const;
void postorder(void visit(ItemType&), BinaryNode* treePtr) const;
public:
//------------------------------------------------------------
// Constructor and Destructor Section.
//------------------------------------------------------------
BinaryNodeTree() : rootPtr(nullptr) {}
BinaryNodeTree(const ItemType& rootItem) {
rootPtr = new BinaryNode(rootItem, nullptr, nullptr);
}
BinaryNodeTree(const ItemType& rootItem,
const BinaryNodeTree* leftTreePtr,
const BinaryNodeTree* rightTreePtr) {
rootPtr = new BinaryNode(rootItem,
copyTree(leftTreePtr->rootPtr),
copyTree(rightTreePtr->rootPtr));
}
BinaryNodeTree(const BinaryNodeTree& tree) {
rootPtr = copyTree(tree.rootPtr);
}
virtual ~BinaryNodeTree() {destroyTree(rootPtr);}
//------------------------------------------------------------
// Public BinaryTreeInterface Methods Section.
//------------------------------------------------------------
bool isEmpty() const {return rootPtr == nullptr;}
int getHeight() const {return getHeightHelper(rootPtr);}
int getNumberOfNodes() const {
return getNumberOfNodesHelper(rootPtr);
}
ItemType getRootData() const;
void setRootData(const ItemType& newData);
bool add(const ItemType& newData); // Adds a node
bool remove(const ItemType& data); // Removes a node
void clear() {destroyTree(rootPtr);rootPtr = nullptr;}
ItemType getEntry(const ItemType& anEntry) const;
bool contains(const ItemType& anEntry) const;
void drawTree(BinaryNode* treePtr, std::string lpad, std::string rpad) const;
//------------------------------------------------------------
// Public Traversals Section.
//------------------------------------------------------------
void preorderTraverse(void visit(ItemType&)) const {
preorder(visit, rootPtr);
}
void inorderTraverse(void visit(ItemType&)) const {
inorder(visit, rootPtr);
}
void postorderTraverse(void visit(ItemType&)) const {
postorder(visit, rootPtr);
}
//------------------------------------------------------------
// Overloaded Operator Section.
//------------------------------------------------------------
BinaryNodeTree& operator=(const BinaryNodeTree& rightHandSide);
}; // end BinaryNodeTree
//////////////////////////////////////////////////////////////
// Protected Utility Methods Section
//////////////////////////////////////////////////////////////
template
int BinaryNodeTree::getHeightHelper(BinaryNode* subTreePtr) const
{
if (subTreePtr == nullptr)
return 0;
else
return 1 + std::max(getHeightHelper(subTreePtr->getLeftChildPtr()),
getHeightHelper(subTreePtr->getRightChildPtr()));
} // end getHeightHelper
template
int BinaryNodeTree::getNumberOfNodesHelper(BinaryNode* subTreePtr) const
{
if (subTreePtr == nullptr)
return 0;
else
return 1 + getNumberOfNodesHelper(subTreePtr->getLeftChildPtr())
+ getNumberOfNodesHelper(subTreePtr->getRightChildPtr());
} // end getNumberOfNodesHelper
template
BinaryNode* BinaryNodeTree::balancedAdd(BinaryNode* subTreePtr,
BinaryNode* newNodePtr)
{
if (subTreePtr == nullptr)
return newNodePtr;
else
{
BinaryNode* leftPtr = subTreePtr->getLeftChildPtr();
BinaryNode* rightPtr = subTreePtr->getRightChildPtr();
if (getHeightHelper(leftPtr) > getHeightHelper(rightPtr))
{
rightPtr = balancedAdd(rightPtr , newNodePtr);
subTreePtr->setRightChildPtr(rightPtr );
}
else
{
leftPtr = balancedAdd(leftPtr, newNodePtr);
subTreePtr->setLeftChildPtr(leftPtr);
} // end if
return subTreePtr;
} // end if
} // end balancedAdd
template
BinaryNode* BinaryNodeTree::moveValuesUpTree(BinaryNode* subTreePtr)
{
BinaryNode* leftPtr = subTreePtr->getLeftChildPtr();
BinaryNode* rightPtr = subTreePtr->getRightChildPtr();
int leftHeight = getHeightHelper(leftPtr);
int rightHeight = getHeightHelper(rightPtr);
if (leftHeight > rightHeight)
{
subTreePtr->setItem(leftPtr->getItem());
leftPtr = moveValuesUpTree(leftPtr);
subTreePtr->setLeftChildPtr(leftPtr);
return subTreePtr;
}
else
{
if (rightPtr != nullptr)
{
subTreePtr->setItem(rightPtr->getItem());
rightPtr =moveValuesUpTree(rightPtr);
subTreePtr->setRightChildPtr(rightPtr);
return subTreePtr;
}
else
{
//this was a leaf!
// value not important
delete subTreePtr;
return nullptr;
} // end if
} // end if
} // end moveValuesUpTree
/** Depth-first search of tree for item.
@param subTreePtr tree to search.
@param target target item to find.
@param success communicate to client we found it.
@returns A pointer to node containing the item. */
template
BinaryNode* BinaryNodeTree::removeValue(BinaryNode* subTreePtr,
const ItemType target,
bool& success)
{
if(subTreePtr == nullptr) // not found here
return nullptr;
if (subTreePtr->getItem() == target) // found it
{
subTreePtr = moveValuesUpTree(subTreePtr);
success = true;
return subTreePtr;
}
else
{
BinaryNode* targetNodePtr = removeValue(subTreePtr->getLeftChildPtr(), target, success);
subTreePtr->setLeftChildPtr(targetNodePtr);
if (!success) // no need to search right subTree
{
targetNodePtr = removeValue(subTreePtr->getRightChildPtr(), target, success);
subTreePtr->setRightChildPtr(targetNodePtr);
} // end if
return subTreePtr;
} // end if
} // end removeValue
template
BinaryNode* BinaryNodeTree::findNode(BinaryNode* treePtr,
const ItemType& target,
bool& success) const
{
if (treePtr == nullptr) // not found here
return nullptr;
if (treePtr->getItem() == target) // found it
{
success = true;
return treePtr;
}
else
{
BinaryNode* targetNodePtr = findNode(treePtr->getLeftChildPtr(), target, success);
if (!success) // no need to search right subTree
{
targetNodePtr = findNode(treePtr->getRightChildPtr(), target, success);
} // end if
return targetNodePtr;
} // end if
} // end findNode
template
BinaryNode* BinaryNodeTree::copyTree(const BinaryNode* treePtr) const
{
BinaryNode* newTreePtr = nullptr;
// Copy tree nodes during a preorder traversal
if (treePtr != nullptr)
{
// Copy node
newTreePtr = new BinaryNode(treePtr->getItem(), nullptr, nullptr);
newTreePtr->setLeftChildPtr(copyTree(treePtr->getLeftChildPtr()));
newTreePtr->setRightChildPtr(copyTree(treePtr->getRightChildPtr()));
} // end if
return newTreePtr;
} // end copyTree
template
void BinaryNodeTree::destroyTree(BinaryNode* subTreePtr)
{
if (subTreePtr != nullptr)
{
destroyTree(subTreePtr->getLeftChildPtr());
destroyTree(subTreePtr->getRightChildPtr());
delete subTreePtr;
} // end if
} // end destroyTree
//////////////////////////////////////////////////////////////
// Protected Tree Traversal Sub-Section
//////////////////////////////////////////////////////////////
template
void BinaryNodeTree::preorder(void visit(ItemType&), BinaryNode* treePtr) const
{
//
// fill the blank
//
} // end preorder
template
void BinaryNodeTree::inorder(void visit(ItemType&), BinaryNode* treePtr) const
{
if(treePtr) {
inorder( visit, treePtr->getLeftChildPtr());
ItemType thisItem = treePtr->getItem();
visit(thisItem);
inorder( visit, treePtr->getRightChildPtr());
}
} // end inorder
template
void BinaryNodeTree::postorder(void visit(ItemType&), BinaryNode* treePtr) const
{
//
// fill the blank
//
} // end postorder
//////////////////////////////////////////////////////////////
// PUBLIC METHODS BEGIN HERE
//////////////////////////////////////////////////////////////
//////////////////////////////////////////////////////////////
// Public BinaryTreeInterface Methods Section
//////////////////////////////////////////////////////////////
template
ItemType BinaryNodeTree::getRootData() const
{
if (isEmpty())
std::cout
return rootPtr->getItem();
} // end getRootData
template
void BinaryNodeTree::setRootData(const ItemType& newItem)
{
if (isEmpty())
rootPtr = new BinaryNode(newItem, nullptr, nullptr);
else
rootPtr->setItem(newItem);
} // end setRootData
template
bool BinaryNodeTree::add(const ItemType& newData)
{
BinaryNode* newNodePtr = new BinaryNode(newData);
rootPtr = balancedAdd(rootPtr, newNodePtr);
return true;
} // end add
template
bool BinaryNodeTree::remove(const ItemType& target)
{
bool isSuccessful = false;
rootPtr = removeValue(rootPtr, target, isSuccessful);
return isSuccessful;
} // end remove
template
ItemType BinaryNodeTree::getEntry(const ItemType& anEntry) const
{
bool isSuccessful = false;
BinaryNode* binaryNodePtr = findNode(rootPtr, anEntry, isSuccessful);
if (isSuccessful)
return binaryNodePtr->getItem();
else
std::cout
} // end getEntry
template
bool BinaryNodeTree:: contains(const ItemType& anEntry) const
{
bool isSuccessful = false;
findNode(rootPtr, anEntry, isSuccessful);
return isSuccessful;
} // end contains
//////////////////////////////////////////////////////////////
// Public Traversals Section
//////////////////////////////////////////////////////////////
template
void BinaryNodeTree::drawTree(BinaryNode* treePtr, std::string lpad, std::string rpad) const
{
std::string pad = lpad.substr(0, lpad.size() - 1);
if (treePtr == nullptr) return;
drawTree(treePtr->getRightChildPtr(), rpad + " |", rpad + " ");
std::cout getItem()
drawTree(treePtr->getLeftChildPtr(), lpad + " ", lpad + " |");
} // end drawTree
//////////////////////////////////////////////////////////////
// Overloaded Operator
//////////////////////////////////////////////////////////////
template
BinaryNodeTree& BinaryNodeTree::
operator=(const BinaryNodeTree& rightHandSide)
{
if (!isEmpty())
clear();
this = copyTree(&rightHandSide);
return *this;
} // end operator=
//////////////////////////////
// AVLtree Class
//////////////////////////////
template
class AVLtree : public BinaryNodeTree
{
private:
BinaryNode* rootPtr;
int getHeight(BinaryNode* node);
int getBalance(BinaryNode* node);
protected:
ItemType findSuccessorValue(BinaryNode* subTreePtr);
//------------------------------------------------------------
// Protected Utility Methods Section:
// Recursive helper methods for the public methods.
//------------------------------------------------------------
// Recursively finds where the given node should be placed and
// inserts it in a leaf at that point.
BinaryNode* insertInorder(BinaryNode* subTreePtr,
BinaryNode* newNode);
// Removes the given target value from the tree while maintaining a
// binary search tree.
BinaryNode* removeValue(BinaryNode* subTreePtr,
const ItemType target,
bool& success);
// Removes a given node from a tree while maintaining a
// binary search tree.
BinaryNode* removeNode(BinaryNode* nodePtr);
// Removes the leftmost node in the left subtree of the node
// pointed to by nodePtr.
// Sets inorderSuccessor to the value in this node.
// Returns a pointer to the revised subtree.
BinaryNode* removeLeftmostNode(BinaryNode* subTreePtr,
ItemType& inorderSuccessor);
// Returns a pointer to the node containing the given value,
// or nullptr if not found.
BinaryNode* findNode(BinaryNode* treePtr,
const ItemType& target) const;
public:
//------------------------------------------------------------
// Constructor and Destructor Section.
//------------------------------------------------------------
AVLtree() : rootPtr(nullptr) {}
AVLtree(const ItemType& rootItem) {
rootPtr = new BinaryNode(rootItem, nullptr, nullptr);
}
AVLtree(const AVLtree& tree) {
rootPtr = this->copyTree(tree.rootPtr);
}
virtual ~AVLtree() {
this->destroyTree(rootPtr);
}
//------------------------------------------------------------
// Public Methods Section.
//------------------------------------------------------------
bool isEmpty() const { return rootPtr == nullptr; }
int getHeight() const { return this->getHeightHelper(rootPtr); }
int getNumberOfNodes() const { return this->getNumberOfNodesHelper(rootPtr); }
ItemType getRootData() const;
void setRootData(const ItemType& newData) const {
std::cout
}
bool add(const ItemType& newEntry);
bool remove(const ItemType& anEntry);
void clear() { this->destroyTree(rootPtr); rootPtr = nullptr; }
ItemType getEntry(const ItemType& anEntry) const;
// Override contains to use our improved findNode:
bool contains(const ItemType& anEntry) const {
return findNode(rootPtr, anEntry); // nullptr is same as false
}
//------------------------------------------------------------
// Public Traversals Section.
//------------------------------------------------------------
void preorderTraverse(void visit(ItemType&)) const { // Call inherited method
this->preorder(visit, rootPtr); // Call inherited method
}
void inorderTraverse(void visit(ItemType&)) const {
this->inorder(visit, rootPtr);
}
void postorderTraverse(void visit(ItemType&)) const {
this->postorder(visit, rootPtr);
}
void drawAVLtree() const;
//------------------------------------------------------------
// Overloaded Operator Section.
//------------------------------------------------------------
AVLtree& operator=(const AVLtree& rightHandSide);
}; // end AVLtree
////////////////////////////////////////////////////////////
// non-member public helper
int max(int a, int b) { return (a > b) ? a : b; }
template
int height(BinaryNode* nodePtr) {
if (nodePtr == NULL) return 0;
return nodePtr->getHeight();
}
//////////////////////////////////////////////////////////////
//
// Protected Utility Methods Section
//
//////////////////////////////////////////////////////////////
template
BinaryNode* rightRotate(BinaryNode* y)
{ // std::cout
BinaryNode* x = y->getLeftChildPtr();
BinaryNode* T2 = x->getRightChildPtr();
// Perform rotation
x->setRightChildPtr(y);
y->setLeftChildPtr(T2);
// Update heights
y->setHeight(max(height(y->getLeftChildPtr()), height(y->getRightChildPtr())) + 1);
x->setHeight(max(height(x->getLeftChildPtr()), height(x->getRightChildPtr())) + 1);
// Return new root
return y; // should be x
}
template
BinaryNode* leftRotate(BinaryNode* x)
{
BinaryNode* y = x->getRightChildPtr();
BinaryNode* T2 = y->getLeftChildPtr();
// Perform rotation
// Update heights
//
// fill the blank
//
// Return new root
return x; // should be y
}
template
BinaryNode* AVLtree
::insertInorder(BinaryNode* subTreePtr,
BinaryNode* newNodePtr)
{
if (subTreePtr == nullptr)
return newNodePtr;
else
{ // 1. Perform the normal BST insertion */
if (newNodePtr->getItem() getItem())
subTreePtr->setLeftChildPtr(insertInorder(subTreePtr->getLeftChildPtr(), newNodePtr));
else
subTreePtr->setRightChildPtr(insertInorder(subTreePtr->getRightChildPtr(), newNodePtr));
int leftHeight = getHeight(subTreePtr->getLeftChildPtr());
int rightHeight = getHeight(subTreePtr->getRightChildPtr());
// 2. Update height of this ancestor node
subTreePtr->setHeight(max(leftHeight, rightHeight) + 1);
// 3. Get the balance factor of this ancestor node to check whether this node became unbalanced
int balance = leftHeight - rightHeight;
BinaryNode* leftNode = subTreePtr->getLeftChildPtr();
BinaryNode* rightNode = subTreePtr->getRightChildPtr();
ItemType newKey = newNodePtr->getItem();
// If this node becomes unbalanced, then there are 4 cases
// 3.1 Left Left Case
if( balance > 1 && newKey getItem() ) return rightRotate(subTreePtr);
// 3.2 Right Right Case
if( balance rightNode->getItem() ) return leftRotate(subTreePtr);
// 3.3 Left Right Case
if (balance > 1 && newKey > leftNode->getItem()) {
subTreePtr->setLeftChildPtr(leftRotate(leftNode));
return rightRotate(subTreePtr); }
// 3.4 Right Left Case
if (balance getItem()) {
subTreePtr->setRightChildPtr(rightRotate(rightNode));
return leftRotate(subTreePtr); }
return subTreePtr;
} // end if
} // end AVL insertInorder()
template
int AVLtree::getHeight(BinaryNode* node)
{
if (node == nullptr) return 0;
return node->getHeight();
}
template
BinaryNode* AVLtree
::removeValue(BinaryNode* subTreePtr,
const ItemType target, bool& success) {
BinaryNode* nodePtr = subTreePtr;
// 1. Standard BST Deletion
if (subTreePtr == nullptr) { // Not found here
return nullptr;
}
if (subTreePtr->getItem() == target) {
success = true;
if (nodePtr->isLeaf()) {
delete nodePtr;
return (nodePtr = nullptr); // Assign and return (student maybe should have separate statements)
}
else if (nodePtr->getLeftChildPtr() == nullptr) { // Has rightChild only
BinaryNode* nodeToConnectPtr = nodePtr->getRightChildPtr();
delete nodePtr;
nodePtr = nullptr;
return nodeToConnectPtr;
}
else if (nodePtr->getRightChildPtr() == nullptr) { // Has left child only
BinaryNode* nodeToConnectPtr = nodePtr->getLeftChildPtr();
delete nodePtr;
nodePtr = nullptr;
return nodeToConnectPtr;
}
else { // Has two children
// Traditional way to remove a value in a node with two children
ItemType temp = findSuccessorValue(nodePtr->getRightChildPtr());
nodePtr->setItem(temp);
nodePtr->setRightChildPtr(removeValue(nodePtr->getRightChildPtr(), temp, success));
}
}
else {
if (subTreePtr->getItem() > target)
// Search the left subtree
subTreePtr->setLeftChildPtr(removeValue(subTreePtr->getLeftChildPtr(), target, success));
else
// Search the right subtree
subTreePtr->setRightChildPtr(removeValue(subTreePtr->getRightChildPtr(), target, success));
} // end if
// If only one node, return node
if (nodePtr == nullptr)
{
return nodePtr;
}
// 2. update height of current node and get balance
int leftHeight = getHeight(nodePtr->getLeftChildPtr());
int rightHeight = getHeight(nodePtr->getRightChildPtr());
int balance = leftHeight - rightHeight;
nodePtr->setHeight(max(leftHeight, rightHeight) + 1);
// 2.1 Left Left Case
// 2.2 right Right Case
// 2.3 Left Right Case
// 2.4 Right Left Case
return nodePtr;
} // end removeValue
template
BinaryNode* AVLtree
::removeNode(BinaryNode* nodePtr) {
// Case 1) Node is a leaf - it is deleted
// Case 2) Node has one child - parent adopts child
// Case 3) Node has two children:
// Traditional implementation: Find successor node.
// Alternate implementation: Find successor value and replace node's value;
// alternate does not need pass-by-reference
if (nodePtr->isLeaf()) {
delete nodePtr;
return (nodePtr = nullptr); // Assign and return (student maybe should have separate statements)
}
else if (nodePtr->getLeftChildPtr() == nullptr) { // Has rightChild only
BinaryNode* nodeToConnectPtr = nodePtr->getRightChildPtr();
delete nodePtr;
nodePtr = nullptr;
return nodeToConnectPtr;
}
else if (nodePtr->getRightChildPtr() == nullptr) { // Has left child only
BinaryNode* nodeToConnectPtr = nodePtr->getLeftChildPtr();
delete nodePtr;
nodePtr = nullptr;
return nodeToConnectPtr;
}
else { // Has two children
// Traditional way to remove a value in a node with two children
ItemType newNodeValue;
nodePtr->setRightChildPtr(removeLeftmostNode(nodePtr->getRightChildPtr(), newNodeValue));
nodePtr->setItem(newNodeValue);
return nodePtr;
}
} // end removeNode
template
int AVLtree::getBalance(BinaryNode* node)
{
if (node == nullptr)
{
return 0;
}
return height(node->getLeftChildPtr()) - height(node->getRightChildPtr());
}
template
BinaryNode* AVLtree
::removeLeftmostNode(BinaryNode* nodePtr,
ItemType& inorderSuccessor) {
if (nodePtr->getLeftChildPtr() == nullptr) {
inorderSuccessor = nodePtr->getItem();
return removeNode(nodePtr);
}
else {
nodePtr->setLeftChildPtr(removeLeftmostNode(nodePtr->getLeftChildPtr(), inorderSuccessor));
return nodePtr;
} // end if
} // end removeLeftmostNode
template
ItemType AVLtree::findSuccessorValue(BinaryNode* subTreePtr)
{
BinaryNode* myLeftChildPtr = subTreePtr->getLeftChildPtr();
if (myLeftChildPtr != nullptr)
{
if (myLeftChildPtr->getLeftChildPtr() == nullptr) {
ItemType nodeItemValue = myLeftChildPtr->getItem();
subTreePtr->setLeftChildPtr(removeNode(myLeftChildPtr));
return nodeItemValue;
}
else
{
return findSuccessorValue(subTreePtr->getLeftChildPtr());
} // end if
}
return subTreePtr->getItem();
} // end findSuccessorValue
// Override findNode because now we can use a binary search:
template
BinaryNode* AVLtree
::findNode(BinaryNode* subTreePtr,
const ItemType& target) const {
// Uses a binary search
if (subTreePtr == nullptr)
return nullptr; // Not found
else if (subTreePtr->getItem() == target)
return subTreePtr; // Found
else if (subTreePtr->getItem() > target)
// Search left subtree
return findNode(subTreePtr->getLeftChildPtr(), target);
else
// Search right subtree
return findNode(subTreePtr->getRightChildPtr(), target);
} // end findNode
//////////////////////////////////////////////////////////////
// Public BinaryTreeInterface Methods Section
//////////////////////////////////////////////////////////////
template
ItemType AVLtree::getRootData() const {
if (isEmpty())
std::cout
return rootPtr->getItem();
} // end getRootData
template
bool AVLtree::add(const ItemType& newData) {
BinaryNode* newNodePtr = new BinaryNode(newData);
rootPtr = insertInorder(rootPtr, newNodePtr);
return true;
} // end add
template
bool AVLtree::remove(const ItemType& target) {
bool isSuccessful = false;
rootPtr = removeValue(rootPtr, target, isSuccessful);
return isSuccessful;
} // end remove
// Override getEntry to use our improved findNode:
template
ItemType AVLtree::getEntry(const ItemType& anEntry) const {
BinaryNode* nodeWithEntry = findNode(rootPtr, anEntry);
if (nodeWithEntry == nullptr)
std::cout
else
return nodeWithEntry->getItem();
} // end getEntry
//////////////////////////////////////////////////////////////
// Public Traversals Section
//////////////////////////////////////////////////////////////
template
void AVLtree::drawAVLtree() const {
std::cout
this->drawTree(rootPtr, " ", " ");
std::cout
}
//////////////////////////////////////////////////////////////
// Overloaded Operator
//////////////////////////////////////////////////////////////
template
AVLtree& AVLtree::
operator=(const AVLtree& rightHandSide) {
if (!isEmpty())
clear();
this = copyTree(&rightHandSide); // Call inherited method
return *this;
} // end operator=
#endif
Running /home/ubuntu/workspace/consc?2 10/m88/testAv1.cpp Create a default AVLtree (BST (after completion of this assignment, this should be an AVL Tree): Display the binary search tree as it is being built: t-h tI1 0 rn +a +n +0 t-h 0 ?m ?a BINARY SEARCH TREE MENU Delimiter is(,) t TOGGLE trace: (OFF) LEVEL-0 p PRINT tree e - iSEMPTY h - getHEIGHT n -NUMBER of Nodes b-BUILD tree from a node list i - INSERT r -REMOVE C -CLEAR 1 In Order Traversal 2 -Pre Order Traversal 3 -Post Order Traversal mMENU -this menu q - quit this menu CE_level_0 >YOUR CHOICE-> 1 In-order traversal list: abcdefgh?jk1mnop RACE level 0 >YOUR CHOICE-2 re-order traversal list: jgdbacefh?n1knop RACE level 0 ->YOUR CHOICE-> 3 ost-order traversal list: acbfed?hgkmlpon TRACE level 0YOUR CHOICE- 17 Chern T Form 10. pdf psbjpeg Running /home/ubuntu/workspace/consc?2 10/m88/testAv1.cpp Create a default AVLtree (BST (after completion of this assignment, this should be an AVL Tree): Display the binary search tree as it is being built: t-h tI1 0 rn +a +n +0 t-h 0 ?m ?a BINARY SEARCH TREE MENU Delimiter is(,) t TOGGLE trace: (OFF) LEVEL-0 p PRINT tree e - iSEMPTY h - getHEIGHT n -NUMBER of Nodes b-BUILD tree from a node list i - INSERT r -REMOVE C -CLEAR 1 In Order Traversal 2 -Pre Order Traversal 3 -Post Order Traversal mMENU -this menu q - quit this menu CE_level_0 >YOUR CHOICE-> 1 In-order traversal list: abcdefgh?jk1mnop RACE level 0 >YOUR CHOICE-2 re-order traversal list: jgdbacefh?n1knop RACE level 0 ->YOUR CHOICE-> 3 ost-order traversal list: acbfed?hgkmlpon TRACE level 0YOUR CHOICE- 17 Chern T Form 10. pdf psbjpeg
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


