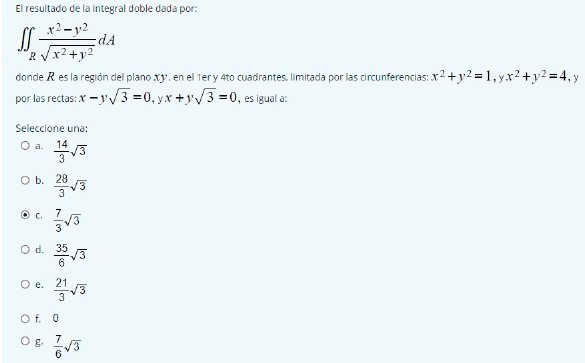
You can help me to solve the following double integral with change of variable and Jacobian if needed

The result of the integral given by

(x^2-y^2)/sqrt(x^+y^2)

where R is the region of the xy plane, in the first and fourth quadrants, bounded by the circles x^2+y^2=1, and x^2+y^2=4 and by the lines x-ysqrt(3)=0, and x+ysqrt(3) = 0, is equal to

a) (14/3)sqrt(3) b) (28/3)sqrt(3) c) (7/3)sqrt(3) d) (35/6)sqrt(3) e) (21/3)sqrt(3) f) 0 g) (7/6)sqrt(3)

El resultado de la integral doble dada por: x2-12 dA RVx-+v2 donde R es la region del plano xy', en el 1ery 4to cuadrantes, limitada por las circumferenceas: x2+ y?=1, yx2+ v2=4, y por las rectas: x -y:/ 3 =0, yx +y:/ 3 =0, es igual a: Seleccione una: O a 14 3 Ob. 28 3 7 O d. 35 6 De. 21 3 -/ 3 Of. 0 V3 6