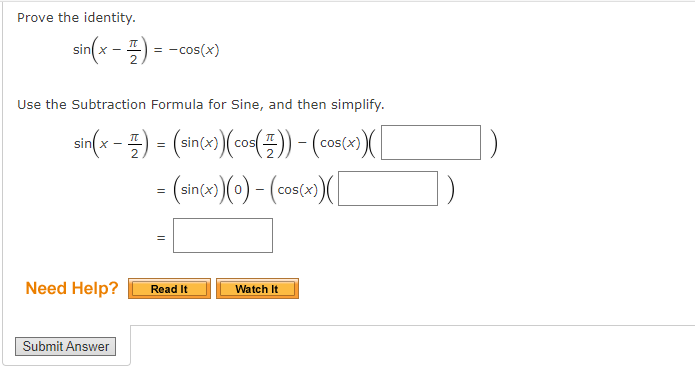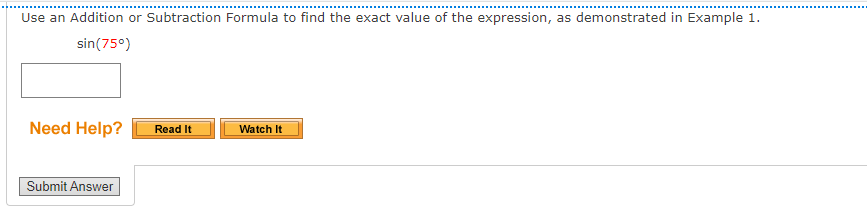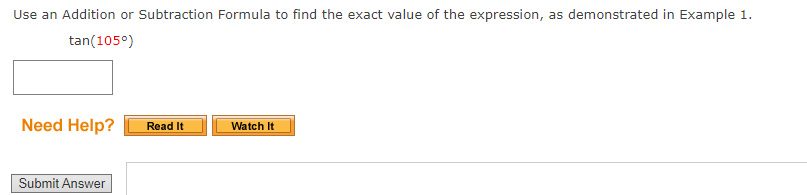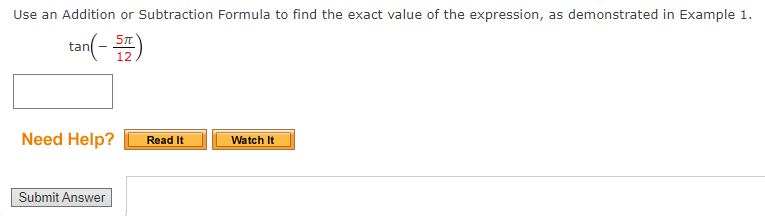
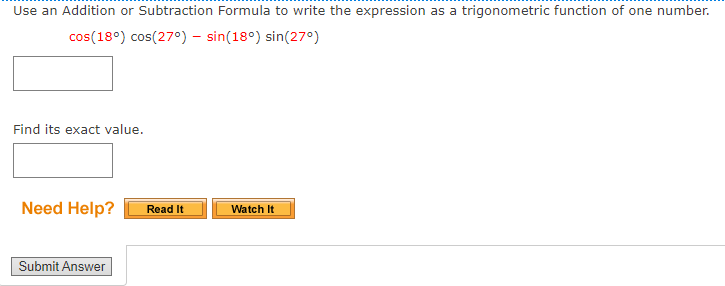
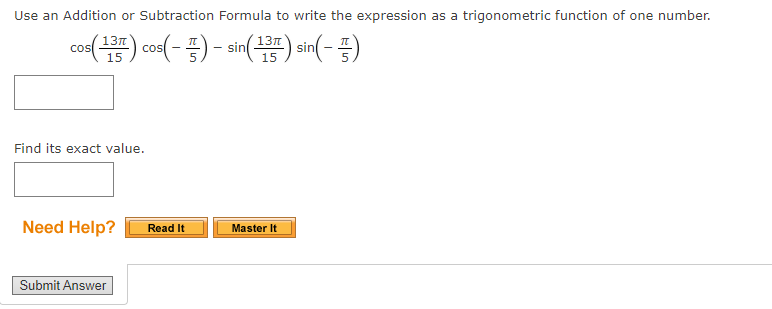

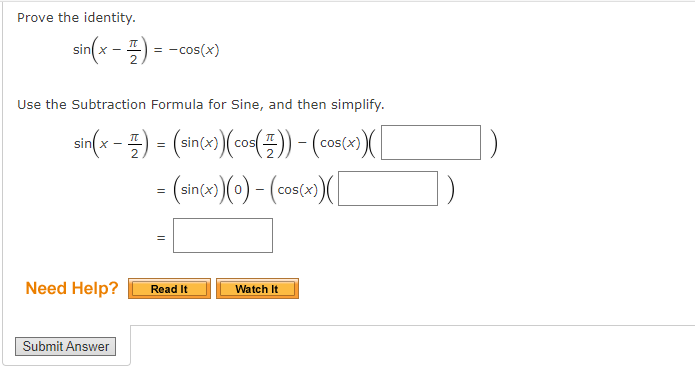
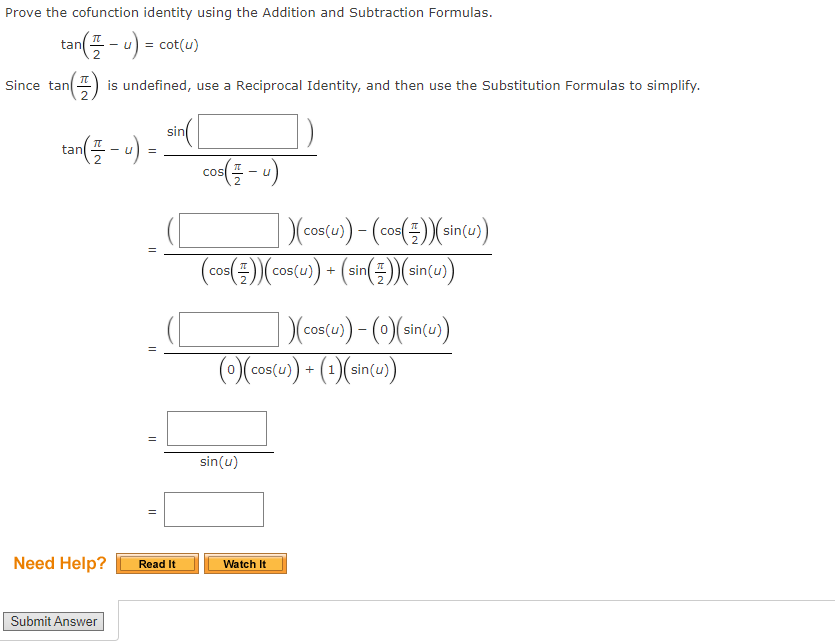
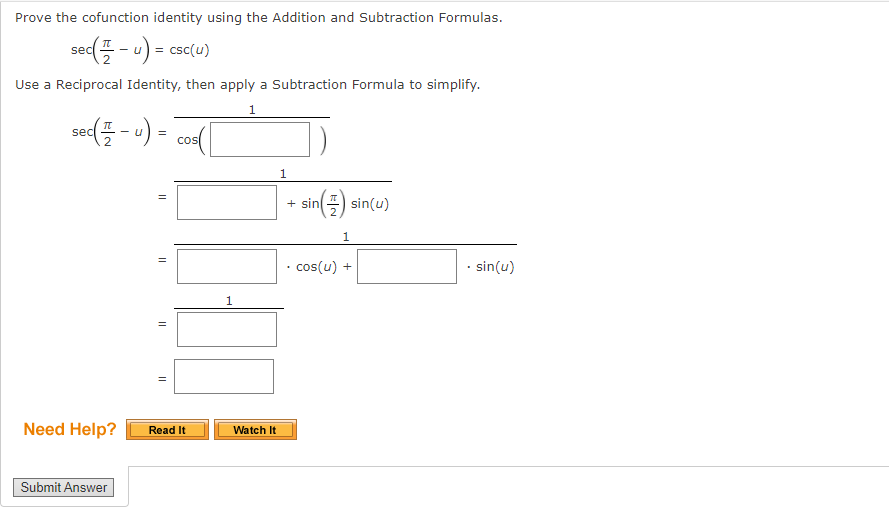
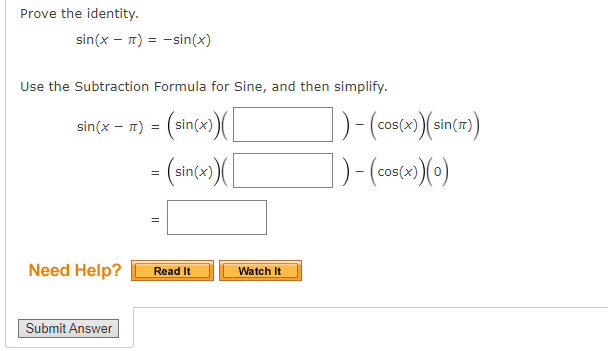
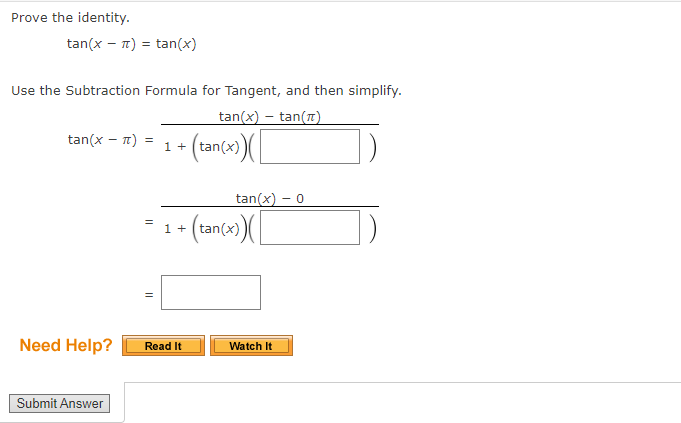
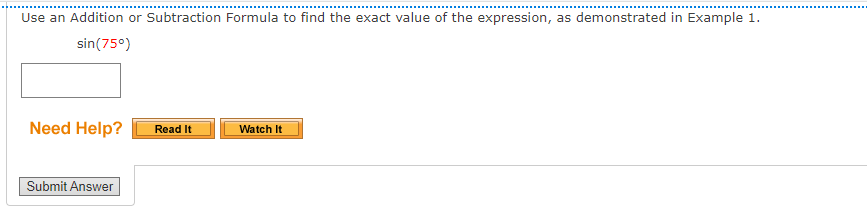


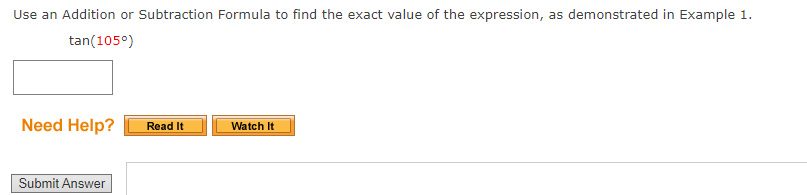


You dont have to show your work. You can circle the answer on the scratch work if you do have it.
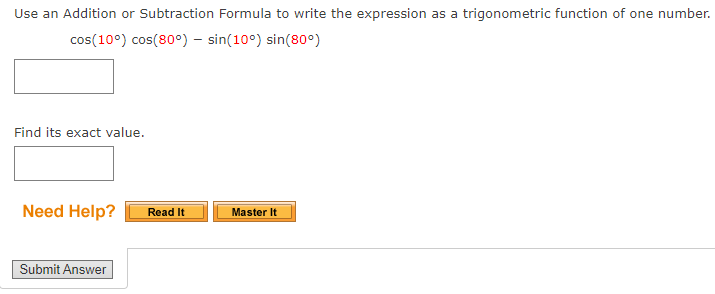
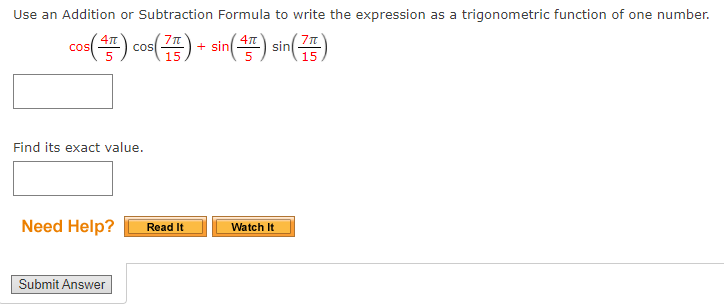
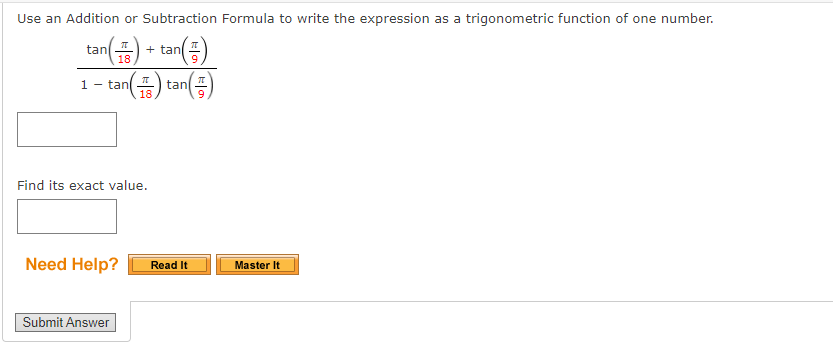
Use an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1. cos 29n 12 Need Help? Read It Submit AnswerUse an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1. tan( - 51 12 Need Help? Read It Watch It Submit AnswerUse an Addition or Subtraction Formula to write the expression as a trigonometric function of one number. cos(180) cos(270) - sin(180) sin(270) Find its exact value. Need Help? Read It Watch It Submit AnswerUse an Addition or Subtraction Formula to write the expression as a trigonometric function of one number. cos(109) cos(809) - sin(109) sin(80) Find its exact value. Need Help? Read It Master It Submit AnswerUse an Addition or Subtraction Formula to write the expression as a trigonometric function of one number. 4 1 COS COS + sin sin 5 15 5 15 Find its exact value. Need Help? Read It Watch It Submit AnswerUSe an Addition or Subtraction Formula to write the expression as a trigonometric function of one number. tan[i) + tan() 13 9 l tan(i)tan[1) 18 9 E Find its exact value. Z Need Help? Use an Addition or Subtraction Formula to write the expression as a trigonometric function of one number. cos (1327 ) cos(- ) - sin( 13:) sin( - Find its exact value. Need Help? Read It Master It Submit AnswerIf we know the values of the sine and cosine of x and y, we can find the value of sin(x - y) by using the ---Select--- |Formula for Sine. State the formula. sin (x - y) = Need Help? Read It Submit AnswerProve the identity. sin( x - = - cos(x) N Use the Subtraction Formula for Sine, and then simplify. sin(x - [) = (sin(x) ( cos ( # )) - (costx) ( = ( sin(x) (0) - cos(x) = Need Help? Read It Watch It Submit AnswerProve the cofunction identity using the Addition and Subtraction Formulas. tan( 1 - u) = cot(u) Since tan-) is undefined, use a Reciprocal Identity, and then use the Substitution Formulas to simplify. sin( tan = cos( 1 - u) ) ( cos ( U) ) - ( cos ( = ) ) ( sin ( u ) ) = cos( ) cos(U)) + (sin ()) ( sin(u) ) 1 ) (cos(4) - (0) ( sin(u)) (0) (cos( U) ) + (1 ) ( sin ( u ) ) = sin(u) = Need Help? Read It Watch It Submit AnswerProve the cofunction identity using the Addition and Subtraction Formulas. sec( 4 - u ) = csc(u) Use a Reciprocal Identity, then apply a Subtraction Formula to simplify. 1 sec 2 - U) = cos 1 + sin sin(u) . cos(U) + . sin(U) 1 = Need Help? Read It Watch It Submit AnswerProve the identity. sin(x - 7) = -sin(x) Use the Subtraction Formula for Sine, and then simplify. sin(x - n) = sin(x) - (cos(x)) (sin(It) = ( sin(x) )- (cos( x ) (0 ) Need Help? Read It Watch It Submit AnswerProve the identity. tan(x - 1) = tan(x) Use the Subtraction Formula for Tangent, and then simplify. tan(x) - tan(n) tan(x - ") = 1+ tan(x) tan(x) - 0 = 1+ tan(x) Need Help? Read It Watch It Submit AnswerUse an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1. sin(750) Need Help? Read It Watch It Submit AnswerUse an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1. sin (2850) Need Help? Read It Submit AnswerUse an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1. coS(1659) Need Help? Read It Submit AnswerUse an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1. tan (1050) Need Help? Read It Watch It Submit AnswerUse an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1. tan(2850) Need Help? Read It Submit AnswerUse an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1. sin 191 12 Need Help? Read It Watch It Submit