You must use pointers and functions in this C program. Please read the 5 page intructions and read the tips in the last page. Please write a simple code that will be understandable by beginner C-programmers. Please please provide relevant comments about how you did the code. Also when you need to use float, use %lf(long float) instead of just %f(float).

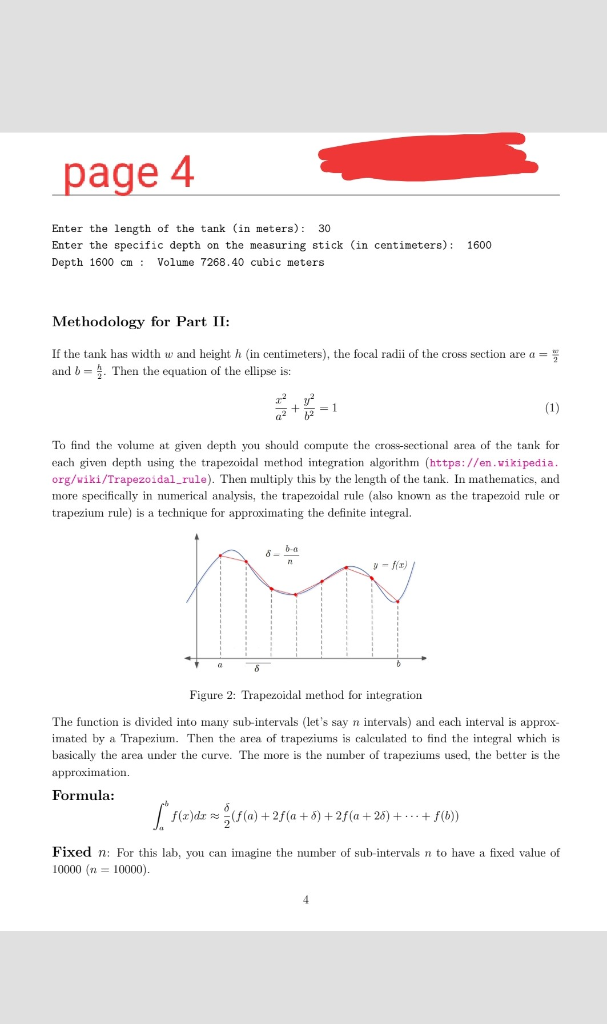
Functions and Pointers This lab will give you experience writing software that makes use of Functions and Pointers. Part I - Divisors Sum [4 points] In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible by another integer m if m is a divisor of n; this implies dividing n by m leaves no remainder. Now assume m and p are two divisors of n such that n=mxp, and let us call these two numbers "pair divisors of n. In part I, you are about to write a C program that receives an input number n and a query number q and checks if there is any "pair divisors of n that their sum is equal to the query number (checks whether q ==p+m). If there is any pair divisors, your code should return one of those pairs. The Code to be Written: 1. You are to write a C program, in a file called Lab5a.c 2. You must write a function that computes the pair divisors of n and returns one that their sum equals q (if there is any). This function is called by the main function and sets the pair values it finds via pointer addresses. This should be of the form of this prototype: void getPairDivisor(int n, int q, int* mAddress, int* pAddress) check to see that you used a C-language function, The variables mAddress and pAddress are the addresses to values of found p and m. Your algorithm should handle the cases where it does not find any result Your programs should work for any positive integer values of n, a (i.e. both n >1 and q> 1). Sample Outputs Please enter an input number n: 100 Please enter a query number q: 25 m = 5, p = 20, m*p = 100, and m+p = 25 page 2 Please enter an input number n: 77 Please enter a query number q: 18 m = 7, p = 11, m*p = 77, and m+p = 18 Please enter an input number n: 234 Please enter a query number q: 133 The program could not find any pair divisors for these inputs Part II - The Depth Guage Problem (6 points) Storage tanks are containers that hold liquids, compressed gases or mediums used for the short- or long-term storage of heat or cold. Storage tanks are available in many shapes: vertical and horizontal cylindrical; open top and closed top; flat bottom, cone bottom, slope bottom and dish bottom. Liquids are often stored in elliptical (cylindrical) storage tanks as shown in Figure 1. To measure the volume of liquid in the tank, a depth gauge (measuring stick) can be used. It is inserted into an opening at the top and the level of liquid on the gauge can be used to determine the amount of liquid in the tank. Imagine the tank has width w, height h and length len (all in meters). We look at inserting a measuring stick that is already calibrated in units of 10 centimeters. This measuring gauge can be inserted into an opening at the top of the tank and used to measure the depth of the liquid in the tank. For this part, your task will be to write a C program to compute a value for a specific depth showing the volume of liquid in the tank for that depth (e.g. 50cm or 370cm - always a multiplication of 10 centrimeters) Your programs should work for any values of w, h and len, and not just the specific values in the sample outputs below. We are assuming here that the user inputs valid numbers all the time. Sample Outputs page 3 Figure 1: Sample image for Part II. Enter the width of the tank (in meters): 8 Enter the height of the tank (in meters): 4 Enter the length of the tank (in meters): 7 Enter the specific depth on the measuring stick (in centimeters): 10 Depth 10.00 cm: Volume 1.17 cubic meters Enter the width of the tank (in meters): 5 Enter the height of the tank (in meters): 6 Enter the length of the tank (in meters): 7 Enter the specific depth on the measuring stick (in centimeters): 30 Depth 30 cm: Volume 3.08 cubic meters Enter the width of the tank (in meters): 9 Enter the height of the tank (in meters): 10 Enter the length of the tank (in meters): 12 Enter the specific depth on the measuring stick (in centimeters): 900 Depth 900 cm: Volume 804.02 cubic meters Enter the width of the tank (in meters): 18 Enter the height of the tank (in meters): 22 page 4 Enter the length of the tank (in meters): 30 Enter the specific depth on the measuring stick (in centimeters): 1600 Depth 1600 cm: Volume 7268.40 cubic meters Methodology for Part II: If the tank has width w and height h (in centimeters), the focal radii of the cross section are a = and b = . Then the equation of the ellipse is: To find the volume at given depth you should compute the cross-sectional area of the tank for each given depth using the trapezoidal method integration algorithm (https://en.wikipedia. org/wiki/Trapezoidal_rule). Then multiply this by the length of the tank. In mathematics, and more specifically in numerical analysis, the trapezoidal rule (also known as the trapezoid rule or trapezium rule) is a technique for approximating the definite integral. Figure 2: Trapezoidal method for integration The function is divided into many sub-intervals (let's say n intervals) and each interval is approx- imated by a Trapezium. Then the area of trapeziums is calculated to find the integral which is basically the area under the curve. under the curve. The more is the number of trapeziums used, the better is the approximation Formula: (f(a) +2f(a + ) +2f(a +26) + ... + f(6)) Fixed n: For this lab, you can imagine the number of sub-intervals n to have a fixed value of 10000 (n = 10000). page 5 Hint: It is probably easier to imagine the tank on its side so that the depth gauge is inserted horizontally. If you do this you must express the equation as a function of y and integrate that function. The Code to be Written: You must use a C 1. You are to write a C program, in a file called Lab5b.c 2. You must write a function that implements Equation 1. code 3. You must also write a function that compute the volume of the liquid using trapezoidal inte- gral and function you wrote for Equation 1. This should be of the form of this prototype: void trapezoidal_integral (double depth, int n, double width, double height, double length, double* integral result) Functions and Pointers This lab will give you experience writing software that makes use of Functions and Pointers. Part I - Divisors Sum [4 points] In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible by another integer m if m is a divisor of n; this implies dividing n by m leaves no remainder. Now assume m and p are two divisors of n such that n=mxp, and let us call these two numbers "pair divisors of n. In part I, you are about to write a C program that receives an input number n and a query number q and checks if there is any "pair divisors of n that their sum is equal to the query number (checks whether q ==p+m). If there is any pair divisors, your code should return one of those pairs. The Code to be Written: 1. You are to write a C program, in a file called Lab5a.c 2. You must write a function that computes the pair divisors of n and returns one that their sum equals q (if there is any). This function is called by the main function and sets the pair values it finds via pointer addresses. This should be of the form of this prototype: void getPairDivisor(int n, int q, int* mAddress, int* pAddress) check to see that you used a C-language function, The variables mAddress and pAddress are the addresses to values of found p and m. Your algorithm should handle the cases where it does not find any result Your programs should work for any positive integer values of n, a (i.e. both n >1 and q> 1). Sample Outputs Please enter an input number n: 100 Please enter a query number q: 25 m = 5, p = 20, m*p = 100, and m+p = 25 page 2 Please enter an input number n: 77 Please enter a query number q: 18 m = 7, p = 11, m*p = 77, and m+p = 18 Please enter an input number n: 234 Please enter a query number q: 133 The program could not find any pair divisors for these inputs Part II - The Depth Guage Problem (6 points) Storage tanks are containers that hold liquids, compressed gases or mediums used for the short- or long-term storage of heat or cold. Storage tanks are available in many shapes: vertical and horizontal cylindrical; open top and closed top; flat bottom, cone bottom, slope bottom and dish bottom. Liquids are often stored in elliptical (cylindrical) storage tanks as shown in Figure 1. To measure the volume of liquid in the tank, a depth gauge (measuring stick) can be used. It is inserted into an opening at the top and the level of liquid on the gauge can be used to determine the amount of liquid in the tank. Imagine the tank has width w, height h and length len (all in meters). We look at inserting a measuring stick that is already calibrated in units of 10 centimeters. This measuring gauge can be inserted into an opening at the top of the tank and used to measure the depth of the liquid in the tank. For this part, your task will be to write a C program to compute a value for a specific depth showing the volume of liquid in the tank for that depth (e.g. 50cm or 370cm - always a multiplication of 10 centrimeters) Your programs should work for any values of w, h and len, and not just the specific values in the sample outputs below. We are assuming here that the user inputs valid numbers all the time. Sample Outputs page 3 Figure 1: Sample image for Part II. Enter the width of the tank (in meters): 8 Enter the height of the tank (in meters): 4 Enter the length of the tank (in meters): 7 Enter the specific depth on the measuring stick (in centimeters): 10 Depth 10.00 cm: Volume 1.17 cubic meters Enter the width of the tank (in meters): 5 Enter the height of the tank (in meters): 6 Enter the length of the tank (in meters): 7 Enter the specific depth on the measuring stick (in centimeters): 30 Depth 30 cm: Volume 3.08 cubic meters Enter the width of the tank (in meters): 9 Enter the height of the tank (in meters): 10 Enter the length of the tank (in meters): 12 Enter the specific depth on the measuring stick (in centimeters): 900 Depth 900 cm: Volume 804.02 cubic meters Enter the width of the tank (in meters): 18 Enter the height of the tank (in meters): 22 page 4 Enter the length of the tank (in meters): 30 Enter the specific depth on the measuring stick (in centimeters): 1600 Depth 1600 cm: Volume 7268.40 cubic meters Methodology for Part II: If the tank has width w and height h (in centimeters), the focal radii of the cross section are a = and b = . Then the equation of the ellipse is: To find the volume at given depth you should compute the cross-sectional area of the tank for each given depth using the trapezoidal method integration algorithm (https://en.wikipedia. org/wiki/Trapezoidal_rule). Then multiply this by the length of the tank. In mathematics, and more specifically in numerical analysis, the trapezoidal rule (also known as the trapezoid rule or trapezium rule) is a technique for approximating the definite integral. Figure 2: Trapezoidal method for integration The function is divided into many sub-intervals (let's say n intervals) and each interval is approx- imated by a Trapezium. Then the area of trapeziums is calculated to find the integral which is basically the area under the curve. under the curve. The more is the number of trapeziums used, the better is the approximation Formula: (f(a) +2f(a + ) +2f(a +26) + ... + f(6)) Fixed n: For this lab, you can imagine the number of sub-intervals n to have a fixed value of 10000 (n = 10000). page 5 Hint: It is probably easier to imagine the tank on its side so that the depth gauge is inserted horizontally. If you do this you must express the equation as a function of y and integrate that function. The Code to be Written: You must use a C 1. You are to write a C program, in a file called Lab5b.c 2. You must write a function that implements Equation 1. code 3. You must also write a function that compute the volume of the liquid using trapezoidal inte- gral and function you wrote for Equation 1. This should be of the form of this prototype: void trapezoidal_integral (double depth, int n, double width, double height, double length, double* integral result)